Klassieke Mechanica/Statica

Inleiding

De statica is de studie van de voorwaarden die nodig zijn, opdat een voorwerp of een structuur in rust zou blijven. Voor een onvervormbaar voorwerp is vereist dat de versnelling en de hoekversnelling van het voorwerp beide nul zijn. Het is in feite een speciaal geval van de wet van Newton en de rotatiewet, namelijk een toestand waarbij de lineaire versnelling en de hoekversnelling beide nul zijn. Het is de gewoonte om de statica voor de dynamica te geven. Toch is het interessanter om eerst de hoofdstukken over elementaire dynamica en het eerste deel van de dynamica van voorwerpen, tot en met Rotatie rond as met vaste richting, door te nemen. Daardoor heeft men een veel beter idee van krachten en momenten en van de funderingen van de statica. De formules in de volgende paragraaf moeten dan niet intuïtief aangenomen worden, maar op basis van een wetenschappelijke fundering. Zie ook wat hierover gezegd wordt in de inleiding onder de titel Volgorde.

De voorwaarden voor statisch evenwicht kan men formuleren als:

• $\sum _{i}{\vec {F_{i}}}\,=\,0$
• $\sum _{i}{\vec {r}}_{Pi}\times {\vec {F_{i}}}\,=\,0$

met ${\vec {F_{i}}}$ de op het voorwerp of de structuur werkende krachten, P een willekeurig stilstaand punt (zie infra) en ${\vec {r}}_{Pi}$ de positievector van P naar het aangrijpingspunt van de kracht ${\vec {F_{i}}}$.

Dit is de vectoriële benadering. Voor een driedimensionaal systeem komen beide vectoriële vergelijkingen overeen met drie scalaire vergelijkingen. Bij een tweedimensionaal systeem leidt de eerste voorwaarde tot twee scalaire vergelijkingen. De momenten liggen dan alle volgens een as loodrecht op het vlak van de krachten en de posities. De momentenvoorwaarde leidt dan tot één scalaire vergelijking. Het tweedimensionale geval is dus veel eenvoudiger dan het driedimensionale. Bij een samengesteld systeem kan men met deze aanpak alle inwendige krachten tussen de onderdelen uitrekenen. Daarvoor moet het systeem opgesplitst worden in zijn onderdelen en moeten de evenwichtsvergelijkingen voor elk onderdeel opgeschreven worden.

Er is echter ook een andere benadering mogelijk. Deze vertrekt van de idee dat een versnelling van het systeem ook een toename of afname van de kinetische energie betekent. Dat kan alleen via een toevoer of afvoer van energie door de aangrijpende krachten. Geen versnelling betekent dus geen toevoer of afname van energie. Deze benadering leidt tot de methode van de virtuele arbeid. De energievergelijkingen zijn scalaire vergelijkingen. Daarom wordt deze methode soms de scalaire methode genoemd.

Met deze methode kunnen maar een beperkt aantal uitwendige krachten berekend worden. Ze is echter bijzonder geschikt om bij een complex mechanisme een verband te leggen tussen krachten op twee of meer punten van het systeem. Bij deze methode wordt het systeem een beetje bekeken als een black box. Men oefent er op één plaats een kracht op uit en de methode laat toe uit te rekenen welke kracht men op een andere plaats moet uitoefenen voor evenwicht, zonder dat men alle inwendige krachten moet berekenen. Zie bv. het voorbeeld van de ruitvormige krik aan het einde van het betrokken hoofdstuk. Ook laat de methode toe op een meer automatische manier de evenwichtsvergelijkingen op te stellen. Ze vormt de aanloop naar de methode van Lagrange, die de dynamische situatie (met lineaire en hoekversnelling) zal behandelen.

Evenwicht van een enkelvoudig onvervormbaar voorwerp

De evenwichtsvoorwaarde

De beweging van een onvervormbaar voorwerp kan altijd beschreven worden als een beweging van het massacentrum en een beweging t.o.v. het massacentrum. Voor een onvervormbaar voorwerp kan deze laatste beweging alleen maar een rotatie zijn. Een onvervormbaar voorwerp zal in rust zijn als het massacentrum niet beweegt en er geen rotatie is rond het massacentrum. Als er geen krachten werken op een voorwerp, zal het massacentrum zijn bewegingstoestand behouden, d.i. het zal in rust blijven of rechtlijnig verder bewegen met constante snelheid. Iets analoogs geldt voor de rotatiebeweging. De voorwaarden die men formuleert opdat een voorwerp in rust zou blijven, onderstellen in feite dat het voorwerp bij het aangrijpen van de gegeven krachten in rust is en zonder rotatie. In het hoofdstuk over de dynamica van voorwerpen wordt aangetoond dat

• $\sum _{i}{\vec {F_{i}}}\,=\,0$ nodig is opdat het massacentrum geen versnelling zou krijgen en het voorwerp dus in rust zou blijven;
• $\sum _{i}{\vec {r}}_{Ci}\times {\vec {F_{i}}}\,=\,0$ nodig is opdat het voorwerp geen hoekversnelling rond een as door het massacentrum zou krijgen en dus niet in rotatie zou komen. Hierbij is ${\vec {r}}_{Ci}$ de positievector van het aangrijpingspunt van de i-de kracht t.o.v. het massacentrum.

Wanneer het voorwerp in rust is, dan is het massacentrum een stilstaand punt. Als men het moment van de krachten uitrekent t.o.v. een ander stilstaand punt P, dan bestaat er een verband tussen beide momenten dat gegeven wordt door de verplaatsingsformule:
${\vec {\mu _{P}}}={\vec {\mu _{C}}}+{\vec {PC}}\times \sum _{i}{\vec {F_{i}}}$
Bij rust eist men echter dat de som van de krachten gelijk is aan 0, zodat het moment van alle krachten hetzelfde zal zijn t.o.v. om het even welk punt. Men kan dit moment dus ook uitrekenen t.o.v. de oorsprong van het assenkruis en men mag deze oorsprong om het even waar kiezen. Meestal wordt de evenwichtsvoorwaarde dan ook geformuleerd als:

$\quad \sum _{i}{\vec {F_{i}}}\,=\,0$
$\quad {\vec {\mu _{o}}}=\sum _{i}{\vec {r_{i}}}\times {\vec {F_{i}}}\,=\,0$

Praktische uitwerking

Het kan goed zijn om eens de tekst te herlezen over het vectorieel product en over de manieren om een moment uit te rekenen in het eerste hoofdstuk, in de topic Elementaire bewerkingen met vectoren.

In de praktijk moet men deze vergelijkingen projecteren op assen, voordat men getallen kan invullen. Voor een driedimensioneel probleem levert elke voorwaarde drie scalaire vergelijkingen, bv. door te projecteren op cartesische assen. De componenten van de kracht F_i worden daarbij geschreven met hoofdletters als X_i, Y_i en Z_i, en de coördinaten van het aangrijpingspunt met kleine letters als x_i, y_i en z_i. Men krijgt dan:
- som van de krachten = 0 levert:

• $\sum {X_{i}}=0$
  

• $\sum {Y_{i}}=0$
  

• $\sum {Z_{i}}=0$
  

- som van de momenten = 0 levert:

• $\sum {y_{i}.Z_{i}-z_{i}.Y_{i}}=0$
  

• $\sum {z_{i}.X_{i}-x_{i}.Z_{i}}=0$
  

• $\sum {x_{i}.Y_{i}-y_{i}.X_{i}}=0$
  

Voor een tweedimensionaal probleem blijven er maar drie vergelijkingen over:

• $\sum {X_{i}}=0$
• $\sum {Y_{i}}=0$

• $\sum {x_{i}.Y_{i}-y_{i}.X_{i}}=0$

Voorbeeld

schuin opgehangen balk

Een balk met gewicht G en lengte l is m.b.v. een scharnier en een kabel opgehangen onder een hoek van 30° met de horizontale. De kabel is onder een hoek van 60° met de verticale gespannen. Bereken de krachten in het scharnier en in de kabel.

Om dit probleem op te lossen moet men de balk bekijken en alle krachten die op de balk werken. Normaal raadt men aan om de balk afzonderlijk te tekenen, los van zijn omgeving. De situatie hier is echter nog eenvoudig genoeg om het bij één figuur te laten.

Uit de beschrijving blijkt dat de driehoek ABC gelijkzijdig is. De kracht in A heeft 2 componenten: X_A en Y_A. De spanning in het touw moet volgens het touw liggen (wordt later nog verklaard). Dit levert een schets op als op de figuur hiernaast. Er blijken 3 onbekenden in het probleem te zitten en men kan ook juist 3 vergelijkingen opschrijven. Het probleem is dus eenduidig bepaald.

De vergelijkingen worden:

$X_{A}-S.\cos {30^{o}}=0$

$Y_{A}+S.\sin 30^{o}-G=0$

De momentenvergelijking wordt opgeschreven t.o.v. het punt A, omdat dan de onbekende krachten in A niet voorkomen in die vergelijking. Men kan zo een vergelijking in één onbekende, nl. S, opstellen, die onmiddellijk kan opgelost worden:

$S.l.\cos 30^{o}-G.{\frac {l}{2}}.\cos 30^{o}=0$

Uit de laatste vergelijking volgt: S = G/2
Invullen in de vorige vergelijkingen levert:

X_A = ${\sqrt {3}}G/4$

Y_A = 3G/4

3 samenlopende krachten

Wanneer er slechts 3 krachten in het spel zijn, eist de momentenvergelijking feitelijk dat de dragers van die 3 krachten door één punt gaan. Het gewicht en de spanning S snijden elkaar in het punt D. T.o.v. D hebben zij dus geen moment. Als men de kracht in A niet in componenten uittekent, maar als één kracht R_A, en men berekent het moment van alle krachten t.o.v. D, dan mag R_A geen moment hebben t.o.v. D opdat de som van alle momenten 0 zou zijn. Ook R_A moet dus door D passeren. Op basis van een klein beetje meetkunde kan men zien dat R_A dan onder een hoek van 30° met de verticale moet liggen. Men kan controleren dat de oplossing hieraan beantwoordt:

$\arctan {\frac {X_{A}}{Y_{A}}}=\arctan {\frac {{\sqrt {3}}G/4}{3G/4}}=\arctan {\frac {1}{\sqrt {3}}}=30^{o}$

De enige mogelijkheid dat de drie krachten niet door één punt gaan, is dat ze alle drie evenwijdig zijn. Men kan dan stellen dat het snijpunt op oneindig ligt.

Vrijheidsgraden en verbindingen

Een voorwerp waarvan de beweging aan geen enkele beperking onderworpen is, kan een willekeurige translatie en rotatie uitvoeren. Beide kunnen voorgesteld worden door een vector, die in onze reële wereld kan beschreven worden m.b.v. 3 basisvectoren. Men zegt daarom dat een vrij bewegend voorwerp 3 vrijheidsgraden van translatie heeft en 3 vrijheidsgraden van rotatie.

Meestal is elk voorwerp wel ergens in contact met een ander voorwerp. Dat contact belet dan sommige bewegingen, schakelt sommige vrijheidsgraden uit. Wanneer een voorwerp bv. op het horizontale oppervlak van een tafel moet blijven, dan heeft het nog 2 vrijheidsgraden van translatie. De vrijheid om in vertikale richting te bewegen is weggenomen. Het uitschakelen van die vrijheidsgraad vraagt een kracht vanwege de tafel op het voorwerp. Men noemt dit een verbindingskracht. Meestal worden deze verbindingskrachten ook gezien als reacties die optreden, doordat sommige actiekrachten het voorwerp willen laten bewegen in de richting van de verboden vrijheidsgraad (in dit geval is die actiekracht het gewicht). Rotaties kunnen belet worden door een moment.

Opdat men geen overbodige onbekenden zou invoeren, is het belangrijk dat men goed weet welke verbindings- of reactiekrachten er horen bij elk type verbinding.

voorbeeld van vrije contacten

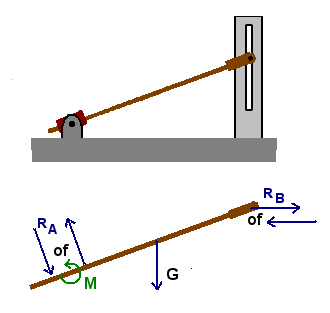
- vrij contact: een punt van het voorwerp wordt verplicht langs een vlak of lijn of in een gleuf te bewegen. De beweging loodrecht op dat vlak of lijn of gleuf is verboden. De verbindingskracht zal loodrecht op dat vlak of lijn of gleuf staan. De richting is dus bekend, alleen de grootte niet. Dit vormt dus 1 onbekende. (Voor de mof: zie verder bij inklemming)

Wanneer een voorwerp op een vlak rust, maar er eraf kan genomen worden, zal voor evenwicht nog nodig zijn dat de verbindingskracht naar het voorwerp wijst, d.i. een druk is tegen het voorwerp (en het voorwerp drukt dan ook tegen het vlak). Voor een pin in een gleuf zal men normaal onderstellen dat maar één van beide kanten van de gleuf in contact is met de pin en dat dus maar één van beide kanten een druk uitoefent op de pin.

Ook de roloplegging, zoals gebruikelijk in steunpunten van bruggen, is een vorm van vrij contact.

- scharnier. Men moet hier zien wat er door de constructie van het scharnier belet en wat toegelaten wordt. Een klassiek scharnier, zoals bij een deur, laat de rotatie toe rond de as van de scharnieren, maar belet elke translatie. Een rotatie toelaten betekent dat er geen moment kan overgebracht worden volgens die rotatieas.

• Voor een driedimensionaal probleem zal men 3 verbindingskrachten moeten invoeren en in principe ook 2 momenten. Wanneer een voorwerp met meerdere scharnieren bevestigd is, kan men onderstellen dat die momenten geleverd worden door de verbindingskrachten die op een zekere afstand van elkaar aangrijpen. Bij een bolscharnier is er natuurlijk alleen een reactiekracht met 3 componenten, omdat een rotatie in elke richting mogelijk blijft.
• Voor een tweedimensionaal probleem zal men alleen een verbindingskracht met 2 componenten moeten invoeren, zoals in het voorbeeld hierboven. Dit levert dus 2 onbekenden voor de vergelijkingen.

inklemming

- inklemming: een inklemming belet een translatie en rotatie van het verbindingspunt. Een inklemming onderstelt een zeker contactoppervlak met de omgeving, waardoor de krachten over een zekere afstand ingrijpen en zo een moment kunnen uitoefenen. Voor de eenvoud van de zaak wordt een inklemming meestal als een verbinding in één punt beschouwd en worden de momenten afzonderlijk ingevoerd. In drie dimensies zal men dus een reactiekracht en een moment met telkens 3 componenten moeten invoeren. In twee dimensies wordt dit een reactiekracht met 2 componenten en 1 moment. Die momentvector staat loodrecht op het vlak van de tekening en is dus moeilijk weer te geven. Hij wordt daarom meestal aangeduid door een gekromde pijl, die een rotatie suggereert in de richting waarin het moment een rotatie zou verwekken. Hierbij speelt de regel van de rechtse schroef. Als het pijltje een rotatie in wijzerzin voorstelt, dan is de momentvector van de toeschouwer weg gericht en omgekeerd.

Een staaf die door een mof glijdt, is een combinatie van een vrij contact met anderzijds het element van contact over een zeker oppervlak zoals bij de inklemming. Er zal dus een reactiekracht loodrecht op de mof en een moment moeten ingevoerd worden.

- touw: een touw kan alleen trekken in de richting van het touw (met uitzondering van sommige fakirstouwen). Men moet dus één onbekende kracht in de richting van het touw invoeren.

Ideale staaf

Wanneer men een staaf heeft die in slechts 2 punten verbonden is met een voorwerp en waarvan het eigen gewicht verwaarloosbaar is t.o.v. de krachten die optreden in die verbindingen, kan men door toepassen van de evenwichtsvergelijkingen gemakkelijk aantonen dat de verbindingskrachten in die contactpunten even groot maar tegengesteld moeten zijn (uit de eis som = 0) en dat ze in elkaars verlengde moeten liggen (om te voldoen aan som der momenten = 0). Ze schijnen als het ware een actie-reactiekoppel te vormen. Men zal normaal geen vergelijkingen opschrijven voor zo'n staaf, maar de kracht in die staaf berekenen uit het evenwicht van de voorwerpen waarmee ze in contact is. Bemerk echter wel dat het moet gaan om puntvormige contacten, d.i. vrij contact of scharnier, met de andere voorwerpen, niet om een inklemming. Voorbeelden van ideale staven vindt men in de voorbeelden van verschillende systemen hieronder.

Strikte evenwichtsvoorwaarden

Soms worden door de verbindingskrachten niet alle vrijheidsgraden uitgeschakeld. Denk bv. aan een deur die open staat. De scharnieren houden de deur op haar plaats, maar beletten geen rotatie rond de as van de scharnieren. Opdat de deur onbeweeglijk zou blijven, moet de som van de momenten van de uitwendige krachten t.o.v. die as 0 zijn. In de vergelijking die dat uitdrukt, zullen geen verbindingskrachten voorkomen maar alleen actieve krachten. Dit soort vergelijkingen, waarin alleen eisen gesteld worden aan de actieve krachten, noemt men ook wel de strikte of eigenlijke evenwichtsvoorwaarden.

Isostatisch, hyperstatisch en hypostatisch systeem

Als het aantal onbekenden (= componenten van onbekende verbindingskrachten of momenten) dat optreedt in een probleem, precies overeenkomt met het aantal vergelijkingen dat men kan opschrijven, heeft men een goed bepaald of isostatisch systeem. Deze benaming gaat echter uit van een wiskundige kijk op de zaak en betekent niet dat het evenwicht van het systeem dan echt mogelijk is. Het kan namelijk nog zo zijn dat de beschikbare verbindingskrachten op de verkeerde plaatsen aangrijpen of in de verkeerde richting werken. Zie voorbeeld 1 hieronder.

Wanneer een systeem minder onbekenden heeft dan vergelijkingen dan is het een onmogelijk of hypostatisch systeem. In de praktijk zijn vele van die systemen perfect in evenwicht, namelijk voorwerpen die alleen onder invloed zijn van het gewicht en die door verticale reacties in evenwicht gehouden worden (voorbeeld 2 hieronder). Zolang er geen zijdelingse krachten op die voorwerpen werken, is er ook geen zijdelingse reactie nodig. De projectie van alle krachten op een horizontale bevat gewoon niets en is dus een schijnbaar overbodige vergelijking.

Wanneer er meer onbekenden zijn dan vergelijkingen dan heeft men een onbepaald of hyperstatisch systeem. In feite is elke tafel of elke stoel met vier poten zo'n hyperstatisch systeem. Alleen een driepikkel is een isostatisch systeem. Men kan in zo'n geval, met de basisvergelijkingen van de statica, niet correct uitreken hoe de nodige reactiekracht zich zal verdelen over de aanwezige verbindingen. Er zit een onbepaaldheid in de verdeling van de krachten over de verbindingen. Men kan dikwijls een beroep doen op de elasticiteit van de contactpunten of van het systeem zelf om toch tot een verdeling van de krachten te komen. De elasticiteit van de ophanging van een auto zorgt er bijvoorbeeld. voor dat elk wiel in contact blijft met de grond, zelfs als er één wiel op de stoep staat en de drie andere op de rijweg. Als een tafel op een beetje losse grond staat, zal de ene poot wat dieper in de grond zakken dan de andere, tot er evenwicht is. Een balk op drie steunpunten die niet perfect collineair zijn, zal zich zo vervormen dat de balk toch op de drie steunpunten steunt (voor zover het hoogteverschil niet te groot is).

Voorbeelden

Voorbeelden

Voorbeeld 1: in theorie isostatisch, maar toch onmogelijk evenwicht. Als men het moment berekent t.o.v. het punt A, dan blijken alle verbindingskrachten door dit punt te gaan en dus geen moment te hebben t.o.v. dit punt. Het gewicht heeft echter wel een moment. Er is dus niet voldaan aan de momentenvergelijking en het voorwerp zal beginnen te draaien rond A. Zodra de staafverbinding schuin ligt, is er wel evenwicht mogelijk. Dan kunnen immers alle krachten door 1 punt gaan (voorbeeld 1b). Bemerk dat voor de schuine stand een langere staaf nodig is dan voor de horizontale stand van de staaf.

Isostatisch systeem

Voorbeeld 2: een onmogelijk systeem, want slechts 2 reactiekrachten, in feite perfect in evenwicht. Als er geen horizontale actiekracht is, is er ook geen horizontale reactie nodig.

Voorbeeld 3: een hyperstatisch systeem. In elk scharnier moeten 2 onbekende reacties ingevoerd worden. De projectie op een horizontale zegt dat er twee gelijke, maar tegengestelde horizontale krachten moeten zijn in de bevestigingspunten, maar zegt niets over de grootte ervan. Als de afstand tussen de bevestigingspunten perfect overeenkomt met de afstand tussen de gaten in de plaat, zijn die krachten gelijk aan 0. Als dat niet het geval is, introduceert men een spanning of druk in de plaat. De grootte hiervan heeft niets te maken met de formules van de statica.

Evenwicht van samengestelde voorwerpen

Samengestelde voorwerpen bestaan in drie categorieën:

• De samenstellende delen zijn onvervormbaar en ook het geheel is onvervormbaar.
• De samenstellende delen zijn onvervormbaar, maar het geheel is vervormbaar.
• Continu vervormbare systemen, zoals kettingen en kabels.

Het basisprincipe is dat voor evenwicht van het geheel elk onderdeel afzonderlijk in evenwicht moet zijn. Men moet dus de evenwichtsvoorwaarden, zoals die hoger gezien werden voor een onvervormbaar voorwerp, op elk van de onderdelen toepassen. Daarvoor zal men het voorwerp uit elkaar moeten halen, zodat duidelijk is over welk onderdeel men spreekt en wat de interacties zijn tussen die onderdelen.

krachten in een scharnier

Belangrijk is dat men bij het aanduiden van de krachten tussen de onderdelen erop let dat de actie-reactiewet gerespecteerd wordt. Als balk A een kracht uitoefent op balk B, dan zal balk B een gelijke, maar tegengesteld gerichte kracht uitoefenen op balk A. Eén van die krachten zal men een minteken meegeven, de andere zou in theorie een plusteken moeten krijgen, maar dat wordt normaal niet geschreven. Op die manier worden er dus geen 2 onbekende krachten ingevoerd, maar slechts één. Ook voor de projecties geldt dat elke projectie eenmaal als positief en eenmaal als negatief zal moeten voorkomen in de vergelijkingen. Als men de som maakt over het geheel, moeten de inwendige krachten immers tegen elkaar wegvallen.

Bemerk dat in de vectoriële notatie het plus- of minteken geen enkele aanduiding geeft over de richting van de betrokken vector. Het minteken zegt alleen dat er nog een even grote, maar tegengestelde kracht voorkomt in het systeem.

Samengesteld systeem, geheel onvervormbaar

man op ladder

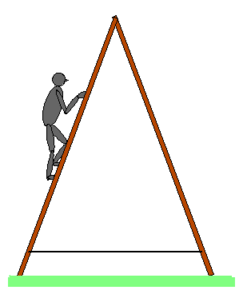
Als voorbeeld wordt een trapladder beschouwd (zie figuur). Als er tussen de onderste treden een staaf bevestigd is, dan is het geheel onvervormbaar. Deze ladder zou men ook op glad ijs kunnen plaatsen zonder risico dat men tegen het ijs slaat. Bij het uit elkaar halen werd voor de belasting door de man beroep gedaan op de stelling dat men een kracht mag verschuiven over zijn drager om zo tot een equivalente beschrijving te komen (zie het hoofdstuk over "gelijkwaardige vectorsystemen"). Op die manier kunnen we het gewicht van de man laten aangrijpen op de ladder op een afstand d van de grond.

man op ladder: onderdelen

Er worden geen vergelijkingen opgeschreven voor de ideale staaf tussen de treden. Men weet immers vooraf waartoe die zouden leiden (zie hierboven). Er worden tegengestelde krachten opgeschreven werkend op de linker- en rechterhelft van de ladder. In feite zijn die tegengestelde krachten het resultaat van driemaal even groot en tegengesteld:

• tussen linkerhelft van de ladder en de staaf op basis van de actie-reactiewet;
• tussen beide uiteinden van de staaf op basis van wat hierboven gezegd werd over krachten op een ideale staaf;
• tussen ideale staaf en rechterhelft van de ladder opnieuw volgens de actie-reactiewet.

Voor elk onderdeel moeten de evenwichtsvergelijkingen opgeschreven worden. Voor dit tweedimensionaal voorbeeld met 2 onderdelen levert dit 2x3 vergelijkingen = 6 vergelijkingen. Wanneer het systeem in zijn geheel onvervormbaar is, kan men ook op het geheel de evenwichtsvoorwaarden toepassen. Als krachten heeft men dan alleen de gewichten en de 2 verticale reacties in de steunpunten onderaan de ladder (zolang de ladder op een horizontaal vlak staat, anders moet er een zijdelingse reactie bijkomen in minstens een van de steunpunten). Als men het stelsel van vergelijkingen met de hand moet oplossen, biedt dit evenwicht van het geheel een mogelijkheid om het stelsel op te splitsen in een reeks kleinere stelsels, die met de hand veel gemakkelijker op te lossen zijn dan het grote stelsel. Hier zou men twee stelsel van drie vergelijkingen bekomen. De vergelijkingen voor het evenwicht van het geheel vormen een stelsel afhankelijke vergelijkingen. Ze kunnen rechtstreeks opgeschreven worden of gevonden worden door de projecties volgens elke as lid aan lid op te tellen. Na het invullen van de gevonden oplossingen in het grote stelsel heeft men dan een stelsel met drie onafhankelijke vergelijkingen minder. Hier kan men uit het evenwicht van het geheel de reactiekrachten in de steunpunten met de grond berekenen. Er blijven dan nog 3 onbekenden, X_AB, X_C ,Y_C, waarvoor nog juist 3 vergelijkingen nodig zijn. De vergelijkingen voor een der delen kunnen hiervoor dienen.

De vergelijkingen

Zij l de lengte van elk deel van de ladder, d_st de lengte van de grond tot het aangrijpingspunt van de staaf en d_m de lengte van de grond tot het aangrijpingspunt van het gewicht van de man, beide langs de ladder gemeten. Men veronderstelt dat het zwaartepunt van de ladder op halve hoogte ligt.

Voor de linkse helft:

• som van de krachten = 0:

$\sum X_{i}=-X_{C}+X_{AB}=0$

$\sum Y_{i}=Y_{A}+Y_{C}-G_{m}-G_{L}=0$

• som van de momenten t.o.v. A = 0 (positief gerekend in tegenwijzerzin):

$\sum M_{i}=-X_{AB}.d_{st}.\sin \alpha -G_{m}.d_{m}.\cos \alpha -G_{L}.(l/2).\cos \alpha +X_{C}.l.\sin \alpha +Y_{C}.l.\cos \alpha =0$

Dit vorm een stelsel van 3 vergelijkingen in 4 onbekenden. Dus nog niet oplosbaar.

Voor de rechtse helft:

• som van de krachten = 0:

$\sum X_{i}=-X_{AB}+X_{C}=0$

$\sum Y_{i}=Y_{B}-Y_{C}-G_{R}=0$

• som van de momenten t.o.v. B = 0 (positief gerekend in tegenwijzerzin):

$\sum M_{i}=X_{AB}.d_{st}.\sin \alpha +G_{R}.(l/2).\cos \alpha -X_{C}.l.\sin \alpha +Y_{C}.l.\cos \alpha =0$

Dit vorm ook een stelsel van 3 vergelijkingen in 4 onbekenden, ook niet afzonderlijk oplosbaar.

Alle vergelijkingen samen vormen echter een stelsel van 6 vergelijkingen in 5 onbekenden: Y_A, X_AB, X_C ,Y_C, Y_B. De ontbrekende onbekende is een zijdelingse reactie in een van de steunpunten, die hier niet nodig is.

Omdat het geheel onvervormbaar is, moeten de vergelijkingen voor het geheel afzonderlijk oplosbaar zijn:

• som van de krachten = 0:

$\sum X_{i}=0$: dit is een lege vergelijking.

$\sum Y_{i}=Y_{A}+Y_{B}-G_{m}-G_{L}-G_{R}=0$

• som van de momenten t.o.v. A = 0 (positief gerekend in tegenwwijzerzin):

$\sum M_{i}=-G_{m}.d_{m}.\cos \alpha -G_{L}.(l/2).\cos \alpha -G_{R}.(3l/2).\cos \alpha +Y_{B}.2l.\cos \alpha =0$

Dit vorm een stelsel van 2 vergelijkingen in 2 onbekenden: Y_A en Y_B. Deze laatste kan ogenblikkelijk uit de momentenvergelijking gehaald worden als:

$Y_{B}={\frac {2.G_{m}.d_{m}+G_{L}.l+G_{R}.3l}{4l}}$

Men kan de vergelijkingen voor het linkse en rechtse deel ook lid aan lid optellen om het evenwicht van het geheel te bekomen. Voor de momentenvergelijking is er echter een probleem omdat de momenten t.o.v. verschillende punten opgeschreven werden. Als men de momentenvergelijking voor het rechtse deel ook opschrijft t.o.v. A krijgt men:

$\sum M_{i}=X_{AB}.d_{st}.\sin \alpha -G_{R}.(3l/2).\cos \alpha -X_{C}.l.\sin \alpha -Y_{C}.l.\cos \alpha +Y_{B}.2l.\cos \alpha =0$

Als men dit optelt bij de momentenvergelijking voor het linkse deel, krijgt men ook de vorige momentenvergelijking.

Numeriek voorbeeld
Als men volgende waarden als gegeven invult:

• G_man = 800 N
• G_L = G_R = 100 N
• d_st = 0,3 m
• d_man = 1 m
• l = 2,5 m
• afstand tussen A en B = 2 m

dan krijgt men volgende numerieke oplossingen, in volgorde van de berekening:

• de hoek van de ladder met de horizontale: 66°25'
• Y_B = 260 N
• Y_A = 740 N
• Y_C = 160 N
• X_C = X_AB = 104,15 N

Samengesteld systeem, geheel vervormbaar

man op ladder

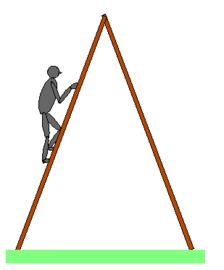
Neemt men bij vorig voorbeeld de staaf tussen de treden weg, dan bekomt men een systeem dat op zijn geheel vervormbaar is. Er zijn nu in de steunpunten zijdelingse reacties nodig om te beletten dat die zouden wegschuiven. Het grote verschil is nu dat men bij het toepassen van de evenwichtsvoorwaarden voor het geheel, niet meer een stelsel heeft dat op zichzelf oplosbaar is. In dit geval zit men met 3 vergelijkingen in 4 onbekenden: X_A, Y_A, X_B en Y_B (zie figuur hieronder). In vele gevallen kan men echter toch nog de momentenvergelijking voor het geheel opschrijven als een vergelijking in één onbekende, die ogenblikkelijk op te lossen is en zo een vertrekpunt kan vormen voor het handmatig oplossen van het stelsel. In dit geval kan men bv. de momentenvergelijking voor het geheel opschrijven t.o.v. het punt A of B. Dat zal een vergelijking leveren waarin resp. alleen Y_B of alleen Y_A voorkomt als onbekende. Als men zo bv. Y_B bepaald heeft, vormen de vergelijkingen voor het rechtse deel een stelsel van 3 vergelijkingen in 3 onbekenden dat op zich op te lossen is. Dan heeft men uiteindelijk nog 2 vergelijkingen nodig van het linkse deel om X_A en Y_A te bepalen. Als men alles in de computer kan steken, is dit geval niet moeilijker dan het vorige.

man op ladder: evenwicht van 't geheel

man op ladder: onderdelen

De vergelijkingen

Zij l opnieuw de lengte van elk deel van de ladder, d_m de lengte van de grond tot het aangrijpingspunt van het gewicht van de man langs de ladder gemeten. Men veronderstelt dat het zwaartepunt van de ladder op halve hoogte ligt.

Voor de linkse helft:

• som van de krachten = 0:

$\sum X_{i}=X_{A}-X_{C}=0$

$\sum Y_{i}=Y_{A}+Y_{C}-G_{m}-G_{L}=0$

• som van de momenten t.o.v. A = 0 (positief gerekend in tegenwijzerzin):

$\sum M_{i}=-G_{m}.d_{m}.\cos \alpha -G_{L}.(l/2).\cos \alpha +X_{C}.l.\sin \alpha +Y_{C}.l.\cos \alpha =0$

Voor de rechtse helft:

• som van de krachten = 0:

$\sum X_{i}=-X_{B}+X_{C}=0$

$\sum Y_{i}=Y_{B}-Y_{C}-G_{R}=0$

• som van de momenten t.o.v. B = 0 (positief gerekend in tegenwijzerzin):

$\sum M_{i}=G_{R}.(l/2).\cos \alpha -X_{C}.l.\sin \alpha +Y_{C}.l.\cos \alpha =0$

Dit vormt een stelsel van 6 vergelijkingen in 6 onbekenden: X_A, Y_A, X_C, Y_C, X_B, Y_B.

De momentenvergelijking t.o.v. A voor het geheel:

$\sum M_{i}=-G_{m}.d_{m}.\cos \alpha -G_{L}.(l/2).\cos \alpha -G_{R}.(3l/2).\cos \alpha +Y_{B}.2l.\cos \alpha =0$

Deze vergelijking is dezelfde als in het vorige geval, daar X_A en X_B geen moment hebben t.o.v. A. Ze bevat slechts 1 onbekende, namelijk Y_B, en deze kan dus onmiddellijk uitgerekend worden. De oplossing invoeren in de vergelijkingen voor het rechter deel leidt tot een stelsel van 3 vergelijkingen in 3 onbekenden dat afzonderlijk oplosbaar is. Daarna moeten nog 2 vergelijkingen van het linkse deel gebruikt worden voor de reacties in A. Men vindt dezelfde oplossingen voor de Y-componenten. Voor de X-componenten vindt men nu X_A = X_B = X_C = 91,66 N, iets minder dus dan de kracht in de staaf omdat de afstand tussen deze componenten groter is.

Meervoudige contacten

In de top van de ladder komen 2 delen samen. Bij het opsplitsen krijgt men actie en reactie tussen deze beide delen. Maar hoe moet men het geval behandelen van 3 of meer voorwerpen die in één punt met elkaar contact hebben? Die situatie noemt men een meervoudig contact.

meervoudig contact

In eerste instantie kan men telkens krachten tussen 2 voorwerpen tekenen. Dan kan men de actie-reactiewet toepassen. Vanuit A werkt op B de kracht F_AB. Op A heeft men dan de reactie F_BA. Om het aantal onbekenden niet nodeloos op te drijven, geeft men aan een reactiekracht normaal dezelfde naam als aan de actiekracht maar met een minteken:

${\vec {F}}_{BA}=-{\vec {F}}_{AB}$

Voor drie voorwerpen is dat nog juist overzichtelijk, voor meer wordt het moeilijk. Men wil liever één kracht op elk voorwerp veroorzaakt door alle andere voorwerpen, zoals in de derde schets. Die kracht wordt dan natuurlijk de som van de krachten uit de vorige beschrijving. Hiervoor geldt dan:

${\vec {F}}_{A}={\vec {F}}_{BA}+{\vec {F}}_{CA}=-{\vec {F}}_{AB}+{\vec {F}}_{CA}$

${\vec {F}}_{B}={\vec {F}}_{AB}+{\vec {F}}_{CB}=\ \ {\vec {F}}_{AB}-{\vec {F}}_{BC}$

${\vec {F}}_{C}={\vec {F}}_{AC}+{\vec {F}}_{BC}=-{\vec {F}}_{CA}+{\vec {F}}_{BC}$

Als men beide leden lid aan lid optelt, vindt men:

$\sum {\vec {F}}_{i}=0$

meervoudig contact met fictief knooppunt

In plaats van de actie-reactiewet komt nu de eis dat de som van als deze krachten nul is. Aan deze eis kan op een eenvoudige en veilige manier voldaan worden door het invoeren van een fictief knooppunt. In plaats van de voorwerpen met elkaar te laten interageren, laat men ze interageren met een zelf gecreëerd knooppunt, in dit geval het punt D. Tussen dit knooppunt en elk van de voorwerpen kan nu wel de actie-reactiewet toegepast worden. En voor een massaloos punt geldt in elk geval, versnelling of rust, dat de som van de krachten die erop werken moet nul zijn. Dit leidt op zeer eenvoudige manier tot de bijkomende vergelijking dat de som van alle krachten op D nul moet zijn. In die vergelijking komen dan in eerste instantie de tegengestelde krachten van de bovenstaande vergelijking, maar als men beide leden met -1 zou vermenigvuldigen, komt men op dezelfde vergelijking.

Bemerk dat het getekende systeem feitelijk hyperstatisch is. Er zijn 3 vlakke onderdelen, wat 3 x 3 vergelijkingen oplevert. Dan zijn er nog de 2 vergelijkingen voor het fictief knooppunt. Dat levert in totaal 11 vergelijkingen. Er zijn echter 6 vectoriële onbekenden, dus 12 scalaire onbekenden in het totaal. Men zou één uiteinde niet via een scharnier maar via een gleuf moeten bevestigen. Dan zou er voor die verbinding maar één onbekende zijn (de kracht loodrecht op de gleuf) i.p.v. twee zoals bij een scharnier en zou men 11 onbekenden hebben voor 11 vergelijkingen.

Vakwerken

Definitie

Voorbeeld van vakwerk

Bij het bouwen van bruggen, bij het ontwerpen van een dak boven een fabriekshal of spoorwegstation wenst men dikwijls een zo groot mogelijke stijfheid en draagkracht te bekomen met een minimum aan materiaal. Hiervoor wordt dan dikwijls beroep gedaan op vakwerken, constructies die bestaan uit relatief lichte staven of balken, soms aangevuld met kabels. Een torenkraan is ook een mooi voorbeeld van een constructie waarbij maximale stijfheid bereikt wordt met een minimum aan materiaal, zowel voor het verticale deel, de toren, als voor de arm. Bij deze (inleidende) bespreking zullen echter alleen vlakke vakwerken besproken worden. In het Engels spreekt men van "trusses".

Bij het ontwerp van een vakwerk gaat men ervan uit dat

• het eigen gewicht van de staven verwaarloosbaar is in vergelijking met de krachten die erin optreden;
• de verbindingen in eerste instantie als scharnierend beschouwd worden. Dit betekent dat de stijfheid moet komen van de juiste plaatsing van de staven, niet van de stijfheid in de verbindingen;
• dat de belasting(en) aangrijpen in de knooppunten (en dus niet ergens op de staven).

Onder deze onderstellingen moeten de krachten in de staven volgens de staven liggen, zoals hoger vermeld onder ideale staaf. Men zal dus geen vergelijkingen opschrijven voor de staven, maar alleen voor de knooppunten. Op beide einden van elke staaf werken gelijke, maar tegengestelde krachten werken. Deze krachten kunnen de staaf samendrukken of uitrekken. In het eerste geval zegt men dat de staaf onder druk staat, in het tweede dat ze onder trek staat. Daar het woord "spanning" verwijst naar trek, wordt conventioneel een trekkracht in een staaf aangeduid met een plusteken en druk met een minteken. Deze aanduidingen van het resultaat van de berekeningen heeft echter niets te maken met de tekens die in de vergelijkingen kunnen voorkomen. Soms werden de stukken die op druk belast worden, in hout uitgevoerd, soms werden stukken die op trek belast worden, vervangen door kabels. Voor stukken die op druk belast worden, moet men opletten voor het "knikken" van het materiaal. Het risico hiervoor is kleiner bij een houten balk van voldoende dikte dan bij metalen profielen. Om een idee te krijgen of een staaf op druk of trek belast wordt, kan men zich inbeelden dat men de staaf wegneemt en dan de vraag stellen of de knooppunten waartussen deze staaf bevestigd was, naar elkaar toe zouden komen (druk) of uit elkaar zouden gaan (trek). Het is op die manier vrij duidelijk dat bv. de staaf BC op druk belast is en de staaf AE op trek.

Vakwerk met alle krachten

Voor elke knooppunt moet gelden dat de som van de krachten 0 is. De krachten op de knooppunten zijn de reacties van de krachten op de staven. Wanneer een kracht op een staaf drukt, zal de reactie ook op het knooppunt drukken. Trek of druk op de staaf blijven dus ook trek of druk op het knooppunt. Een voorbeeld van een volledige opsplitsing van het hoger gegeven vakwerk vindt men in de figuur hiernaast. De zin van de krachten is niet overal correct. Dat zal ook blijken in de berekening hieronder. Bemerk dat ook de krachten die een staaf op de knooppunten uitoefent, gelijk maar tegengesteld zijn. Opdat het systeem niet hyperstatisch zou zijn, wordt het meestal aan de omgeving bevestigd door een scharnier (hier in A) een een roloplegging (hier in D). Dit levert 2 uitwendige krachtcomponenten in A en één verticale kracht in D.

Om de krachten in alle staven te vinden, zal men moeten vertrekken van een knooppunt met maar 2 onbekende krachten, aangezien er slecht 2 projecties kunnen opgeschreven worden. Meestal bestaat zulk een knooppunt niet. Daar het vakwerk in zijn geheel echter onvervormbaar is, kan men ook het evenwicht voor het geheel afzonderlijk opschrijven. Dit levert drie vergelijkingen waaruit de drie uitwendige krachten kunnen worden berekend. Eens dat gebeurd heeft men zowel in A als in B een knooppunt met maar 2 onbekenden. Vertrekkend van A kan men bv. de krachten in de staaf AB en AE uitrekenen. Dan blijven er in B ook maar 2 onbekenden meer, waarna er zowel in C als E maar 2 onbekenden overblijven. Er blijven echter maar 3 onbekende staafkrachten meer te berekenen, zodat men van de 4 vergelijkingen en maar 3 zal moeten gebruiken. De vergelijkingen van het knooppunt D blijkt men niet meer nodig te hebben. Dat is niet verwonderlijk. De vergelijkingen van het evenwicht voor het geheel kunnen afgeleid worden uit de vergelijkingen voor de knooppunten. Als k het aantal knooppunten is, dan blijven er in het stelsel maar 2k-3 onafhankelijke vergelijkingen over. Dit levert een eerste manier om het aantal staven in een vakwerk te bepalen. Aangezien er maar 2k-3 vergelijkingen overblijven voor het bepalen van de krachten in de staven, mogen er ook maar 2k-3 staven in een vakwerk zijn.

Bepalen van aantal staven

Er is nog een andere manier om aan dat aantal te geraken. Het kleinste vakwerk bestaat natuurlijk uit een driehoek. Dat heeft 3 staven en 3 knooppunten. Als men iets wil toevoegen dan is het minimaal 1 knooppunt en 2 staven. Dan heeft men 4 knooppunten en 5 staven. Elke toevoeging van een knooppunt betekent ook 2 staven meer. De formule wordt dus:

aantal staven = (2 x aantal knooppunten) - 3

Bij sommige constructies worden staven gebruikt waarin geen kracht schijnt op te treden. Dit is bijvoorbeeld. het geval in knooppunten waar 3 staven samenkomen, waar geen uitwendige belasting is en waar 2 van de 3 staven perfect in elkaars verlengde liggen. Men moet er echter rekening mee houden dat er altijd een lichte vervorming optreedt onder belasting. Die schijnbaar overbodige verbindingen kunnen dan wel een rol gaan spelen. Ook kunnen ze een rol spelen als er wel een belasting komt op het knooppunt. Een belangrijke ontwikkelaar van vakwerken voor daken van fabriekshallen en stations was de Fransman Polonceau. Een van zijn eerste vakwerken was een overspanning voor het dak van een station in Parijs in 1837. Zijn naam staat ook vermeld op de Eiffeltoren. Zijn naam is ook verbonden aan het vakwerk in de figuur hieronder.

Er is een grote verscheidenheid aan vakwerken mogelijk. De driedimensionele vakwerken, zoals bij een torenkraan, kwamen pas na de 2de wereldoorlog volop in gebruik.

Ontwerpen van Polonceau

Berekening

Als voorbeeld wordt de berekening van alle krachten van bovenstaand voorbeeld uitgevoerd. Er wordt ondersteld dat alle driehoeken gelijkzijdig zijn (dan zijn alle hoeken 60°) met een zijde van 2 m en dat de kracht F = 500 kg. De projecties van de krachten krijgen een teken volgens de zin die in de figuur hierboven gegeven is. De resultaten moeten dan positieve getallen zijn. Een negatieve uitkomst duidt op een verkeerd ingeschatte zin van de kracht.

Evenwicht van het geheel:
$\sum X_{i}=X_{A}=0$
$\sum Y_{i}=Y_{A}+Y_{D}-500=0$
Moment t.o.v. A:
$-2*500+4*Y_{D}=0$
Hieruit volgt: Y_D = 250 kg
Uit vorige vergelijking volgt dan: Y_A = 250 kg

Voor knooppunt A:
$\sum X_{i}=S_{AE}+S_{AB}\cos 60+X_{A}=0$
$\sum Y_{i}=S_{AB}\sin 60+Y_{A}=0$
Hieruit volgt S_AB = - Y_A/sin 60° = -288,7 kg . Het minteken van het resultaat betekent dat de zin van de kracht in de staaf AB verkeerd ingeschat werd. Het moet druk zijn i.p.v. trek.
S_AE = - S_ABcos 60° = -(-288,7)*0.5 = 144,3 kg (trek)

Knooppunt B, met S_AB als druk:
$\sum X_{i}=-S_{BC}+S_{AB}\cos 60-S_{BE}\cos 60=0$
$\sum Y_{i}=S_{AB}\sin 60+S_{BE}\sin 60=0$
Bij de laatste vergelijking is duidelijk iets fout: de som van 2 positieve getallen kan nooit 0 worden. De zin van een kracht is dus verkeerd. S_BE moet een trek zijn. Men krijgt dan als vergelijkingen:
$\sum X_{i}=-S_{BC}+S_{AB}\cos 60+S_{BE}\cos 60=0$
$\sum Y_{i}=S_{AB}\sin 60-S_{BE}\sin 60=0$
Uit de laatste vegelijking volgt dadelijk: S_BE = S_AB = 288,7 kg (trek)
Uit de vorige vergelijking volgt dan: S_BC = 2*S_ABcos 60° = 288,7 kg (druk)

Knooppunt C:
$\sum X_{i}=S_{BC}+S_{CE}\cos 60-S_{CD}\cos 60=0$
$\sum Y_{i}=S_{CE}\sin 60+S_{CD}\sin 60=0$
Hier kan weer dezelfde opmerking gemaakt worden. Het is duidelijk dat S_CE op trek belast wordt. Men vindt:
S_CE = S_BC/(2*cos 60°) = 288,7 kg (trek)
S_CD = S_CE = 288,7 kg (druk)

Om de kracht in staaf DE te bepalen, wordt beroep gedaan op knooppunt D:
$\sum X_{i}=S_{CD}\cos 60-S_{DE}=0$
Hieruit volgt: S_DE = 144,3 kg (trek).

Vakwerk met krachten

Continu vervormbare media

Bij een ketting heeft men een vervormbaar systeem dat opgebouwd is uit onvervormbare delen, maar deze delen zijn klein t.o.v. het geheel. Bij een touw of een kabel kan men zelfs geen delen meer onderscheiden. Men heeft dan een continu vervormbaar medium. Hier zal het evenwicht van een kabel en de doorbuiging van een balk besproken worden als eenvoudige voorbeelden van evenwicht in continu vervormbare media. Voor een grondiger bespreking moet men zich tot de Sterkteleer of de Continuum Mechanica wenden.

Kettingen en kabels

Men beschouwt een kabel die opgehangen is tussen de punten A en B. Het totale gewicht van de kabel is G_k. Dit gewicht grijpt aan in het massacentrum van de kabel, voor een homogene dus in het midden. De hele kabel moet natuurlijk in evenwicht zijn:

Doorhangende kabel

$-F_{Ax}+F_{Bx}=0$

$F_{Ay}+F_{By}=G_{k}$

Men zou ook nog de momentenvergelijking kunnen opschrijven. Wanneer men een willekeurig punt C op de kabel beschouwt en veronderstelt dat men de kabel daar doorsnijdt, dan zal men op elk deel van de kabel een kracht T moeten uitoefenen om de beide einden bij elkaar te houden. Dit noemt men de spanning in de kabel. Wat hierboven gezegd is over de projecties op de x-as voor het punt B, geldt dan ook voor spanningen in C. M.a.w T_x = F_A,x = constant (I).

Als men een klein stukje van de kabel met lengte Δx beschouwt in het punt met coördinaten (x,y), dan kan men zeggen dat er links een kracht T(x) op werkt en rechts een kracht T(x+Δx). Volgens wat hierboven gezegd werd, moet de x-component van beide gelijk zijn en gelijk aan F_A,x. Het gewicht van het stukje kabel kan men schrijven in functie van g_l, het gewicht per meter in de x-richting, als ΔG = g_l.Δx . Men krijgt dan in de y-richting:

$-T_{y}(x)+T_{y}(x+\Delta x)=g_{l}(x)\Delta x$

Stukje kabel

Deelt men beide leden door Δx en laat men Δx naar 0 gaan, dan wordt dit:

${\frac {d}{dx}}T_{y}(x)=g_{l}(x)$

In de limiet moeten beide spanningen de richting hebben van de raaklijn aan de kabel:

${\frac {dy}{dx}}={\frac {T_{y}(x)}{T_{x}}}$      (II)

Men differentieert dit nogmaals, met T_x = constant, en substitueert de uitdrukking die hierboven gevonden werd voor de afgeleide van T_y:

${\frac {d^{2}y}{dx^{2}}}={\frac {g_{l}(x)}{T_{x}}}$      (III)

Met deze vergelijkingen kan men nu een paar concrete gevallen bekijken.

Hangbrug

hangbrug

Men veronderstelt dat het eigen gewicht van de kabel en van de verticale verbindingen klein is in vergelijking met het gewicht van het brugdek. Voor het brugdek mag men onderstellen dat het gewicht per meter in horizontale richting constant is. Dan krijgt men als basisvergelijking:

${\frac {d^{2}y}{dx^{2}}}={\frac {g_{l}}{T_{x}}}$

waarbij het rechterlid een constante is. Na dubbele integratie krijgt men dus

$y(x)={\frac {g_{l}}{T_{x}}}{\frac {x^{2}}{2}}+C_{1}x+C_{2}$

De vorm van de kabel is in dit geval een parabool. De vergelijking bevat 3 constanten. Hiervoor heeft men 3 randvoorwaarde die moeten voldaan zijn:
- de kabel moet door de punten A en B passeren: y(x_A)= h_A en y(x_B)= h_B.
- De spanning Tx hangt vooral af van de lengte van de kabel t.o.v. de afstand AB:

$L=\int _{A}^{B}{\sqrt {dx^{2}+dy^{2}}}=\int _{A}^{B}{\sqrt {1+\left({\frac {dy}{dx}}\right)^{2}}}dx=\int _{A}^{B}{\sqrt {1+\left(C_{2}+{\frac {g_{l}}{T_{x}}}x\right)^{2}}}$

Deze integraal kan herleid worden tot de standaard vorm:

$\int {\sqrt {a^{2}+x^{2}}}dx={\frac {1}{2}}\left[x{\sqrt {a^{2}+x^{2}}}+a^{2}\log \left(x+{\sqrt {a^{2}+x^{2}}}\right)\right]$

- Ofwel gebruikt men de positie van het laagste punt, y'=0, als die bekend is.

De spanning in A en B tenslotte kan nu ook opgeschreven worden:

$F_{A}={\sqrt {F_{A,x}^{2}=F_{B,x}^{2}}}=T_{x}{\sqrt {1+\left({\frac {dy}{dx}}(x_{A})\right)^{2}}}$

en analoog voor de F_B.

Doorhangende kabel

In dit geval is het gewicht per meter constant, niet het gewicht per horizontale afstand. Een stukje met horizontale lengte Δx heeft een lengte Δl. Men krijgt dan voor het gewicht ervan:

$g_{l}(x)\Delta x=g\mu {\frac {\Delta l}{\Delta x}}\Delta x$

met μ de massa per meter. In de limiet, voor δx gaande naar 0, wordt dit:

$g_{l}(x)=g\mu {\frac {dl}{dx}}=g\mu {\frac {\sqrt {dx^{2}+dy^{2}}}{dx}}=g\mu {\sqrt {1+\left({\frac {dy}{dx}}\right)^{2}}}$

Invoeren in de vergelijking voor de 2e afgeleide levert:

${\frac {d^{2}y}{dx^{2}}}={\frac {g\mu }{T_{x}}}{\sqrt {1+\left({\frac {dy}{dx}}\right)^{2}}}$

De oplossing hiervan is een cosh (hyperbolische cosinus) of kettinglijn:

$y(x)={\frac {T_{x}}{g\mu }}\left[\cosh \left({\frac {g\mu }{T_{x}}}x+C_{1}\right)+C_{2}\right]$

Er zijn weer 3 constanten, die men uit de randvoorwaarden moet halen, zoals hierboven. Voor de hyperbolische functies gelden volgende betrekkingen:

$1+\cosh ^{2}=\sinh ^{2},\quad {\frac {d}{dx}}\sinh(x)=\cosh(x),\quad {\frac {d}{dx}}\cosh(x)=\sinh(x),\quad \cosh(0)=1,\quad \sinh(0)=0$

De uitdrukking voor de lengte van de kabel blijkt nu echter eenvoudiger:

${\begin{matrix}L=\int _{A}^{B}{\sqrt {1+({\frac {dy}{dx}})^{2}}}dx=\int _{A}^{B}{\sqrt {1+(\sinh({\frac {g\mu }{T_{x}}}x+C_{1}))^{2}}}=\int _{A}^{B}\cosh({\frac {g\mu }{T_{x}}}x+C_{1})\\={\frac {T_{x}}{g\mu }}\left[\sinh({\frac {g\mu }{T_{x}}}x_{A}+C_{1})-\sinh \left({\frac {g\mu }{T_{x}}}x_{B}+C_{1}\right)\right]\end{matrix}}$

De constanten moeten meestal via iteratie bepaald worden.

Er treden vereenvoudigingen op indien de ophanging symmetrisch is en men de x-as door AB neemt met de oorsprong in het midden van AB. De vorm van de kromme is dan:

$y(x)={\frac {T_{x}}{g\mu }}\left[\cosh \left({\frac {g\mu }{T_{x}}}x\right)-\cosh \left({\frac {g\mu }{T_{x}}}{\frac {AB}{2}}\right)\right]$

En de lengte van de kabel:

$L={\frac {T_{x}}{g\mu }}2\sinh \left({\frac {g\mu }{T_{x}}}{\frac {AB}{2}}\right)$

De afstand van de lijn tussen A en B en het diepste punt van de kabel is dan:

$h_{m}=|y(0)|={\frac {T_{x}}{g\mu }}\left[\cosh \left({\frac {g\mu }{T_{x}}}{\frac {AB}{2}}\right)-1\right]$

Galileo dacht dat de vorm van een doorhangende ketting of kabel een parabool was. Bernouilli was de eerste om de correcte vorm te vinden. Het verschil is echter klein. Men kan de parabool als een 1e-ordebenadering beschouwen. De kettinglijn is iets smaller dan de parabool. Andere afleidingen (bv. Katenoide in de Duitse Wikipedia) tonen aan dat de vorm onafhankelijk is van μ en g.

Deze vergelijkingen worden dikwijls afgeleid door een stukje te beschouwen met lengt s en vertrekkend naar rechts vanaf het onderste punt. Men vindt dat dat de T_y moet gelijk zijn aan het gewicht van dit stukje. Dit afleiden naar x levert een uitdrukking als hierboven

${\frac {T_{y}(s)}{dx}}=g\mu {\frac {ds}{dx}}=g\mu {\frac {\sqrt {dx^{2}+dy^{2}}}{dx}}=g\mu {\sqrt {1+\left({\frac {dy}{dx}}\right)^{2}}}$

Doorbuiging van een balk

Euler-Bernoulli vergelijking

Een tweede voorbeeld van een vervorming van een continu medium wordt de doorbuiging van een balk beschouwd. Voor de eenvoud van deze introductie wordt er ondersteld dat de balk een rechthoekige doornsnede heeft en dat die doorsnede over de ganse lengte dezelfde is. Verder wordt ondersteld dat de vervormingen klein zijn, zodat de doorsnedes steeds loodrecht blijven op de zijden van de balk. Men beschouwt de doorbuiging onder een gelijkmatig verdeelde last, in eerste instantie het eigen gewicht van de balk. Ook wordt ondersteld dat de einden van de balk niet ingeklemd zijn.

doorbuigende balk

Om de vorm van de balk te kunnen afleiden moet eerst de wet van Hooke in herinnering gebracht worden. Deze stelt dat de vervorming van een lichaam binnen een groot gebied (het elasticiteitsgebied) evenredig is met kracht. Als men een te grote kracht aanlegt, komt men in het plastische gebied, waar de evenredigheid niet meer opgaat. Voor een veer is de evenredigheidsfactor de stijfheid k, voor een kabel of ander stuk materiaal is het de elasticiteitsmodulus E, ook wel modulus van Young genoemd. Men kan de wet dan schrijven in de vorm:

$\sigma =E\epsilon$

met σ de spanning (kracht per oppervlak), ε de relatieve uitrekking (Δ L/L).

De eenheid van E is N/m² of Pa (Pascal). In de praktijk levert dit veel te grote waarden en gebruikt men de N/mm² of Mpa (Megapascal). Staal heeft een elasticiteitsmodulus van rond 2.10⁵ MPa.

buiging en kromtestraal

Wanneer een balk doorbuigt, zoals in de figuur, wordt de onderzijde uitgerekt en de bovenzijde samengedrukt. Tussen beide in ligt een neutraal vlak waarin geen vervorming optreedt. Als de doorsnede symmetrisch is, zal dit neutraal vlak in het midden liggen. Wanneer men een doorsnede loodrecht op de lengterichting van de balk bekijkt, zullen deze vervormingen toenemen met de afstand van het neutrale vlak. Volgens de wet van Hooke ontstaan er dan spanningen, die een moment M_z opbouwen t.o.v. een as in het neutrale vlak en loodrecht op de zijden van de balk.

Om de differentiaalvergelijking op te stellen beschouwt men een zeer klein stukje van de gebogen balk met dikte Δx. Men kan de vorm dan benaderen door de osculerende cirkel met straal ρ. De neutrale lijn heeft dan een lengte R.dθ, een punt erboven of eronder een lengte (R+y)dθ. De totale vervorming is dus y.dθ

De relatieve vervorming is:

$\epsilon ={\frac {y.d\theta }{\rho .d\theta }}={\frac {y}{\rho }}$

Spanningen in de doorsnede

Onderstelt men nu dat er geen resulterende horizontale spanning is in de balk, dan moet de som van de spanningen door de vervormingen 0 zijn. Dit veronderstelt dat het neutrale vlak door het zwaartepunt van de doorsnede passeert. Het moment van die spanningen is echter niet 0! Het wordt berekend door het moment van de spanningen te integreren over de oppervlakte S van de doorsnede. Hiervoor wordt elke spanning vermenigvuldigd met de afstand tot de z-as:

$M_{z}=\int _{S}\sigma _{x}.y.dS=\int _{S}E{\frac {y}{\rho }}.y.dS={\frac {E}{\rho }}\int _{S}y^{2}dS$

De integraal noemt men het oppervlaktetraagheidsmoment I. Zoals het traagheidsmoment, dat bij de rotatie gebruikt werd, wordt er vermenigvuldigd met het kwadraat van een afstand, maar hier wordt over het oppervlak geïntegreerd i.p.v. over het volume. Men noemt die y² ook de gewichtsfactor of kortweg het gewicht. Dus:

$I_{z}=\int _{S}y^{2}dS$

Voor een rechthoekige doorsnede met hoogte h en breedte b levert dit I = h³b/12 = h²S/12 , met S het totale oppervlak van de doorsnede. Men ziet dat de formules analoog zijn aan die voor het massatraagheidsmoment bij de rotatie, alleen komt er nu S in voor i.p.v. de totale massa m. Men kan hiermede de uitdrukking voor het moment herwerken tot:

${\frac {1}{\rho (x)}}={\frac {M_{z}(x)}{EI}}$

De kromtestraal ρ wordt gedefinieerd als:

${\frac {1}{\rho }}={\frac {y''}{\sqrt {1+y'^{2}}}}$

Het gaat hier over doorbuigingen die met het blote oog nauwelijks merkbaar zijn. y' is dus klein en de uitdrukking herleidt zich tot 1/ρ = y''. Indien deze onderstelling niet opgaat, zal men de correcte formule moeten gebruiken. Hiermede kan men de basisvergelijking voor de buiging van een balk opstellen:

${\frac {d^{2}y(x)}{dx^{2}}}={\frac {M_{z}(x)}{EI_{z}}}$

Deze formule wordt de Euler-Bernoulli vergelijking genoemd (zie in de Engelse Wikipedia onder "Euler-Bernoulli beam equation").. Ze geeft de vervorming van een klein stukje balk als er op beide zijden een moment M, maar met tegengestelde zin, uitgeoefend wordt.

Maar wat is het moment dat in deze formule voorkomt? Het kleine stukje dikte Δx, waarvoor de formule geldt, kan zich op elke punt van de balk bevinden. Dan is het moment links het moment dat door het linkse deel van de balk, tot op die plaats, op het stukje uitgeoefend wordt en analoog voor rechts. Als geen ander moment op het stukje uitgeoefend wordt, dan moeten die momenten even groot zijn, maar met tegengestelde zin. Als de dikte Δx van dit stukje naar 0 gaat wordt dit herleid tot een vlak. Het moment in de formule is dus het moment dat het ene stuk van de balk op het andere uitoefent ter hoogte van dit vlak. Om een duidelijk zicht te hebben op die krachten en momenten, moet men een snede aanbrengen op die plaats. Men beeldt zich in dat de balk op die plaats doorgesneden wordt loodrecht op de x-as. Vervolgens zoekt men welke krachten en momenten men op beide vrijgekomen doorsneden moet uitoefenen, opdat beide stukken op hun plaats zouden blijven. Op elk stuk kan een kracht en een moment aangrijpen, elk met 3 componenten. Volgens de 3e wet van Newton moet wat op het linkse deel aangrijpt even groot zijn als wat op het rechtse aangrijpt, maar met tegengestelde zin. Als er alleen verticale uitwendige krachten op de balk werken, zal er in de snede ook alleen een verticale kracht nodig zijn op basis van de formules voor het evenwicht van elk stuk. Als er geen uitwendig moment volgens de x-as (torsie volgens de langsrichting) of volgens de y-as (torsie volgens de verticale) uitgeoefend wordt, zal er ook in de snede geen moment nodig zijn volgens die assen. Hier is vooral het moment volgens de z-as belangrijk. Als men een snede op positie x beschouwt, kan men de momenten die door het stuk rechts uitgeoefend worden op het stuk links, startend in x=0, op 2 manieren berekenen: door het evenwicht der momenten te beschouwen t.o.v. de snede of door de momenten uit te rekenen uitgeoefend door het rechtse deel op het linkse. Voor de eenvoud van de zaak volgt men voor dit eerste voorbeeld de eerste methode. Men moet dan rekenen met

buiging van een balk

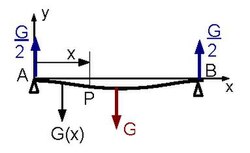
- een moment van de kracht in het steunpunt A. De kracht in elk steunpunt moet de helft zijn van het gewicht. F_A = G/2 = gμL/2 , met g de gravitatieversnelling en μ de massa per meter. Het tegengestelde moment is dan x.F_A = gμLx/2
- het moment van het stuk balk links van de snede. Dit stuk heeft lengte x en het gewicht ervan grijpt aan in het midden ervan. Het tegengestelde moment is -(gμx)(x/2)
Het totale moment in x is dus: (gμ/2)(Lx- x²). Invullen in de vergelijking:

$y''(x)={\frac {g\mu }{2EI}}(Lx-x^{2})$

Na integreren krijgt men:

$y'(x)={\frac {g\mu }{2EI}}\left({\frac {Lx^{2}}{2}}-{\frac {x^{3}}{3}}\right)+C_{1}$

Men kan de waarde van C₁ nu al bepalen uit het feit dat de raaklijn horizontaal moet zijn in het midden van de balk, dus uit y'(L/2) = 0. Na invullen wordt y'(x):

$y'={\frac {g\mu }{2EI}}\left({\frac {Lx^{2}}{2}}-{\frac {x^{3}}{3}}\right)-{\frac {g\mu \,L^{3}}{24EI}}={\frac {g\mu }{2EI}}\left({\frac {Lx^{2}}{2}}-{\frac {x^{3}}{3}}-{\frac {L^{3}}{12}}\right)$

Nogmaals integreren levert:

$y(x)={\frac {g\mu }{2EI}}\left({\frac {Lx^{3}}{6}}-{\frac {x^{4}}{12}}-{\frac {L^{3}x}{12}}\right)+C_{2}$

Uit het feit dat y(0) = 0 is, volgt dat C₂ = 0. Men krijgt:

$y(x)={\frac {g\mu }{24EI}}(2Lx^{3}-x^{4}-L^{3}x)$

Men kan controleren dat ook y(L) =0 is.

De maximale uitwijking is in het midden:

$|y(L/2)|={\frac {5g\mu }{24.16.EI}}L^{4}$

Dat betekent dat de doorbuiging, voor een zelfde type balk, toeneemt met de 4de macht van de lengte.

Ingeklemde balk

Als tweede voorbeeld wordt een balk beschouwd die maar aan een zijde vastgemaakt is. Voor evenwicht is dan vereist dat daar een inklemming is die zowel een kracht F_A als een moment M_A kan uitoefenen op de balk. Omwille van dat bijkomende moment is het hier eenvoudiger om het moment in de snede te berekenen op basis van de kracht die op het rechter stuk werkt. Dat is immers alleen het gewicht van dat stuk, in het midden ervan.

ingeklemde balk met vrij uiteinde

$\displaystyle M_{z}=-\mu g(L-x)(L-x)/2=(\mu g/2)(L-x)^{2}$

$y''(x)={\frac {-g\mu }{2EI}}(L-x)^{2}$

Na eerste integratie:

$y'(x)={\frac {+g\mu }{6EI}}(L-x)^{3}+C_{1}$

Uit y'(0) = 0 kan men C₁ bepalen. Invullen en nogmaals integreren levert:

$y(x)={\frac {g\mu }{6EI}}\left[{\frac {-(L-x)^{4}}{4}}-L^{3}x\right]+C_{2}$

Uit y(0) = 0 volgt de waarde voor C₂. Invullen levert:

$y(x)={\frac {-g\mu }{24EI}}(x^{4}-4Lx^{3}+2L^{2}x^{2})$

De doorbuiging of punt op het einde is:

$|y(L)|={\frac {g\mu }{8EI}}L^{4}$

Als men met evenwicht van de momenten op het stuk links zou werken, moet men vertrekken van:

$y''(x)={\frac {1}{EI}}\left({\frac {-GL}{2}}+F_{A}x-{\frac {\mu gx^{2}}{2}}\right)={\frac {\mu g}{2EI}}(-L^{2}+2Lx-x^{2})$

Voor het momentenevenwicht van het stukje AP is de eerste term hierin het tegengestelde van het inklemmingsmoment M_A, de tweede het tegengestelde van het moment van de kracht F_A en de derde het tegengestelde van het moment van het gewicht van het stukje AP. Men kan gemakkelijk controleren dat dit tot dezelfde oplossing leidt. En, alhoewel het opstellen van de eerste vergelijking wat ingewikkelder is, is de rest van de berekening eenvoudiger.

Als men de doorsnede van de balk in elke richting vergroot met een factor k, stijgt I met k⁴, maar μ met k². Netto daalt de breuk μ/I en dus de doorbuiging met k². Als men 2 planken op elkaar legt, zal de draagkracht verdubbelen. Als men die 2 planken aan elkaar kan lijmen tot één balk van dubbele doorsnede, wordt de draagkracht 4 maal groter.

Uit de berekening van het oppervlaktetraagheidsmoment blijkt dat de punten het verst van het neutrale vlak het meest bijdragen tot de draagkracht van de balk. Daarom worden stalen balken dikwijls in de vorm van een hoofdletter $\mathrm {I}$ gemaakt of gebruikt men kokervormige balken.

Bij belastingen in sommige punten zal men meerdere differentiaalvergelijkingen moeten opstellen omdat het moment in de snede rekening moet houden met die belasting als men de puntbelasting gepasseerd is.

Referenties

De meeste werken over mechanica besteden weinig of geen aandacht aan de statica. Wanneer dat wel het geval is, is het meestal in een afzonderlijk volume. In de bibliografie kan men dit zien bij de boeken van [meriam], [beer] en [smith].