Klassieke Mechanica/Kinematica-3
Kinematica-3: Aanvullingen
[bewerken]Ogenblikkelijk rotatiecentrum
[bewerken]Wanneer een wiel rolt zonder slippen, dan heeft het contactpunt met de grond dezelfde snelheid als de grond. De snelheid van de grond is 0 en het contactpunt staat dus ook stil. Het is alsof het wiel op elk ogenblik roteert rond het punt dat op dat ogenblik het contactpunt met de grond is. Daarom noemt men dat punt het ogenblikkelijk rotatiecentrum (voornamelijk in België) of momentane pool (voornamelijk in Nederland).
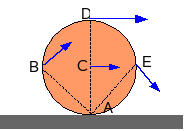
Als het wiel in de figuur hiernaast rolt met een hoeksnelheid ω, dan geldt:
- vA = 0
- vC = r.ω
- vB = vE = √2.r.ω = 1,414.r.ω
- vD = 2.r.ω
telkens loodrecht op de verbindingslijn met A. (De beweging van A als punt van het wiel is een cycloïde. Een grafiek hiervan wordt op het einde van de volgende paragraaf gegeven.)
Deze aanpak is echter veel algemener bruikbaar. De vlakke beweging van elk onvervormbaar voorwerp kan beschreven worden als een ogenblikkelijk roteren rond een bepaald punt. Laat 2 snelheden van een voorwerp gegeven zijn, nl. de snelheid vA van het punt A en vB van het punt B, beiden in hetzelfde bewegingsvlak. De snelheid van het punt B kan niet willekeurig verschillen van die van A. Vanuit A bekeken moet vB gelijk zijn aan vA plus het effect van een rotatie van het voorwerp rond A. Een lineaire snelheid die ontstaat doordat het punt B roteert met hoeksnelheid ω rond een as door A kan geschreven worden als:
Hierbij staat de vector ω loodrecht op het bewegingsvlak van A en B. De snelheid vA kan natuurlijk altijd geschreven worden als veroorzaakt door een rotatie rond een punt P zodat vA = ω * PA of vectorieel: . De vraag is nu of de snelheid vB ook kan geschreven worden als het effect van een rotatie rond hetzelfde punt P met zelfde ω .
Uit vorige blijkt:
Het is dus steeds mogelijk om ook de snelheid van elk ander punt van het voorwerp te schrijven als het effect van een rotatie rond het ogenblikkelijk rotatiecentrum P. Een meer algemeen bewijs kan gegeven worden na de studie van het samenstellen van rotaties.

Deze methode van het ogenblikkelijk rotatiecentrum wordt vooral gebruikt in de studie van stangenmechanismen. De methode wordt meestal gekoppeld aan een grafische benadering van het probleem. Ingenieuze grafische oplossingsmethodes voor veel problemen waren zeer gebruikelijk tot de opkomst van de zakrekenmachine en de PC. Voor deze grafische aanpak steunt men op het feit dat de snelheid altijd loodrecht moet staan op de straal vanuit het rotatiecentrum. Er is vereist dat men van één punt de snelheid volledig kent en van een ander de richting. Men construeert dan in elk punt een loodlijn op de richting van de snelheid. Het snijpunt van beide loodlijnen geeft het ogenblikkelijk rotatiecentrum. Uit de bekende snelheid haalt men dan de bijhorende hoeksnelheid.
Als voorbeeld hierboven een klassiek kruk- en drijfstangmechanisme. In dat voorbeeld leidt een loodlijn op de snelheid van B en C tot een snijpunt in D. Uit vB = BD.ω en vC = CD.ω volgt dan:
- vB/vC = BD/CD
Hierin zal CD en BD moeten berekend worden uit BC of AC en de hoek in C. Tenslotte kan men dan schrijven dat ωA = vB/AB
Bij een translatie zal de snelheid van A en B gelijk zijn. Men kan dit beschouwen als het effect van een rotatie rond een punt op oneindig. Men zal dan twee evenwijdige loodlijnen hebben, waarvan het snijpunt op oneindig valt. Wanneer stangenmechanismen niet scharnierend maar via pin en gleuf met elkaar verbonden zijn, is er nog een meer klassieke benadering via relatieve en sleepsnelheid nodig in die verbinding om het correcte verband tussen de snelheden van pin en gleuf te berekenen.

Bij een auto die een bocht neemt, ligt het ogenblikkelijk rotatiecentrum in het verlengde van de achteras. De voorwielen volgen dus een grotere cirkel dan de achterwielen. Dat leidt vooral tot problemen bij lange voertuigen. Op sommige bussen en aanhangwagens ziet men achteraan de tekst: "Opgelet: zwenkt uit". Dit zijn voertuigen die uitgerust zijn met gestuurde achterwielen. Deze worden in tegengestelde zin van de voorwielen gedraaid, waardoor ze beter in het spoor van de voorwielen volgen en kortere bochten mogelijk maken. Men noemt ze daarom ook wel "spoorvolgers". Het ogenblikkelijk rotatiecentrum schuift dan iets naar rechts en ligt dan meer symmetrisch t.o.v. voor- en achteras. Ook sommige personenwagens hebben achterwielen die lichtjes gestuurd worden. Bij lage snelheid en scherpe bocht draaien ze ook iets naar buiten. Bij hoge snelheid en kleine verdraaiing van het stuur, zoals bij het veranderen van rijstrook op een snelweg, sturen ze mee met de voorwielen. Hierdoor wordt een stukje translatie gebruikt om de verandering van rijstrook uit te voeren, waardoor er minder rotatie en kleinere middelpuntzoekende krachten nodig zijn.
Een iets ingewikkelder voorbeeld is het uitwendig rollen zoals in de figuur hiernaast. Een rol 2 wordt via een staaf die draait rond A met hoeksnelheid ωstaaf, verplicht te rollen over de stilstaande rol 1. Gevraagd wordt de hoeksnelheid van rol 2.

Als de rol 1 stilstaat, moet het contactpunt C tussen beide rollen het ogenblikkelijk rotatiecentrum zijn van rol 2. Voor de snelheid van B kan men dan schrijven:
- vB = r2.ω2
Anderzijds kan men B bekijken als een punt van de staaf. Dan geldt:
- vB = AB.ωstaaf
Hieruit vindt men het verband:
- ω2 = (AB/r2)ωstaaf
Indien de rol 1 ook zou roteren in wijzerzin, dan zou men weer de snelheid van het punt C moeten bekijken vanuit A en vanuit B en kan men schrijven:
- vC = r1.ω1 = AB.ωstaaf - r2.ω2
Het fysische punt van het bewegend voorwerp dat op een bepaald ogenblik het rotatiecentrum is, staat op dat ogenblik stil, maar was voor- en nadien in beweging. Het heeft dus een versnelling. Deze wordt in volgende paragraaf berekend.
Poolbaan en poolkromme
[bewerken]Bij het spreken over het ogenblikkelijk rotatiecentrum moet men 2 punten onderscheiden:
- het punt van het voorwerp dat op een bepaald ogenblik het rotatiecentrum is. Men noemt dit ook wel het rotatiecentrum als fysisch punt.
- het punt dat bepaald wordt door de eigenschap "rotatiecentrum zijn" en dat elk ogenblik een ander punt is (tenzij bij rotatie rond een vast punt of as). Men zou dit het rotatiecentrum als logisch punt kunnen noemen.
Tijdens de beweging beschrijft dit logisch punt een baan binnen het vast systeem en t.o.v. het bewegend voorwerp. Bij een wiel dat over een rechte rolt bv., is die rechte de baan binnen het vaste systeem en vormt de omtrek van het wiel de baan t.o.v. het bewegend voorwerp. De eerste baan noemt men de poolbaan, de tweede de poolkromme.
- Poolbaan: de baan gevormd door de opeenvolgende rotatiecentra binnen het vaste referentiesysteem.
- Poolkromme: de baan gevormd door de opeenvolgende rotatiecentra t.o.v. het bewegend systeem.
Beide banen hebben steeds het ogenblikkelijke rotatiecentrum gemeen en raken elkaar in dat punt. Een vlakke beweging van een voorwerp kan daarom beschreven worden als een rollen van de poolkromme over de poolbaan.

Een iets meer ingewikkeld voorbeeld wordt gegeven in de figuur hiernaast. De uiteinden van de staaf AB worden daarin verplicht te glijden langs 2 loodrecht op elkaar staande wanden. De poolbaan is dan een kwart van de cirkel vanuit het hoekpunt en met straal AB. De poolkromme is een cirkel met AB als diameter. De driehoek AOB is immers altijd een rechthoekige driehoek met AB als schuine zijde. Nu is de schuine zijde van een rechthoekige driehoek ook altijd de diameter van de omschreven cirkel. De beweging van de staaf kan hier ook beschreven worden als het inwendig rollen van de poolkromme langs de poolbaan. Het punt dat op een bepaald ogenblik rotatiecentrum is, valt alleen in de twee uiterste standen van de staaf ook op de staaf. Wanneer men hier over het roatiecentrum als fysische punt spreekt, dan bedoelt men de positie van het punt in een referentiesysteem dat vast verbonden is aan de staaf. Dat punt heeft binnen dat systeem een onveranderlijke positie t.o.v. de staaf.
De snelheid waarmede het rotatiecentrum als logisch punt zich verplaatst over de poolbaan en de poolkromme noemt men de poolververplaatsingssnelheid vP. Daar het rotatiecentrum een gemeenschappelijk punt is van poolbaan en poolkromme en deze in dat punt niet bewegen t.o.v. elkaar (er is geen slippen van de ene kromme over de andere) is deze snelheid dezelfde langs beide krommen. M.a.w. in zelfde tijd wordt altijd de zelfde afstand afgelegd langs beide krommen. Men kan bewijzen dat de versnelling van het rotatiecentrum aOR als fysisch punt bepaald is door:
Let op de volgorde van de termen! Deze versnelling zal steeds naar het kromtemiddelpunt van de poolkromme gericht zijn. Daar ω en vP steeds loodrecht op elkaar staan, is de grootte van aOR = ω.vP.
Voor een wiel dat over een rechte rolt is vP = vC, de snelheid van het centrum van het wiel. De versnelling van het contactpunt met de grond is naar het centrum van het wiel gericht en heeft als grootte:
- aP = ω.vP = r.ω2
Tot dezelfde conclusie kan men komen als men de versnelling van het contactpunt met de grond wil berekenen vanuit het centrum van het wiel (in de onderstelling van een constante snelheid van dat centrum = r.ω):
Hierin is echter aC = 0 en ook a(P,C)t = 0 (geen hoekversnelling, dus geen tangentiële versnelling). Er blijft dus alleen een relatieve normale versnelling = r.ω2.
Het contactpunt met de grond beschrijft, als fysisch punt van het wiel, een een cycloïde. Men ziet op de grafiek hieronder duidelijk hoe het fysisch punt in de onderste stand tot stilstand komt en dan opnieuw vertrekt in de andere richting. Het onderste punt van de kromme wordt daarom een keerpunt van de kromme genoemd. Door y 2x te differentiëren naar de tijd, kan men gemakkelijk controleren dat ay van het punt dat de grond raakt (bij φ=0 of 2nπ) gelijk is aan rω2 en dat een eventuele hoekversnelling (2e afgeleide van φ) hierop geen invloed heeft.

Een iets intrigerender voorbeeld wordt gevormd door een lat die rond een paal draait of een bolletje aan het einde van een touw dat men zo lanceert dat het touw opgewonden wordt rond een paal. Bij de lat rond de paal is de omtrek van de paal nu de poolbaan en de zijkant van de lat de poolkromme. De versnelling van het ogenblikkelijk rotatiecentrum is van het centrum van de paal weg gericht. Bij het bolletje blijkt dat er alleen een versnelling is in de richting van het touw, wat overeenkomt met de wet van Newton.

Voor de behandeling van dit voorbeeld is kennis van het hoofdstuk Elementaire dynamica vereist.
Men kan de versnelling van het bolletje berekenen met de vereenvoudigde formule uit het hoofdstuk over de versnelling. Dan moet men schrijven dat
waarin, met l actuele lengte van het touw tussen bolletje en paal:
- aOR = r.ω2 want vP = r.ω
- ar,n = relatieve normale versnelling = l.ω2
- ar,t = relatieve tangentiële versnelling = l.α
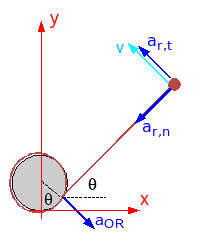
De vraag is nu wat het verband is tussen ω en α ?
- Er is hier geen behoud van impuls. De richting van de snelheid verandert voortdurend en dus ook de impuls.
- er is geen behoud van impulsmoment. Voor de berekening van het impulsmoment moet men natuurlijk altijd hetzelfde punt gebruiken, bv. het middelpunt van de paal. Dan heeft de spanning in het touw een moment t.o.v. dit punt en is er dus een wijziging van het impulsmoment.
- er is wel behoud van energie. De spanning in het touw staat loodrecht op de snelheid. Er is dus geen toevoer of afvoer van energie door de kracht in het touw. Als men de beginsnelheid aanduidt met v0, dan moet op elk ogenblik gelden:
- m.v02/2 = m.v2/2
Hieruit volgt ook dat v0 = v, of m.a.w. dat de grootte van de lineaire snelheid v constant is. Daar op elk ogenblik geldt dat v = l.ω = l0.ω0 is dus ook l.ω constant. Differentiëren hiervan leidt tot:
Of:
Het minteken zegt dat als l afneemt, α moet toenemen. l wordt steeds kleiner omdat het touw oprolt rond de paal.
Uit differentiëren van l = l0 - rθ volgt dl/dt = -r.ω. Dat invullen in vorige formule levert:
Er geldt dus aOR = ar,t, maar beide hebben tegengestelde zin. Ze vallen dus tegen elkaar weg en er blijft alleen de ar,n.
Men kan het gebeuren ook beschrijven in een klassiek cartesisch assenkruis.
Differentiëren levert, met dl/dt = -r.ω:
Uit het behoud van energie volgde dat l.ω = l0.ω0 of
Hieruit blijkt duidelijk dat de snelheid loodrecht staat op het touw en constant is. Voor de versnelling vindt men:
Waaruit blijkt dat de versnelling op haar beurt loodrecht staat op de snelheid en er dus alleen een versnelling blijft volgens het touw.
Samenstellen van rotaties
[bewerken]Onze handen hangen aan onze schouder vast via het polsgewricht, de onderarm, het ellebooggewricht, de bovenarm en het schoudergewricht. Geen enkele van die gewrichten laat een schuifbeweging toe, maar toch hebben we er geen enkel probleem mee om onze hand volgens een rechte lijn te laten bewegen. Dit resultaat wordt bekomen door het samenstellen van rotaties in de verschillende gewrichten.
Er is echter een eigenaardig verschil tussen hoeksnelheden en -versnellingen en een rotatie over een reële hoek. Alhoewel men dit laatste ook als een vectorpijltje zou kunnen voorstellen volgens de conventies voor de hoeksnelheid, vormen eindige rotaties geen vectoren omdat ze niet commutatief zijn. Dit kan gemakkelijk aangetoond worden bv. in de figuur hieronder. Het gaat hierbij over rotaties rond assen die elkaar snijden in één punt.

In het bovenste voorbeeld wordt een voorwerp eerst over 90° gedraaid volgens de x-as, dan over 90° volgens de y-as. In het onderste wordt eerst rond de y-as gedraaid en dan rond de x-as. Men ziet duidelijk dat het resultaat totaal verschillend is. Een rotatie zoals hierboven kan wiskundig weergegeven worden in een rotatiematrix. Het is wel bekend dat het product van 2 matrices normaal niet commutatief is.
Hoeksnelheden kunnen wel als vectoren behandeld worden. Men kan hiervoor een ingewikkeld wiskundig bewijs leveren via de commutativiteit van de betrokken matrices. Meestal wordt een eenvoudige "bewijs" geleverd door het beschouwen van de verplaatsingen in een infinitesimaal interval dt. Elk punt van een voorwerp krijgt dan een verplaatsing dri onder invloed van een ωi volgens de formule:
De som van deze dri is wel commutatief, zodat het resultaat ook kan geschreven worden als
Dat de de beweging van het voorwerp kan beschreven worden als het uitvoeren van een ogenblikkelijke rotatie die de som is van alle deelrotaties, volgt ook uit de meer algemene theorie die verder ontwikkeld wordt.
Rotaties op meerder niveaus
[bewerken]
De figuur hiernaast stelt een plateau voor dat draait rond een verticale as. Op dat plateau staat een motor, die zelf kan draaien rond een horizontale as. Deze motor doet een schijf draaien. Gevraagd wordt de snelheid van het punt P op de rand van de schijf.
Men zou dit kunnen oplossen met de techniek van de samengestelde beweging, zoals beschreven in Kinematica 2: bewegende referentiesystemen. Men zit hier echter met 3 niveaus van beweging, zodat men minstens 2x samengestelde beweging zou moeten toepassen. Men kan hier een andere aanpak volgen. Als men onderstelt dat er alleen een ω1 is, dan wordt de snelheid van P gegeven door
waarin de vector rP1 de positie van het punt P voorstelt t.o.v. een willekeurig punt van de as waarrond ω1 draait, hier dus de as van de motor. Dat dit punt een willekeurig punt mag zijn, werd aangetoond in het 1e hoofdstuk over elementaire bewerkingen met vectoren, in de paragraaf over het verband tussen hoeksnelheid en lineaire snelheid.
Wanneer men ook ω2 in rekening brengt, dan kan men de rotatie van de schijf beschouwen als een relatieve beweging binnen een assenkruis verbonden met de motor en draaiend met hoeksnelheid ω2. Bij de snelheid van P, zoals hierboven berekend, komt dan een sleepsnelheid die analoog kan berekend worden:
De totale snelheid van P wordt dan:
Wanneer men nu ook ω3 in rekening brengt, dan kan men deze snelheid van P weer beschouwen als een relatieve snelheid binnen een assenkruis verbonden met de schijf. Er komt dan weer een sleepsnelheid bij die het effect is van ω3 en het totale resultaat kan weer geschreven worden als:
Hiermede heeft men een formule om de lineaire snelheid uit te rekenen van een punt dat onderworpen is aan een reeks rotaties.
Equivalentie van rotaties
[bewerken]Wanneer men in bovenstaand voorbeeld de beweging van de schijf wil bestuderen, dan moet men de hoeksnelheid en hoekversnelling van de schijf kennen t.o.v. assen door het massacentrum en de versnelling van dat massacentrum. Dit komt neer op de vraag om een equivalent systeem van rotaties samen te stellen in dat massacentrum. Bij het opstellen van een equivalent vectorsysteem, gaat het over een systeem van wat men basiselementen zou kunnen noemen en een stel van vectoren dat daarmee verbonden is via een vectorieel product van een positievector en één van deze basiselementen. Bij het samenstellen van krachten waren de basiselementen de krachten en de afgeleide vectoren de momenten. Hier zijn de basiselementen de hoeksnelheden en de afgeleide elementen de lineaire snelheden. De berekening van de lineaire snelheid van het punt P onder invloed van 3 rotaties, is dus analoog aan het berekenen van het moment in een punt P veroorzaakt door 3 krachten.
Een systeem van rotaties kan herleid worden in een punt P tot een equivalent systeem bestaande uit een hoeksnelheid en de lineaire snelheid van het referentiepunt P:
* * met rPi de positie van P t.o.v. ωi

Deze besluiten kunnen nu eens toegepast worden op de bovenstaande figuur. Hiervoor zijn dan wel enkele afmetingen en hoeken nodig. Men onderstelt dat de as van de motor radiaal ligt, d.i. door de vertikale as wijst. Men heeft de volgende projecties in het gegeven assenkruis:
- ω1 = ( 0, -ω1.cos θ, -ω1.sin θ)
- ω2 = (ω2,0 ,0)
- ω3 = ( 0, 0, ω3)
Hiermede bekomt men als resulterend ω:
- ω = (ω2, -ω1.cos θ, ω3 - ω1.sin θ)
Voor de posities van P vanuit de verschillende rotatievectoren:
- rP1 = ( 0, -r.sin θ, r.cos θ)
- rP2 = ( 0, l2.cos θ - r. sin θ, l2.sin θ + r.cos θ)
Voor de laatste positie wordt gewoon de loodrechte afstand gebruikt:
- rP3 = ( 0, l1 + l2.cos θ - r. sin θ, 0)
Hiermede kan men de verschillende bijdragen aan de snelheid van P uitrekenen:
De som van deze 3 componenten levert de totale snelheid van P. Voor de duidelijkheid wordt deze opgesplitst in haar cartesische componenten:
Om de idee van equivalent systeem toch nog eens duidelijker te maken, wordt de snelheid van P ook eens berekend in 2 stappen. Eerst wordt het systeem herleid tot een equivalent systeem in O, het midden van de motor en het snijpunt van ω1 en ω2. Vandaar zal dan opnieuw de snelheid van P berekend worden.
Waarom het punt O? Omdat de lineaire snelheid van dat punt eenvoudig uit te rekenen is. Daar het punt op het snijpunt van ω1 en ω2 ligt, hebben deze rotaties geen invloed op vO. Die wordt alleen beïnvloed door ω3:
- vO = (-l1.ω3, 0, 0)
De resulterende ω blijft dezelfde als hierboven. De positie van P t.o.v. O wordt:
- rPO = ( 0, l2.cos θ - r. sin θ, l2.sin θ + r.cos θ)
De snelheid van P moet nu berekend worden volgens de formule:
In cartesische componenten levert dit (alleen de x-component is wat ingewikkeld):
...wat precies hetzelfde is als eerst. Hiermede is dan ook aangetoond dat het systeem in O equivalent is met het originele systeem.
Bij een robot zal men moeten eisen dat het equivalente systeem in de actuator bestaat uit een bepaalde lineaire snelheid en een bepaalde hoeksnelheid.
Speciale gevallen
[bewerken]1. Samenlopende rotaties
Wanneer de verschillende rotatievectoren door één punt passeren, dan kunnen ze in dat punt samengesteld worden tot een equivalent systeem bestaande uit één rotatievector, zonder een lineaire snelheid van het herleidingspunt. Zie verder voor toepassingen in combinatie met rollen.
2. Evenwijdige rotatievectoren
Wanneer alle rotatievectoren onderling evenwijdig zijn, dan is er ook een herleiding mogelijk tot één rotatievector, zonder een lineaire snelheid van het herleidingspunt, in een punt dat men het zwaartepunt van het systeem zou kunnen noemen. Dit wordt weinig toegepast. Men kan die resulterende vector ook zien als de ogenblikkelijke rotatieas.
3. Koppel van rotaties

Wanneer een systeem onderworpen is aan twee even grote en evenwijdige rotaties, maar met tegengestelde zin, dan is het resultaat een translatie. In elk punt levert dit immers een equivalent systeem dat alleen bestaat uit een lineaire snelheid. Als men onderstelt dat het rad hiernaast in wijzerzin rond zijn as draait, dan zal elk kabientje in tegenwijzerzin rond zijn ophangpunt draaien. Het resultaat is dat de kabientjes transleren (kromlijnige translatie!). Typisch voor translatie is dat richting behouden blijft. Vloer en dak blijven horizontaal, de wanden blijven steeds verticaal.
4. Schroefas
Men kan ook voor een systeem van rotaties zoeken naar een lijn waar de lineaire snelheid evenwijdig is met de resulterende hoeksnelheid volgens de formule ω = kv.
Lineaire versnellingen en hoekversnellingen
[bewerken]Bij het afleiden naar de tijd van de bovenstaande uitdrukkingen moet men er rekening mee houden dat elke vector a die gedefinieerd is t.o.v. een systeem dat roteert met hoeksnelheid ω ook een "sleepverandering" ondergaat van de vorm ω x a (zie Een nieuwe operator).
Bij afleiden van de resulterende ω in het bovenstaande voorbeeld zal men dus krijgen:
Voor de lineaire versnelling van het referentiepunt geldt dan:
- met
waarbij de afgeleiden van de ωi moeten berekend worden volgens de besproken methode. Maar iets analoogs geldt voor het afleiden van rPi:
waarbij j loopt over alle rotatievectoren waaraan rPi onderworpen is. Een behoorlijke boterham!
Rollen
[bewerken]Wanneer twee voorwerpen over elkaar rollen, is er een lijn van punten die een gemeenschappelijke snelheid hebben. Op deze lijn zal ook de ogenblikkelijke relatieve rotatievector liggen. Wanneer één der voorwerpen stilstaat is dat ook de absolute ogenblikkelijke rotatievector.

Als voorbeeld het geval van tandwielen tussen twee loodrecht op elkaar staande assen, zoals schematisch voorgesteld hiernaast. Het ene tandwiel is klein, het andere groot. Dit is bij auto's bekend als het systeem van pignon en kroonwiel. Men kan het in elkaar grijpen van de tanden zien als het over elkaar rollen van de twee tandwielen. De hoeksnelheid van het grote tandwiel moet hierbij de som zijn van de hoeksnelheid van het kleine (ω1) + de hoeksnelheid waarmede het grote over het kleine rolt (ω21). Voor een zuiver rollen moet de lijn van de tanden, de richting van ω21, dus door het snijpunt van de 2 assen wijzen. Daar kan het systeem immers samengesteld worden tot 1 zuivere resulterende rotatie en beantwoorden de 3 rotaties dan aan de vectoriële driehoek die in de figuur gegeven is.
Bij de externe fietsdynamo, die met een wieltje tegen de band aangedreven wordt, zal men moeten zorgen dat de as van die dynamo door (het verlengde van) de as van het wiel wijst opdat het wieltje zuiver over de band zou rollen zonder er langs te wrijven.









































