Klassieke Mechanica/Voorwerpendynamica-2
Algemene rotatie
[bewerken]Inleiding
[bewerken]Hiervoor werd het geval besproken van de rotatie rond een as met vaste richting. Deze as mag bewegen, maar hij mag niet veranderen van richting. Het werd daar eendimensionale rotatie genoemd. Het is absoluut nodig dat men het begin van dat eerste deel gelezen en begrepen heeft om dit vervolg te kunnen begrijpen. De algemene of driedimensionale rotatie is immers veel ingewikkelder dan de eendimensionale, om verscheidene redenen. Vooreerst speelt alles zich af in 3 dimensies. Die moeten in een perspectieftekening voorgesteld worden. Wie weinig ruimtelijk inzicht heeft, kan hiermede problemen hebben. Vervolgens gedragen de systemen die hier beschouwd worden, zich absoluut niet zoals men intuïtief verwacht. En tenslotte moet men om alles in formules te gieten beroep doen op meer gevorderde wiskunde, zoals vectoriële producten en matrices. Normaal behoort deze stof tot de universitaire opleidingen. Er zal toch geprobeerd worden om aan iedereen enig inzicht in de fenomenen te geven.

De figuur hiernaast geeft een eenvoudig voorbeeld van een situatie waarbij de eendimensionale aanpak niet meer werkt. De rotatie-as van het wiel verandert voortdurend van richting. Dit valt dus niet onder de vorige formules.
Basiswet
[bewerken]Men kan het rechterlid van de wet van Newton schrijven als m.a, maar ook als de afgeleide van de impuls p = m.v als:
Op analoge manier is de basiswet voor de rotatie te schrijven als (afleiding infra):
- de som van de momenten van de uitwendige krachten moet gelijk zijn aan de verandering van het impulsmoment.
Bij de eendimensionale rotatie moet men het moment nemen van alle krachten t.o.v. de rotatie-as. Hier moet men het moment nemen t.o.v. een punt P. Dit punt moet een stilstaand punt zijn of het massacentrum. Er is nog een derde mogelijkheid, nl. een punt waarvan de snelheid evenwijdig is aan de snelheid van het massacentrum. Dit is meestal maar een tijdelijke situatie, die niet kan gebruikt worden voor het opstellen van differentiaalvergelijkingen. Daarom wordt ze meestal niet vermeld. Voor de eenvoud van de formules voert men normaal een assenkruis in zodat dat punt P de oorsprong van het assenkruis is. Het moment van een kracht wordt dan gegeven door het vectoriële product van de positievector van het aangrijpingspunt van die kracht met de kracht.
De praktische berekening van het rechterlid wordt verder hieronder nog uitgewerkt.
Afleiding
Voor één massa zegt de wet van Newton:
Wanneer men het moment neemt van beide leden t.o.v. de oorsprong dan bekomt men nog altijd een gelijkheid want de positievector voor het linker en het rechterlid is dezelfde:
Wanneer men een verzameling van puntmassa's beschouwt, de wet van Newton op elke massa toepast en dan het moment neemt van beide leden en alles lid aan lid optelt, bekomt men:
- (1)
Men zou normaal een dubbele som moeten invoeren voor de krachten, maar men kan het ook bij één som houden, waarbij sommige ri dezelfde zullen zijn. Bedenk dat de index i in het linkerlid niets te maken heeft met de index i in het rechterlid. De krachten kan men verdelen in uitwendige en inwendige krachten, d.i. krachten tussen de massa's onderling. De inwendige krachten vormen actie-reactiekoppels, die op dezelfde drager liggen. Daardoor valt het moment van de krachten in elk koppel tegen elkaar weg. Men moet dus alleen rekening houden met de uitwendige krachten.
Anderzijds zou men het rechterlid willen schrijven als de afgeleide van het impulsmoment L, nl. . Als men hiervan de afgeleide neemt, dan bekomt men twee sommen. De vraag is nu in welke gevallen dit zich herleid tot één som zoals in de betrekking hierboven. Om dit volledig algemeen te bekijken, kan men het moment nemen t.o.v. een willekeurig punt P, dat niet noodzakelijk moet stilstaan. Als rP de positievector is van P t.o.v. de oorsprong en ri de positie van het i-de punt t.o.v. de oorsprong, dan is de positie van dit punt t.o.v. P gegeven door:
En het impulsmoment t.o.v. P wordt:
Als men dit differentieert krijgt men:
De eerste term kan uitgewerkt worden in 2 termen:
Hierin is
- de eerste term = 0 want een vectorieel product van een vector met zichzelf is 0.
- De tweede term is zeker ook 0 als P een stilstaand punt is. Bemerk dat het geen belang heeft of P een versnelling heeft, alhoewel men in dat geval het punt alleen kan gebruiken voor een ogenblikkelijke berekening en niet voor het opstellen van een differentiaalvergelijking.
- De tweede term is ook 0 als de snelheid van P evenwijdig is aan de snelheid van het massacentrum. Uit de definitie van het massacentrum volgt immers :
- De tweede term is tenslotte ook 0 als P het massacentrum is. Dan is immers . De term is dan de relatieve positie van elk punt t.o.v. het massacentrum. Dit zal hier opnieuw aangeduid worden als .
In de laatste term staan nu nog de afgeleiden van de absolute snelheden. Het zou logischer zijn om voor het impulsmoment ook te werken met de relatieve snelheden. Het blijkt dan men bij het berekenen van het impulsmoment t.o.v. het massacentrum, zowel met de absolute als met de relatieve snelheden mag werken. Men heeft:
De eerste term hierin is 0 want bij positiebepaling t.o.v. het massacentrum geldt:
Einde van de afleiding
Traagheidstensor
[bewerken]De notie van impulsmoment kwam ook reeds voor bij eendimensionale rotatie hierboven. Daar werd het impulsmoment geschreven als L = Iω. In het algemene geval moet men teruggrijpen naar de definitie als som van de momenten van de impulsen van alle (punt)massa's t.o.v. een punt:
Bij een onvervormbaar voorwerp kan men die vi schrijven in functie van de hoeksnelheid ω m.b.v. een vectorieel product als
Als men dat invoert in de vorige formule (zie afleiding infra) krijgt men een resultaat dat kan voorgesteld worden, mits de complexiteit een beetje te verschuiven, als:
De 3 x 3 matrix noemt men de traagheidstensor. Men spreekt van een tensor omwille van de manier waarop de elementen veranderen bij verandering van het assenkruis (zie hiervoor het laatste deel van dit hoofdstuk Transformaties van de traagheidstensor en de traagheidsellipsoïde). In elke element zit 2x een positie verwerkt, zodat de elementen bij bv. een rotatie van het assenkruis op een andere manier zullen veranderen dan de componenten van een vector. Deze traagheidstensor kan gevisualiseerd worden als een ellipsoïde. Zie op het einde van dit hoofdstuk Gyratiestraal - Traagheidsellipsoïde
Afleiding: L als functie van ω
Voor een onvervormbaar voorwerp is het handiger om de hoeksnelheid ω van het voorwerp en de totale massa te kunnen gebruiken. Hiervoor wordt elke vi herschreven als . De impulsmomentvector wordt dan:
Voor de uitwerking kan men eerst ω x ri schrijven als vi. Men bekomt dan:
Op analoge manier is
Voor de x-component van L vindt men:
Op analoge manier krijgt men:
Men stelt:
- is het traagheidsmoment t.o.v. de x-as. De term tussen de haakjes is immers de loodrechte afstand van mi naar de x-as.
- is een traagheidsproduct.
en analoog voor de andere elementen. Het is duidelijk dat
Hiermede kan de uitdrukking voor L geschreven worden als een matrixproduct van een traagheidstensor I met de hoeksnelheid ω :
Deze traagheidstensor is een symmetrische matrix: . Soms worden de traagheidsproducten hier zonder minteken genoteerd. Dan wordt er een minteken ingevoerd bij de definitie ervan.
Einde van de afleiding
Het is altijd mogelijk om een assenkruis te kiezen, vast verbonden aan het voorwerp, zodat deze matrix vereenvoudigd wordt tot een diagonaalmatrix. Hiermede wordt L eenvoudig:
Het assenkruis waarin men deze eenvoudige vorm bekomt heet een hoofdtraagheidsassenkruis en de assen ervan zijn hoofdtraagheidsassen. In het voorbeeld hieronder werd een schuin assenkruis gebruikt omdat de assen dan hoofdtraagheidsassen zijn. Hieronder worden de hoofdtraagheidsassen nog uitvoerig verder behandeld. Hoe deze herleiding kan uitgewerkt worden, wordt gepresenteerd in het laatste deel van dit hoofdstuk over Transformaties van de traagheidstensor en de traagheidsellipsoïde. Men vindt daar ook concrete voorbeelden van berekeningen van de elementen van een traagheidstensor.
Het traagheidsmoment uit de eendimensionale rotatie komt overeen met het element Izz, het traagheidsmoment t.o.v. de z-as. Het algemene geval is dus minstens 3x ingewikkelder dan het eendimensionale. Zie traagheidsmoment voor tabellen met de traagheidsmomenten van enkel voorwerpen.
Uit bovenstaande formule volgt ook dat indien volgens een hoofdtraagheidsas ligt, ook volgens dezelfde as zal liggen. Indien echter een willekeurige richting heeft, zal normaal niet meer dezelfde richting hebben als . Kijk bv. naar de situatie in het voorbeeld hieronder.
Een vector die ronddraait is een veranderende vector. Volkomen algemeen geldt dat, als de grootte van de vector ongewijzigd blijft maar de richting continu verandert, de vector ronddraait en de afgeleide loodrecht staat op die vector. Het meest bekende geval is de beweging met constante snelheid van een punt op een cirkel. De positievector van dat punt draait rond en de snelheidsvector is steeds loodrecht op de positievector. Hier draait de impulsmomentvector rond. De afgeleide ervan zal de richting hebben van de snelheid van de top van deze vector en zal zelf ook mee ronddraaien met de impulsmomentvector. Deze situatie vraagt dus een voortdurende inwerking van een uitwendig moment volgens de afgeleide van de impulsmomentvector.
Deze elementen zijn voldoende om een reeks interessante effecten te bespreken.
Gyroscopisch effect
[bewerken]Er wordt even teruggekeerd naar de eerste figuur, het rollend wiel. Het impulsmoment heeft een component volgens de z-as veroorzaakt door ω2 en een component volgens de y-as veroorzaakt door ω1. De z-component is constant, alleen de y-component draait rond. De top ervan heeft, in de getekende stand, een snelheid evenwijdig aan de x-as en volgens de positieve zin ervan. Volgens de basiswet van de rotatie moet er een uitwendig moment geleverd worden in dezelfde richting en zin, dus loodrecht op L.
Op het wiel grijpen de volgende krachten aan:
- het gewicht in het massacentrum
- een tegengestelde kracht van de grond om die op te vangen.
De som van deze beide krachten is nul en men kan ze verder vergeten.
Er is ook nog een kracht nodig die het centrum van het wiel naar binnen trekt en zo de middelpuntzoekende versnelling kan veroorzaken. Deze levert geen moment t.o.v. de oorsprong.
Het uitwendige moment kan alleen geleverd worden door een koppel van supplementaire krachten, één van de grond op het wiel(omhoog) en één in de bevestiging in de oorsprong omlaag. Door de rotatie gaat het wiel dus harder op de grond drukken.

Wanneer men het wiel maar aan 1 zijde ondersteunt, krijgt men een zeer eigenaardige reactie (zie figuur hiernaast). Het gewicht en de reactie in het steunpunt vormen een koppel met moment M, voor te stellen als een vector die horizontaal en naar achter gericht is (rechtsdraaiende schroef). Volgens de basiswet moet de punt van de impulsmomentvector nu ook naar achter bewegen. Hij moet rond een verticale as beginnen draaien. Men noemt deze rotatie ook de precessie. Waar een wiel dat niet draait gewoon zou vallen, begint een draaiend wiel rond te draaien. Op het einde vindt men links naar video's van dit fenomeen.
Men krijgt zo de eigenaardige situatie dat een moment loodrecht op L een rotatie uitlokt die opnieuw loodrecht staat op L en M. Dit eigenaardige gedrag staat bekend als gyroscopisch effect. Men kan het ook beschrijven als het feit dat, als men een kracht uitoefent op de as van een snel draaiend voorwerp, de as niet zal draaien in de richting van de kracht maar in een richting loodrecht erop, nl. in de richting van het moment van de kracht.
Omgekeerd: als men een snel draaiend voorwerp doet draaien om een as loodrecht op zijn rotatieas, dan reageert het door te proberen weg te draaien volgens een rotatierichting loodrecht op beide. Dit kan men gemakkelijk zelf vaststellen. Als men een draaiend fietswiel vasthoudt aan de uiteinden van de as, met de as horizontaal, en men probeert het wiel te kantelen om de as verticaal te brengen, dan voelt men een eigenaardige reactie van het wiel. Als men probeert om één uiteinde omhoog en het ander omlaag te brengen, dan oefent men een koppel uit als op de figuur hiernaast. Het wiel zal proberen rond een verticale as te draaien. Normaal probeert men ogenblikkelijk om die ongewenste beweging te stoppen, wat betekent dat men nu horizontale krachten gaat uitoefenen op de as. Dat is precies wat nodig is om het wiel te doen kantelen, wat het dan ook zal doen.
Een snel draaiend voorwerp laat veel moeilijker zijn richting veranderen dan een niet-draaiend voorwerp: er moet een groter moment op uitgeoefend worden en in een andere richting. Daarom geeft men kogels en andere projectielen een draaiende beweging. Daarom ook geeft men aan een discus of een frishbee een roterende beweging mee.
Wanneer een fietser bij het nemen van een bocht naar de binnenzijde van de bocht leunt, dan veroorzaken zijn gewicht en de verticale reactie van de grond ook een koppel dat de fietswielen de bocht doet nemen. De wielen van een fiets draaien echter niet snel en wegen niet veel, zodat dit effect niet zo belangrijk is. De situatie is totaal anders bij motoren. Daar draaien de wielen wel snel en ze zijn veel zwaarder. Motorrijders gebruiken het gyroscopisch effect op 2 manieren: om hun motor te doen hellen en om hem de bocht te doen nemen. Vanaf snelheden boven de 40 km/u zal een motorrijder bij het ingaan van de bocht een duwtje geven op zijn stuur in tegengestelde richting van de bocht. Dit zal het voorwiel niet doen draaien maar wel doen kantelen volgens de langsas van de motor. Als de motorrijder dan mee gaat hellen, creëert hij opnieuw een koppel dat helpt om zijn motor door de bocht te draaien.
Het gyroscopisch effect zorgt ook voor supplementaire krachten op de lagers van de turbines van straalvliegtuigen als die een bocht nemen.
Het effect wordt natuurlijk ook gebruikt in gyroscopen voor automatische besturing en in het gyrokompas. Voor wie filmpjes en veel meer informatie wil over het gyroscopisch effect in allerhande toepassingen kan vertrekken van https://www.gyroscopes.org/
Trillende autowielen
[bewerken]
Wanneer men een nieuwe band laat zetten op een autowiel, dan wordt dat thans ook altijd uitgebalanceerd om te vermijden dat het wiel bij hoge snelheid gaat trillen. Waarvoor dit nodig is kan men begrijpen aan de hand van het tweede voorbeeld, de rechthoekige plaat die draait rond een diagonaal. De L-vector verandert voortdurend van richting en dat vraagt een moment loodrecht op de rotatie-as en de L-vector. Dit moment moet geleverd worden door 2 krachten in de lagers: de krachten FA en FB op de figuur hiernaast. Die krachten moeten meedraaien met de plaat.
Men kan de noodzaak van deze krachten ook begrijpen als men denkt in termen van middelpuntvliedende krachten (of traagheidskrachten). Wanneer de rechthoek draait, zullen de delen naast de as naar buiten willen bewegen alsof er een kracht FT1 en FT2 op werkt. Deze krachten moeten opgevangen worden door FA en FB. Men kan ook begrijpen dat als de plaat kon draaien rond haar middelpunt, ze zou draaien tot ze horizontaal ligt. Dan liggen de beide middelpuntvliedende krachten in elkaars verlengde en veroorzaken geen rotatie meer (moment is nul). Dan draait de rechthoek ook volgens een hoofdtraagheidsas en ligt L volgens de rotatie-as.
Conclusie: een voorwerp probeert altijd volgens een hoofdtraagheidsas te draaien. Als dat niet het geval is moeten er voortdurende krachten op uitgeoefend worden om het in de gevraagde positie te houden. Wanneer er enige elasticiteit is in de bevestiging zal dat aanleiding geven tot trillen of slingeren.
Bij een niet uitgebalanceerd wiel valt de hoofdtraagheidsas van het wiel niet samen met de rotatie-as (die dan natuurlijk horizontaal is). Door kleine gewichtjes toe te voegen kan men beide wel doen samenvallen en verdwijnt het trillen.
Soms is dit trillen gewild. In een trilwekker voor doven of slechthorenden laat men een excentrisch geplaatst schijfje snel ronddraaien. Dit levert op een eenvoudige, efficiënte en betrouwbare manier een trillen op van een doosje dat men onder het hoofdkussen plaatst.
Bemerk dat de theorie van de eendimensionale rotatie niets kan zeggen over dit trillen. Bij die theorie kijkt men immers alleen naar de componenten van de verschillende grootheden volgens de rotatie-as. Die theorie zegt niets over wat in de 2 andere dimensies gebeurt.
Hoofdtraagheidsassen
[bewerken]Hierboven werd de meest algemene vorm van de traagheidstensor gegeven met de formules voor de diagonaalelementen.
De nevendiagonaalelementen worden traagheidsproducten genoemd en worden berekend als:
of als
Deze tensor is een symmetrische matrix, d.i. Ixy = Iyx.
Men kan deze matrix visualiseren en dan bekomt men een ellipsoïde (voor een figuur: zie einde van dit hoofdstuk). Een omwentelingsellipsoïde is het volume dat men bekomt door een ellips rond een hoofdas te laten draaien. Het lijkt dus een beetje op een rugbybal. Een ellipsoïde heeft 3 symmetrievlakken die loodrecht op elkaar staan. De snijlijnen van deze vlakken vormen 3 symmetrieassen. Als men een assenkruis volgens deze assen gebruikt voor het opstellen van de vergelijking bekomt men de eenvoudigste vorm. Evenzo leidt het gebruik van deze assen om de traagheidstensor te bepalen tot de eenvoudige diagonaalvorm. Een traagheidstensor kan men dus altijd herleiden tot een diagonaalvorm door een gepast assenkruis te kiezen.
Wanneer een voorwerp zelf symmetrie-elementen bevat, dan kan men op basis daarvan een hoofdtraagheidsassenkruis vinden. De regels hiervoor zijn:
- elke symmetrie-as is een hoofdtraagheidsas, waar men ook de oorsprong kiest op die as;
- een as loodrecht op een symmetrievlak is een hoofdtraagheidsas als de oorsprong in het symmetrievlak ligt.
Om een assenkruis te gebruiken voor berekeningen volgens bovenstaande formules, moet de oorsprong van het assenkruis echter in het massacentrum vallen of in een stilstaand punt.
Men kan dit illustreren m.b.v. een homogene rechthoekige balk. Zulk een balk heeft drie symmetrievlakken, die 3 symmetrie-assen bepalen. Deze snijden elkaar in het massacentrum. Deze symmetrie-assen kan men dus gebruiken als hoofdtraagheidsassen
(eerste figuur). Wanneer men de oorsprong van het assenkruis horizontaal verplaatst naar A, dan blijft het een hoofdtraagheidsassenkruis: de y-as is een symmetrie-as, de x- en z-assen staan loodrecht op een symmetrievlak en de oorsprong ervan ligt in het symmetrievlak (figuur 2). Men kan de traagheidsmomenten volgens x- en z-as berekenen met de formule van Steiner uit de traagheidsmomenten voor de assen door het massacentrum. Voor de berekeningen hier is echter alleen het punt A bruikbaar want alleen dat is een stilstaand punt.
Wat gebeurt er als men het onderste hoekpunt als oorsprong neemt (figuur 3 hieronder)? Dat is een stilstaand punt, maar dan heeft men geen hoofdtraagheidsassenkruis meer. Alleen de x-as is nog een hoofdtraagheidsas. De x-as staat loodrecht op een symmetrievlak en begint in dat symmetrievlak. Dat betekent dat er voor elk punt met coördinaten (x,y,z) er een punt bestaat met zelfde y en z maar tegengestelde x. De traagheidsproducten met een x-coördinaat erin zullen dus 0 worden:
.
Enkel de traagheidsproducten Iyz = Izy zullen verschillen van 0. Men kan ze berekenen als (met h=hoogte, b=breedte en d=dikte van de balk):
De impulsmomentvector L wordt dan:

Deze impulsmomentvector heeft dus een y-component en zal dus ronddraaien met de balk.
Izz door het hoekpunt werd hierbij afgeleid uit Izz door het massacentrum m.b.v. de formule van Steiner . T.o.v. het massacentrum:
T.o.v. het hoekpunt:
Er is nog een andere manier om L te berekenen. Daar voor de totale impuls geldt , moet, volgens de verplaatsingsformule, L in het onderste hoekpunt gelijk zijn aan de L berekend in het massacentrum vermeerderd met het moment van de totale impuls in het massacentrum t.o.v. dat hoekpunt. In formules:
Met een totaal andere aanpak bekomt men precies hetzelfde als het vorige, zoals het hoort.
Nota
De betrekking
wordt ook dikwjls geschreven als
wat men dan leest als "totale impulsmoment = baanimpulsmoment + spin".
Het rechterlid: de afgeleide van L
[bewerken]Opdat de traagheidstensor onafhankelijk zou zijn van de tijd (tenminste bij onvervormbare voorwerpen), heeft men een assenkruis gebruikt vast verbonden aan het voorwerp. Als men de afgeleiden van de impulsmomentvector L berekent door differentiëren van de componenten in dat assenkruis, heeft men alleen de verandering van L binnen dat assenkruis. Men noemt dit de relatieve verandering. Om de absolute verandering te hebben, d.i. zoals iemand die ziet die buiten het assenkruis staat, moet men nog rekening houden met het feit dat de impulsmomentvector mee rond draait met het assenkruis, meegesleept wordt met de beweging van het assenkruis (Zie ook Kinematica 2: een nieuwe operator). Als een vector ronddraait beschrijft zijn eindpunt een cirkel. Bij een vlak systeem wordt de snelheid van een punt op een cirkel gegeven als r.ω . In 3 dimensies moet men een vectorieel product gebruiken: . Dit levert als uiteindelijke formule:
De tweede term in deze formule kan men de sleepverandering noemen.
De basiswet voor de driedimensionale rotatie wordt dan:
De uitwerking van deze formule in projecties op de 3 assen wordt de vergelijkingen van Euler genoemd. Ze kunnen ook via andere wegen bekomen worden. Ze worden hier niet gegeven omdat het efficiënter is om van de vectoriële vorm te vertrekken voor berekeningen. Men ziet dan veel sneller welke termen 0 zijn en wat de nuttige berekeningen zijn die men moet maken.
Bij de voorbeelden die tot nu toe gezien werden zijn de projecties van L in het bewegend assenkruis constant. De eerste term, de relatieve verandering is dus telkens 0. De sleepverandering wordt voor het voorbeeld van de rechthoek roterend rond een diagonaaal:
Daar Ixx groter is dan Iyy ligt dat resultaat volgens de negatieve z-as. De punt van L beweegt op het getekende ogenblik inderdaad naar achter.
Rotatiesymmetrie
[bewerken]
Er is één uitzondering op de regel dat het assenkruis meedraait met het voorwerp. Wanneer men een rotatiesymmetrisch voorwerp heeft, zoals het wiel in het 1ste voorbeeld, en dat voorwerp draait rond die symmetrie-as, dan zal men het assenkruis deze laatste rotatie NIET laten volgen. Het is duidelijk dat de traagheidsmomenten volgens de x- en z-as niet veranderen als het wiel draait. De massaverdeling t.o.v. die assen blijft dezelfde. Men bekomt dus reeds een constante traagheidstensor door het assenkruis alleen ω2 te laten volgen. De impulsmoment vector in dat assenkruis is:
Ook hier is de relatieve verandering 0 (de componenten zijn constant binnen het bewegend assenkruis zodat de projecties geen functie zijn van de tijd). De sleepverandering is:
En dat is een resultaat volgens de positieve x-as, zoals uit de figuur verwacht wordt. Bemerk dat Lz niet verandert want die component ligt volgens ω2.
Nota 1. Als men het assenkruis toch volledig zou laten meedraaien met het wiel, dan moet men wel bedenken dat enige ogenblikken na de getekende stand, de z-as niet meer verticaal omhoog en de x-as niet meer horizontaal zouden zijn. Beide zouden iets linksom gedraaid zijn. De vector ω2 blijft echter wel verticaal naar beneden gericht. Binnen het (bewegend) assenkruis moet men die dan beschrijven als een vector die met hoeksnelheid ω1 rond draait in het xz-vlak, maar in tegengestelde zin van ω1 (cfr. het complexere voorbeeld hieronder). Het is als met iemand in de trein die de indruk heeft dat het station weg rijdt i.p.v. zijn trein. Dan zouden er wel afgeleiden zijn van ω2 en dus een relatieve verandering van L. Deze termen zouden echter wegvallen tegen even grote maar tegengestelde termen in de sleepverandering. Het is dan natuurlijk efficiënter en veiliger om een aanpak te volgen waarbij deze termen nooit berekend worden. Dat gebeurt door het assenkruis niet te laten meedraaien met ω1.
Nota 2. De rotatie rond de symmetrie-as, hier ω1, noemt men de spilomwenteling (in het Engels : spin). In de literatuur wordt het verschil tussen de hoeksnelheid van een assenkruis dat volledig vast is aan het voorwerp of een assenkruis dat de spilomwenteling niet volgt, aangegeven door met een kleine ω of een grote Ω te werken. De hier gevolgde formulering met een ωassenkruis voor de sleepverandering dekt beide gevallen en is zelfverklarend.
Praktische aanpak
[bewerken]Problemen van rotatie in drie dimensies kan men best in de volgende volgorde aanpakken:
- Zoek een punt dat als oorsprong kan dienen voor het assenkruis verbonden met het voorwerp. Dat punt moet ofwel stilstaan ofwel het massacentrum zijn.
- Bepaal de richting van de assen. Als er symmetrie-elementen in het voorwerp zijn, zal men proberen hiervan gebruik te maken om een hoofdtraagheidsassenkruis te bekomen. Bij rotatie rond een as kan eventueel nog geschoven worden met de oorsprong over die as. Dat de traagheidstensor diagonaal zou zijn, is in feite niet zo belangrijk in de methode met matrixrekenen, die hier gevolgd wordt. Die traagheidstensor is in feite alleen nodig voor het berekenen van de impulsmomentvector L. Het voorbeeld hierboven toont dat men die ook via de verplaatsingsformule kan berekenen, zonder eventuele nevendiagonaalelementen te moeten berekenen.
- Bepaal de totale ogenblikkelijke rotatievector en projecteer die op de assen van het gekozen assenkruis.
- Bereken de impulsmomentvector L op de klassieke methode (traagheidstensor x ogenblikkelijke rotatie) of een minder klassieke methode.
- Bereken de afgeleiden van L binnen het assenkruis, als die bestaan.
- Bereken de sleepverandering van L. Maak zo nodig een onderscheid tussen totale ogenblikkelijke rotatie en de rotatie van het assenkruis.
- Bereken de momenten van de uitwendige krachten t.o.v. de coördinaatassen
- Stop dit alles in de momentenvergelijking
- Pas zo nodig nog de wet van Newton toe, met in het rechterlid de totale massa en de versnelling van het massacentrum.
Er werd een interactief programma ontwikkeld om dit alles op een beknopte manier te presenteren en in te oefenen (voor Windows): rotatie32.zip
Kinetische energie - Behoud van impulsmoment
[bewerken]Kinetische energie
[bewerken]In het algemeen geldt (afleiding infra):
In functie van de traagheidstensor kan men schrijven:
Wanneer de traagheidstensor gediagonaliseerd is, wordt dit eenvoudig:
Afleiding
Men brengt ω voor het somteken door een cyclische permutatie naar links op dit "box product" (zie "box product" in eerste hoofdstuk) :
Voor een vrij bewegend voorwerp zal men opnieuw beroep moeten doen op de (2e) stelling van König (zie hoger massacentrum en energie):
- Ekin = kinetische energie van de translatie van het massacentrum (met totale massa) + kinetische energie van rotatie rond een as door het massacentrum.
Men kan dit nu eens toepassen voor de kinetische energie van de draaiende balk, die hoger gebruikt werd als voorbeeld bij hoofdtraagheidsassen en waarvan het impulsmoment enerzijds berekend werd in een hoofdtraagheidsassenkruis en anderzijds in een niet-hoofdtraagheidsassenkruis.
Voor het hoofdtraagheidsassenkruis in het massacentrum moet men dus opschrijven:
Voor het assenkruis in het punt linksonder:
Behoud van impulsmoment
[bewerken]Wanneer er geen uitwendige momenten op een voorwerp werken, dan kan het impulsmoment van dat voorwerp zich niet wijzigen (basisformule!). Er geldt dan een behoud van impulsmoment. De basisformule is echter een vectoriële wet en dan kunnen er soms geen uitwendige momenten zijn t.o.v. één bepaald richting. Dan geldt er een behoud van het impulsmoment t.o.v. die richting (of: van de projectie van het impulsmoment op die richting).
In de dagelijkse werkelijkheid ondervinden alle voorwerpen een aantrekkingskracht van de aarde. Verticale krachten hebben echter geen moment t.o.v. een verticale as. Er bestaat dan ook een vrij spectaculaire proef i.v.m. het behoud van impulsmoment in verticale richting. De proef is ook in verschillende "exploratoria" aanwezig.
De proef gebruikt een persoon die plaats neemt op een stoel (of plateau) die gemakkelijk kan draaien rond een verticale as (een geperfectioneerde bureaustoel). Men geeft aan de persoon een wiel, met een as met 2 stevige handvatten. Soms wordt een fietswiel gebruikt waarvan de velg met lood gevuld is om een groter traagheidsmoment te bekomen. De persoon houdt de as eerst horizontaal en men brengt het wiel vrij snel aan het draaien. Dan vraagt men de persoon om de as verticaal te brengen. Tot zijn grote verbazing zal hij in tegengestelde zin van het wiel beginnen draaien. Brengt hij de as weer horizontaal dan stopt hij. Draait hij de as in de ander richting naar de verticale stand, dan draait hij in de andere richting.
Verklaring
De enige uitwendige krachten die op de persoon en het wiel werken zijn aantrekkingskrachten van de aarde. Dat zijn verticale krachten en ze hebben dus geen moment t.o.v. de verticale as van de stoel. Ze kunnen m.a.w. geen rotatie rond de as op gang brengen of die rotatie op enige manier beïnvloeden. Bij het begin van de proef is het impulsmoment volgens een verticale gelijk 0: de persoon draait niet en het wiel heeft een horizontaal impulsmoment. De som van het impulsmoment van de persoon en de verticale component van het impulsmoment van het wiel, berekend t.o.v. de as van de stoel, moet dus steeds 0 blijven. Daarom gaat de persoon, met het wiel in de handen, in tegenovergestelde richting van het wiel beginnen draaien.
Het mechanisme hierachter is vrij eenvoudig. Uit het gedeelte over het gyroscopisch effect weet men dat er een verticaal moment moet uitgeoefend worden op het wiel om de as ervan rond een horizontale as te laten kantelen. De man moet met één hand trekken en met de andere duwen in een horizontaal vlak . De persoon ondervindt hierbij de reactie van het moment dat hij op het wiel uitoefent en begint daardoor zelf te draaien.
Om te berekenen hoe snel de man zal draaien, heeft men het impulsmoment van het fietswiel t.o.v. de as van de stoel nodig. Hiervoor moet men beroep doen op de formule dat voor een vrij bewegend voorwerp geldt:
met
- = baanimpulsmoment, d.i. impulsmoment van het massacentrum, waaraan men de totale massa van het voorwerp toekent;
- = impulsmoment t.o.v. een as door het massacentrum (S van "spin"). Hierbij moet gerekend worden met de absolute rotatie.
Zij hier:
- Iw : traagheidsmoment van het wiel t.o.v. zijn as
- ωw : hoeksnelheid van het wiel (bij het begin)
- mw : totale massa van het wiel
- Im : traagheidsmoment van man+stoel t.o.v. de as van de stoel
- ωm : hoeksnelheid van man+stoel
- d = afstand tussen as van het wiel (in verticale stand) en as van de stoel
De snelheid van met massacentrum is natuurlijk d.ωm .
Als de man de as van het fietswiel verticaal heeft moet dus gelden, na projectie op de verticale:
Een complexer voorbeeld
[bewerken]De momentenvergelijkingen
[bewerken]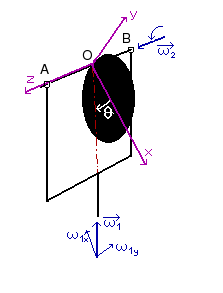
Als volgend voorbeeld wordt een schijf beschouwd die slingerend opgehangen is aan de rand ervan. Het geheel draait echter rond met een contante hoeksnelheid ω1.
Oplossing
Men voert een rechtsdraaiend assenkruis in dat een hoofdtraagheidsassenkruis is en waarvan de oorsprong stil staat. Om de positie van de schijf weer te geven moet men ook een hoek θ invoeren. Er zijn vele mogelijkheden om die te definiëren. Best werkt men van een as naar een bepaalde lijn, hier van de x-as naar de verticale. In eerste instantie wordt de hoeksnelheid van de schijf rond de as AB als ω2 aangeduid. Het verband met de afgeleide van θ wordt later bepaald.
De totale hoeksnelheid van de schijf:
De impulsmomentvector L wordt dan:
Het is duidelijk dat de projecties van ω1 voortdurend veranderen. In de formules komt dit tot uiting in het feit dat θ een functie is van de tijd. Er bestaan dus afgeleiden van de impulsmomentvector binnen het bewegend assenkruis:
Het is duidelijk dat de grootte van de afgeleide van θ overeenkomt met de grootte van ω2, maar niet noodzakelijk het teken. Dit laatste hangt af van de manier waarop θ gedefinieerd werd. Als θ hier toeneemt, dan krijgt men een rotatie in de zin van de positieve ω2. In dit geval kan men dus ω2 overal vervangen door om niet te veel onbekenden te hebben.
Om de absolute afgeleide van L te bekomen moet men nog de sleepverandering toevoegen:
De traagheidsmomenten (met r de straal en m de massa van de schijf):
Ixx = mr2/4 (uit de tabellen)
Iyy = mr2/4 + mr2 = 5mr2/4 (als vorige + Steiner)
Izz = mr2/2 + mr2 = 3mr2/2 (tabel + Steiner)
Hiermede kan men nu de absolute afgeleide van L berekenen:
- x-component:
- y-component:
- z-component:
De laatste term in de z-component kan men interpreteren als een middelpuntvliedende kracht, een zogenaamde traagheidsreactie (zie: Aanvullingen: Traagheidskrachten). Bij een gegeven θ beschrijft het massacentrum van de schijf een cirkel rond de vertikale met straal r.sinθ. Daarbij hoort een normale versnelling r.sinθ.ω12. Voor iemand binnen het roterend systeem lijkt het alsof er een naar buiten werkende kracht gelijk aan m.an werkt. T.o.v. de z-as heeft deze kracht een moment dat gelijk is aan r.cosθ.m.an. Het is echter eerder toevallig dat deze traagheidskracht in het massacentrum schijnt aan te grijpen. Dit moment is immers het resultaat van de som van de momenten van alle elementaire traagheidskrachten die op elk punt van de schijf aangrijpen, en die worden groter naarmate men zich van de as verwijdert.
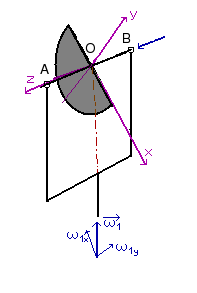
Het merkwaardige aan deze term is echter dat hij verdwijnt als Ixx = Iyy. Dat is het geval bij een halve schijf. Daar het traagheidsmoment een kwadratische functie is van de afstand tot de as, maakt het geen verschil uit of de twee kwartcirkelsegmenten aan tegengestelde zijden (zoals bij Iyy) of aan zelfde zijde van de as liggen (zoals bij Ixx). De frequentie waarmede deze halve schijf slingert wordt dus niet beïnvloed door ω1!

Om de volledige momentenvergelijkingen te kunnen opstellen moeten nu nog nog de momenten van de krachten berekend worden. Er zijn drie krachten: het gewicht en de reactiekrachten in A en B. Deze onbekende reactiekrachten worden beschreven met componenten volgens de assen. Volgens de z-as is er alleen een component in A en niet in B, anders wordt het syteem hyperstatisch. Men moet er wel aan denken dat, als de oplossing een constante component zou opleveren, dit betekent dat die component constant is in grootte maar mee beweegt met het assenkruis. De volledige momentenvergelijking geeft dan in projecties het volgende stelsel van 3 vergelijkingen:
- Stelsel I
De laatste vergelijking bepaalt het slingeren van de schijf. Ze kan vereenvoudigd worden tot:
Als men alleen in deze beweging geïnteresseerd is, dan zou deze vergelijking veel sneller en efficiënter kunnen bekomen worden met de methode van Lagrange Het is er uitgewerkt als derde voorbeeld. Als men de schijf loslaat met θ = 0 en in rust, dan gebeurt er niets. Als men de schijf loslaat met een relatieve beginsnelheid en/of bij een hoek θ > 0, dan zal de schijf beginnen slingeren. Daar niet alleen het moment van het gewicht speelt, maar ook iets dat men als een middelpuntvliedende kracht kan interpreteren, is de beweging zeker geen harmonische trilling. Men ziet dit duidelijk in de grafiek hieronder.
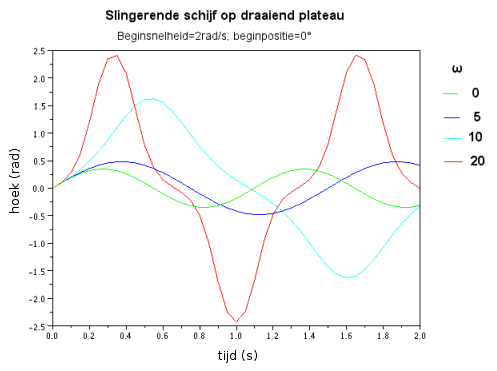

Indien er enige demping in het systeem aanwezig is, zal het naar een evenwichtstoestand gaan met relatieve hoekversnelling en hoeksnelheid = 0 en dus
Voor een beginsituatie met θ verschillend van 0 leidt dit tot de uitdrukking:
Voor kleine ω1 levert dit een uitdrukking die groter is dan 1. Voor die waarden zal het systeem evolueren naar θ = 0 en voor die positie is de bovenstaande afleiding niet geldig. Er is dus een minimun ω1 nodig vóór de schijf een schuine stand zal aannemen. Dit komt doordat de middelpuntvliedende kracht niet constant is, maar zelf functie is van θ. Men kan dit duidelijk zien in de grafieken hiernaast, waarin de coëfficiënt van sin(x)*cos(x) overeenkomt met r.ω12/g. Men ziet duidelijk dat deze coëfficiënt groter moet zijn dan 1 vooraleer er een snijpunt in het interval 0<x<90° mogelijk is (de x-as is in radialen, 90° = 1,57 rad). Dat snijpunt zal ook altijd vallen vóór x=1,57 rad (=90°) want voor die waarde gaat sin(x) naar 1 terwijl sin(x)*cos(x) er een nulpunt heeft.
Deel II: de wet van Newton
[bewerken]
Voor een volledige beschrijving van het syteem moet men nog de wet van Newton toepassen op de beweging van het massacentrum met daarin de totale massa van de schijf. Voor de versnelling van het massacentrum zal men moeten beroep doen op de volledige uitdrukking van de versnelling in een roterend systeem met een sleep-, relatieve en complementaire versnelling:
- De sleepversnelling bestaat hier alleen. uit een normale versnelling daar ω1 constant is:
- De relatieve versnelling heeft een normale en een tangentiële component:
- voor de complementaire versnelling is de relatieve snelheid nodig:
Hiermede wordt de complementaire versnelling:
Alles bij elkaar krijgt men voor de Wet van Newton toegepast op het masscentrum:
- Stelsel II
Deze 3 vergelijkingen vormen samen met het stelsel I de volledige beschrijving van de beweging en alle krachten die erbij optreden
Kinetische energie
De kinetische energie wordt hier uitgerekend ter controle van de alternatieve de aanpak in volgende paragraaf.
Alternatieve oplossing
[bewerken]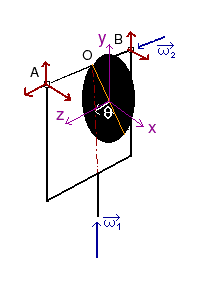
Een schijf is een rotatiesymmetrisch voorwerp. Bij de bovenstaande oplossing werd dit niet uitgespeeld. Als men deze eigenschap wel wil benutten, moet men een translerend assenkruis invoeren met oorsprong in het middelpunt van de schijf. "Translerend" betekent dus dat de x- en y-as horizontaal en vertikaal blijven. Men vindt nu voor de verschillende grootheden:
De rotatie van het asenkruis bestaat nu alleen uit ω1:
Dit is een bijzonder eenvoudige uitdrukking die weinig gelijkenissen vertoont met de vorige berekening. Om aan te tonen dat de beide voorstellingen wel equivalent zijn kan men ook hier de kinetische energie berekenen. Men moet nu wel rekenen volgens de formule van König (zie Massacentrum en energie). Deze formule kan hier geschreven worden als:
De snelheid van het massacentrum bestaat uit een sleepsnelheid en een relatieve snelheid. Deze laatste heeft nu 2 componenten:
Dit is een ontbinding in een orthogonaal assenkruis. Dus:
De traagheidsmomenten:
- Ixx = Iyy = mr2/4
- Izz = mr2/2
Hiermede wordt de kinetische energie:
... en dit is precies wat men hoger ook gevonden heeft.
Voor het berekenen van de momenten van de krachten worden eerst de coördinaten van de aangrijpingspunten bepaald:
- voor A (-rsinθ, rcosθ, AB/2)
- voor B (-rsinθ, rcosθ, -AB/2)
Het gewicht heeft nu als componenten: G(0,-mg,0). Hiermede bekomt men voor de momentenvergelijkingen het volgende stelsel:
De laatste vergelijking schijnt niet veel gelijkenissen te vertonen met de vorige z-component van de momentenvergelijking. Er zal verder nochtans aangetoond worden dat ze daarnaar kan herleid worden.
Om de vergelijkingen van de wet van Newton te kunnen opschrijven, moet men de versnelling projecteren in het huidige assenkruis:
Hiermede leidt de Wet van Newton tot het volgende stelsel:
Om de z-component van de momentenvergelijking te herleiden tot de uitdrukking van de vorige oplossing, wordt die herschreven als:
Hierin kan men nu gemakkelijk de uitdrukkingen voor XA+XB en YA+YB uit de vergelijkingen van Newton substitueren. Na een halve bladzijde rekenen zal men vaststellen dat men op de vorige uitdrukking voor de z-component uitkomt.
In deze benadering komt er nergens een hint dat een halve schijf een speciaal gedrag vertoont. Dat kan ook moeilijk want een halve schijf is geen rotatiesymmetrisch voorwerp en kan dus met deze aanpak niet behandeld worden.
Precessie bij een vrij bewegend voorwerp
[bewerken]Bij een vrij bewegend voorwerp, waarop alleen de zwaartekracht werkt en geen enkel uitwendig moment, moet het impulsmoment behouden blijven. Uit het voorgaande zou men de indruk kunnen krijgen dat dan alleen een rotatie rond een hoofdtraagheidsas mogelijk is. Het blijkt echter dat ook een combinatie van spin en precessie tot een constant impulsmoment kan leiden. Dit is bv. het geval bij een discus, die een waggelende beweging kan uitvoeren tijdens zijn vlucht.
Men onderstelt een rotatiesymmetrisch voorwerp dat draait rond zijn as met een ωs. Terzelfder tijd roteert het met een hoeksnelheid ωp onder een hoek θ. Beide bewegingen kunnen zich combineren tot een constant impulsmoment.

Als het impulsmoment een onveranderlijke richting moet hebben, dan kan dat alleen als het de richting heeft van ωp. Als het naast ωp zou vallen, dan zou het, in een vast referentiesysteem, een kegeloppervlak beschrijven rond ωp.
Er wordt een assenkruis verbonden aan het voorwerp ingevoerd met de y-as volgens ωs en met ωp en het impulsmoment in het yz-vlak. De x-as wijst naar de toeschouwer. Daar het om een rotatiesymmetrisch voorwerp gaat, is Ixx = Izz. Deze traagheidsmomenten zullen als Id (met de d van "dwars") aangeduid worden. Het traagheidsmoment volgens de symmetrieas zal Ia genoemd worden. Het impulsmoment L wordt:
Het is duidelijk dat ωx = 0 en ook Lx = 0 is. Daar er geen uitwendige momenten zijn, moet dit ook zo blijven. Dit betekent dat ook θ constant is en ωp en L steeds in het yz-vlak blijven.
Men schrijft nu de basiswet voor de rotatie verder uit. De uitwendige momenten en de relatieve verandering van L zijn 0. De hoeksnelheid van het assenkruis is enkel ωp. Er blijft dus:
Uitgewerkt in matrixvorm:
Hieruit blijkt dadelijk dat er enkel een x-component is:
Na invullen van de waarden voor de componenten van L en wat vereenvoudigen bekomt men:
Men werkt met een θ in het eerste kwadrant, dus een positieve cos θ. Men moet 2 gevallen onderscheiden:
1. Id > Ia : dan zijn ωp en ωs positief.
2. Id < Ia : dan zijn ωp en ωs tegengesteld gericht (hun scalair product is negatief).

Beide gevallen worden nu wat meer in detail besproken. Het eerste geval treedt op bij een eerder uitgerekt, langwerpig voorwerp. Dan is Id > Ia. De totale ogenblikkelijke rotatievector ωog beschrijft, in een vast referentiesysteem, een kegeloppervlak rond ωp met hoeksnelheid ωp. Wanneer een bewegende kegel over een stilstaande kegel rolt, dan ligt de ogenblikkelijk rotatievector op de raaklijn tussen de twee kegels. De situatie hier kan dus voorgesteld worden als het rollen van 2 kegels over elkaar. De kegel rond ωp noemt men de ruimtekegel en stelt de stilstaande kegel voor, de kegel rond ωs noemt men de voorwerpskegel. De voorwerpskegel heeft een halve tophoek die β genoemd wordt. Men kan L nu ook opschrijven als functie van ωog en die β:
Hiermede kan men een verband vinden tussen θ en β:
Als Id > Ia dan zal β kleiner zijn dan θ. Men krijgt een voorwerpskegel die uitwendig over de ruimtekegel rolt. Men noemt dit directe precessie.

Het tweede geval treedt op bij een voorwerp dat uitgebreider is in een richting loodrecht op de symmetrieas dan in de richting hiervan. Dit is bv. het geval bij een discus. In dat geval moeten ωp en ωs tegengestelde richtingen hebben. Of wiskundig correcter: hun scalair product moet negatief zijn. Zodra dat het geval is wordt de positie van de kegels omgewisseld. Men krijgt een ruimtekegel die aan de binnenzijde van de voorwerpskegel zit. Het blijkt dat ωp vrij groot moet zijn in vergelijking met ωs om aan de projecties van L in functie van ωog en β te kunnen voldoen. L en ωog moeten daarvoor in hetzelfde kwadrant vallen. Dat kan alleen als zowel ωp, ωog en L in hetzelfde kwadrant vallen. Klassiek verkiest men dan om ωs volgens de negatieve as te richten zodat zodat de drie andere vectoren positieve componenten hebben. Men krijgt dan de situatie zoals in de derde figuur. De voorwerpskegel rolt nu met zijn binnenzijde over de ruimtekegel. Volgens de hoger gegeven betrekking tussen θ en β moet β nu groter zijn dan θ, wat inderdaad klopt. Omdat ωs en ωp tegengestelde zin hebben, spreekt men van retrograde precessie.
In Dynamics van [meriam] kan men nog een studie vinden van de stabiliteit van dit soort beweging.
Aanvulling
[bewerken]De hoeken van Euler
[bewerken]De eerste studies van de algemene rotatie waren vooral gewijd aan het verklaren van de bewegingen van een tol. Euler leverde hierbij belangrijk werk door te bewijzen dat elke willekeurige rotatie kan geschreven worden als de som van drie rotaties die door één punt passeren. Deze worden gedefinieerd via de hoeken van Euler. Spijtig genoeg zijn de benamingen en de definities van deze niet uniform bij de verschillende auteurs. Daarom moet men steeds goed uitkijken welke definitie in een bepaald werk gevolgd wordt. Voor een uitvoerige bespreking kan men opnieuw terecht bij https://mathworld.wolfram.com/EulerAngles.html . De methode die hier hierboven gevolgd werd voor het analyseren van de willekeurige rotatie en die steunt op matrixrekenen, is recenter en biedt een veel grotere vrijheid bij het behandelen van een probleem.

Bij de rotatie van een star lichaam werkt men met een assenkruis dat vast verbonden is aan het voorwerp. Als dit voorwerp een vast punt heeft maar voor de rest voortdurend van oriëntatie verandert, zoals meestal het geval is bij een tol, dan bieden de hoeken van Euler een mogelijkheid om de positie van het referentiesysteem eenduidig te bepalen. Men vertrekt daarbij van een klassiek rechtsdraaiend cartesisch assenkruis (x,y,z). Van hieruit gaat men over naar een tweede assenkruis door een rotatie over een hoek φ rond de z-as. Dit levert het assen kruis (x',y',z). Door een rotatie rond de x'-as over een hoek θ gaat men over naar het assenkruis (x',y",z"). Door een rotatie over een hoek ψ rond de z"-as gaat men uiteindelijk over naar het actuele assenkruis (X,Y,Z).
Wanneer deze drie hoeken veranderen in de tijd, krijgt men de rotatie van het voorwerp beschreven als de som van deze drie rotaties. Men moet in de praktijk de projecties ervan in het laatste assenkruis hebben. Deze projecties zijn gemakkelijk te volgen op de figuur. Het meest ingewikkelde geval is de projectie van , de rotatie rond de oorspronkelijke z-as. Het is duidelijk dat de projectie op de Z-as gegeven is door te vermenigvuldigen met cos θ. De projectie aan de andere zijde van de oorspronkelijke z-as, door te vermenigvuldigen met sin θ, valt op de y"-as en moet dan nogmaals geprojecteerd worden op de X-as en Y-as. Projectie op deze assen vraagt een vermenigvuldigen met resp. sin ψ en cos ψ. Men krijgt dus:
Alles samen krijgt men in het nieuwe assenkruis:
De verschillende snelheden hebben een fysische betekenis bij de beweging van een tol of een hemellichaam, zoals bv. onze aarde. De rotatie rond de Z-as is bij de aarde verantwoordelijk voor dag en nacht. Bij een rotatiesymmetrisch voorwerp noemt men dit de spin of spilomwenteling. Wanneer de Z-as helt t.o.v. de oorspronkelijke z-as en er is alleen een , dan beschrijft de top van de Z-as een cirkel rond de z-as. Dit noemt men de precessie. Een verandering van de hoek θ zorgt voor een nutatie (= knikken). Deze beweging treedt normaal zeer sterk op wanneer een tol zijn snelheid verliest. Meestal is er eerst een zuivere precessie, waarbij de eigen as van de tol rond een verticale draait. Hierbij beschrijft de top van de Z-as een cirkel rond de z-as. Daarna begint de hoek met deze verticale regelmatig groter en kleiner te worden, met een steeds grotere amplitude. Dit is de nutatie. Dan beschrijft de top van de Z-as een golvende lijn ronde z-as.
Gyratiestraal - Traagheidsellipsoïde
[bewerken]Soms wordt een traagheidsmomenten ook gespecificeerd m.b.v. een gyratiestraal. De gyratiestraal is de straal van de cirkel waarop alle massa zich zou moeten bevinden om het gegeven traagheidsmoment t.o.v. een as te hebben. Als de totale massa van een voorwerp m is, het traagheidsmoment volgens een bepaalde as I, dan is de gyratiestraal R bepaald door:
- mR2 = I
De traagheidstensor I kan gevisualiseerd worden als een ellipsoïde. Een omwentelingsellipsoïde is het lichaam dat ontstaat als men een ellips rond een hoofdas laat wentelen. Daarbij is de doorsnede loodrecht op die as een cirkel. Als dit ook een ellips is heeft men een gewone ellipsoïde.

De standaardvorm van de vergelijking is:
waarbij a, b en c de helft is van de lengte van de as voglens x, yen z. In de figuur is dit 4, 2 en 1.
De traagheidstensor I kan nu gevisualiseerd worden als een ellipsoïde met de vergelijking:
Als de 3 diagonaalelementen van de matrix I positief zijn heeft men een ellipsoïde die gecentreerd is rond de oorsprong van het assenkruis. Dit is hier duidelijk het geval. Deze ellipsoïde heeft de eigenschap dat de symmetrieassen van de ellipsoïde samenvallen met de hoofdtraagheidsassen. Verder blijkt dat het kwadraat van de afstand van het centrum C tot een punt P op het oppervlak omgekeerd evenredig is met het traagheidsmoment volgens de richting van CP. Om dit aan te tonen wordt gesteund op het feit dat de traagheidstensor het traagheidsmoment volgens een bepaalde as door de oorsprong levert als men eenheidsvector volgens die as gebruikt voor de volgende bewerking (bewijs infra traagheidsmoment volgens willekeurige richting):
De positievector CP van C naar P kan dan geschreven worden als het product van de lengte CP met een eenheidsvector volgens CP:
Vult men deze vector in in de vergelijking van de ellipsoïde dan krijgt men:
Bemerk dus wel dat het grootste traagheidsmoment overeenkomt met de kleinste as van de ellipsoïde. Ook zal de ellipsoïde van vorm veranderen zodra men een ander punt van het voorwerp als oorsprong neemt.
Meestal definieert men deze traagheidsellipsoïde door te vertrekken van deze eigenschap, nl. door ze te definiëren als een oppervlak zodat de afstand van het middelpunt tot een punt op het oppervlak omgekeerd evenredig is met het de vierkantswortel uit het traagheidsmoment volgens die richting.
Transformaties van de traagheidstensor en de traagheidsellipsoïde
[bewerken]In dit deel zal getoond worden hoe de elementen van de traagheidstensor veranderen bij rotatie van het assenkruis. Hiervoor wordt beroep gedaan op het voorwerp weergegeven in de figuur. Dit voorwerp is gevormd door 4 bollen, die als puntmassa's zullen beschouwd worden. De bollen m1 en de m2 liggen in een verticaal vlak, de twee andere in een horizontaal vlak. Alle bollen hebben een massa van 2 kg. Eerst zal de traagheidstensor rechtsreeks berekend worden in het xyz-assenkruis, dat een hoofdtraagheidsassenkruis is. Daarna zal deze berekend worden in een assenkruis x'y'z, dat over 30° naar rechts gedraaid is t.o.v. het vorige. Tenslotte zullen de formules afgeleid worden die tonen hoe de elementen van de traagheidstensor veranderen bij een rotatie van het assenkruis en zal dit toegepast worden op het voorbeeld.
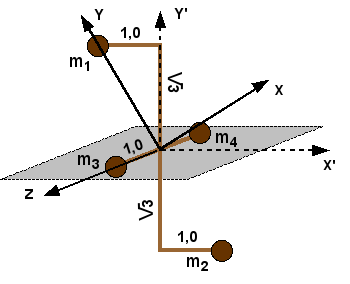
Rechtstreekse berekening van de traagheidstensor
[bewerken]In eerste assenkruis
[bewerken]De coördinaten van de 4 bollen kunnen gemakkelijk afgelezen worden van de figuur.
Hiermede kunnen de elementen van de traagheidstensor uitgerekend worden:
- = 20 kgm2
- = 4 kgm2
- = 16 kgm2
De traagheidsproducten moeten nul zijn:
Dit leidt tot een diagonale traagheidstensor van de vorm:
In tweede assenkruis
[bewerken]De coördinaten van de 4 bollen worden weer afgelezen worden van de figuur.
De diagonaalelementen van de traagheidstensor worden:
- = 16 kgm2
- = 8 kgm2
- = 16 kgm2
De traagheidsproducten worden nu:
- kgm2
Dit leidt tot een traagheidstensor van de vorm:
Invarianten
[bewerken]De traagheidstensor heeft een paar invarianten onder de rotatie van het assenkruis.
1. Het spoor van de matrix, d.i. de som van de elementen op de hoofdiagonaal. Bij de eerste matrix is dit 20+4+16 = 40. Bij de tweede matrix is dit 16+8+16 = 40.
2. De determinantwaarde van de matrices. Bij de eerste is dit gewoon het product van de elementen op de hoofddiagonaal: 20*4*16 = 1280. Bij de tweede is dit
De transformatie van de traagheidstensor
[bewerken]De enige transformatie hier zal beschouwd worden is een rotatie van het assenkruis. In het voorbeeld moeten ook alleen de xy-assen geroteerd worden, zodat alleen een rotatie in het vlak zal behandeld worden.
Een transformatie kan altijd op twee manieren bekeken worden: als een transformatie van het assenkruis of als een transformatie van een figuur. Bij een fysisch probleem, waarbij het voorwerp een bepaalde oriëntatie heeft, bv. t.o.v. de gewichtsvector, zal men een transformatie eerder zien als een verandering van het assenkruis. Bij een tekenprogramma echter werkt men meestal binnen een vast assenkruis verbonden aan het tekenblad en werkt men met transformaties die de figuren veranderen of verplaatsen. Een transformatie die een rotatie van een assenkruis naar rechts voorstelt, zal bij een tekenprogramma resulteren in een rotatie naar links van de figuur. Het is dus belangrijk dat men steeds hetzelfde standpunt blijft innemen bij het bespreken van transformaties. Hier wordt er gesproken over een transformatie van het assenkruis.
Er zal ook regelmatig gesproken worden van het "oude" assenkruis (xy-assen) en het "nieuwe" assenkruis (x'y'-assen). Een rotatie van het assenkruis kan voorgesteld worden door een vierkante matrix, in dit geval 2x2. De elementen ervan kunnen op eenvoudige wijze bepaald worden door de basisvectoren van het nieuwe assenkruis te projecteren in het oude. Bemerk echter dat de rotatie van het oude assenkruis naar het nieuwe hier een rotatie over -30° is. Dat minteken is reeds verrekend bij het opschrijven van de projecties hieronder. Voor de z-component verandert er niets in het voorbeeld.

Men vindt:
De matrix voor de transformatie van oud naar nieuw assenkruis wordt gevormd door deze geprojecteerde basisvectoren te gebruiken als rijen:
R(-30°) =
Men kan gemakkelijk controleren dat het product van één van de geprojecteerde basisvectoren met deze matrix leidt tot een basisvector in het nieuwe assenkruis. Bij vermenigvuldigen van een rij van de matrix met een geprojecteerde eenheidsvector als kolomvector komt overeen met een scalair product van die vector met zichzelf, wat als resultaat 1 levert, of met een andere geprojecteerde basisvector. Daar de basisvectoren loodrecht op elkaar staan is het resultaat dan 0. Men kan ook gemakkelijk controleren dat deze transformatie toegepast op de posities van m1 en m2 in het oude assenkruis de posities in het nieuwe leveren.
Bemerk dat bij de inverse rotatie, over +30°, alleen de elementen van de nevendiagonaal, de sin θ, van teken wisselen.
Elk element van de traagheidstensor is de som van producten van 2 coördinaten. Er is echter geen mogelijkheid om de traagheidstensor in zijn geheel te schrijven in termen van matrixproducten. Men moet daarom beroep doen op de formulering van een algemene term van de nieuwe traagheidstensor. Een algemene formule voor een nieuwe coördinaat na transformatie van een vector a is:
Voor het product van 2 coördinaten krijgt men:
Dit levert in driedimensionaal systeem 9 termen die elke bestaan uit het product van 4 getallen. Daar een product commutatief is, heeft het geen belang in welke volgorde men die getallen opschrijft. Het heeft trouwens ook geen belang in welke volgorde men de sommaties uitvoert. het resultaat zal steeds dezelfde producten van 4 getallen opleveren. Men kan daarom kortweg opschrijven:
Dit is ook de transformatieformule voor de elementen van de traagheidstensor:
- ( I )
Dit kan nu toegepast worden voor het transformeren van de eerste traagheidstensor in de tweede. Gelukkig zijn vele elementen van de eerste matrix 0 en ook een deel elementen van R. Het eerste element van de nieuwe tensor wordt uitgerekend met de formule:
Daar zeer veel termen 0 zijn, blijft uiteindelijk over:
- kgm2
Op analoge manier vindt men:
- kgm2
- kgm2
De overige termen blijven ongewijzigd.
Bij de bespreking van de traagheidsellipsoïde zal blijken dat er voor de traagheidstensor toch wel een manier is om deze transformatie op een eenvoudiger manier in termen van matrixvermenigvuldigingen te schrijven.
Het diagonaliseren van de traagheidstensor
[bewerken]Er werd hoger gesteld dat men de traagheidstensor altijd kan omvormen tot een diagonale matrix door een geschikte keuze van het assenkruis.Er zal nu geprobeerd worden om de tweede matrix te diagonaliseren en zo, hopelijk, de eerste terug te vinden. Dat zal echter maar gedeeltelijk lukken. Daar alleen de x- en y-coördinaten bij de transformatie betrokken zijn, zal alles behandeld worden als een tweedimensionaal probleem.
Het diagonaliseren van een matrix berust op het zoeken van de eigenvectoren. Eigenvectoren van een matrix zijn vectoren die door die matrix niet van richting veranderd worden, alleen van grootte. Formeel opgeschreven: is een eigenvector van de matrix R als . De coëfficiënt λ wordt de eigenwaarde van de vector genoemd. Men krijgt:
Voor een oplossing verschillend van de nulvector moet de determinant van het stelsel = 0 zijn. Dit levert een kwadratische vergelijking in λ en zal dus 2 oplossingen voor λ leveren. Dat de determinant van het stelsel 0 is, betekent echter ook dat er een onbepaaldheid zal zitten op de eigenvector. Het is echter duidelijk dat als een eigenvector is, ook elke vector van de vorm een oplossing zal zijn en dus ook een eigenvector. Voor het voorbeeld krijgt men:
of
De oplossingen zijn λ1 = 4 en λ2 = 20 (wat verwacht werd). Hier duikt nu een eerste probleem op als men wil terugkeren naar de oorspronkelijke matrix. Men heeft geen enkele aanduiding welke eigenwaarde bij de basisvector volgens de nieuwe x-as hoort en welke bij de nieuwe y-as. Men kan en moet er alleen voor zorgen dat men een rechtsdraaiend assenkruis behoudt. Deze eis wordt wiskundig vertaald naar een transformatiematrix met determinantwaarde = +1.
De eerste eigenvector haalt men uit het stelsel dat men bekomt door λ1 te substitueren in het stelsel dat de eigenvectoren definieert:
Men ziet dat beide rijen afhankelijk zijn, wat een uitdrukking is van de verwachte onbepaaldheid. Men moet voor één coördinaat zelf een waarde kiezen, daarna volgt een waarde voor de andere coördinaat uit om het even welke van beide vergelijkingen. Kiest men e1=1 dan volgt ey =-31/2. Om deze vector als basisvector te kunnen gebruiken wordt hij genormeerd:
Hiermede wordt e1x = 1/2 en e1y = -31/2/2
Op analoge manier vindt men voor de tweede eigenvector dat e2y = 1/31/2 Na normeren krijgt men:
Men kan gemakkelijk controleren dat beide vectoren loodrecht op elkaar staan.

Hiermede kan een transformatiematrix R geconstrueerd worden:
De determinantwaarde is +1. Als men e1 gebruikt voor de x-as en e2 voor de y-as en de huidige z-as behoudt, dan heeft men een rechtsdraaiend assenkruis. Om naar de originele matrix terug te keren moet men een rotatie over +30° uitvoeren. Het element R12 is sin θ. Het blijkt dat de matrix een rotatie over -60° voorstelt. De x-as zal dus samenvallen met de vroegere -y-as en de y-as met de x-as!
Als men de volgorde van de eigenvectoren omwisselt, bekomt men als transformatiematrix
De determinantwaarde hiervan blijkt -1 te zijn. Dat betekent dat men de richting van één van de vectoren moet omklappen. Een rotatiematrix voor een hoek < 90° heeft normaal positieve elementen op de hoofddiagonaal. Het is dus aangewezen om de onderste vector met -1 te vermenigvuldigen. Dan komt men wel terug op het eerste assenkruis.
Men kan nu deze rotatiematrix gebruiken om opnieuw de tweede tensor om te rekenen naar de eerste. Hierbij zullen de eerste 2 diagonaalelementen wel omgewisseld worden. Men bekomt:
Op analoge manier bekomt men: en
Het kan gebeuren dat 2 eigenwaarden gelijk zijn. Dan is er een bijkomende onbepaaldheid en moet men 2 coördinaten vrij kiezen. Dit zal bv. gebeuren bij een omwentelingsellipsoïde. Een doorsnede loodrecht op de omwentelingsas is dan een cirkel en een cirkel heeft geen voorkeursrichtingen. Elk paar orthogonale vectoren in dat vlak kan als basis dienen.
De traagheidsellipsoïde
[bewerken]Hoger werd reeds gesteld dat men de traagheidstensor kan visualiseren als een ellipsoïde door hem te gebruiken in de vergelijking:
Bij de notatie van vectoren als kolommatrices, moet een scalair product uitgewerkt worden als het matrixproduct van de transpose van de eerste vector met de tweede. De transpose van een matrix is een matrix met de rijen en kolommen omgewisseld. Voor een matrixproduct is er geen specifieke operator. De twee matrices worden naast elkaar geschreven, zoals men ook ab schrijft voor a x b. Men heeft dus voor een scalairproduct:
Met deze wetenschap kan men de bovenstaande formule ook schrijven als een scalair product:
Voor de transformatie van een operator naar een ander assenkruis kan men volgende analogie gebruiken. Als men in open veld in een rechte lijn van A naar B wandelt en men komt een rivier tegen waarop geen brug ligt volgens de lijn AB maar wel iets verder, dan wandelt men langs de rivier naar de brug, steekt daar de rivier over en loopt dan aan de overkant terug naar de lijn AB. Voor de toepassing hier: als men de traagheidstensor heeft in functie van de oude coördinaten, dan transformeert men de nieuwe terug naar de oude, past de operator toe en transformeert het resultaat terug naar de nieuwe coördinaten.
Als R de transformatie voorstelt van de oude naar de nieuwe coördinaten, van , dan moet men de inverse gebruiken om de nieuwe coördinaten terug om te zetten naar de oude. Men krijgt in het nieuwe assenkruis:
Bij een rotatiematrix is de transpose hetzelfde als de inverse matrix. Men krijgt dus links bij het uitwerken
.
In termen van matrixproducten krijgt men dus:
Of voor de nieuwe tensor:
- (II)
Men moet bedenken dat de reeks matrices van rechts naar links zullen worden toegepast bij een vermenigvuldiging met een kolommatrix.
Toegepast op de transformatie van de eerste tensor naar de tweede (om de berekeningen eenvoudig te houden alleen de xy-componenten) krijgt men:
Men kan aantonen dat in dit speciale geval beide transformaties, (I) en (II) hetzelfde zijn. Als A en B vierkante matrices zijn, dan wordt een element van het product AB gevormd door elk element van een rij van A te vermenigvuldigen met het overeenkomstig element van een kolom van B. Of:
Bij A loopt de index dus over de kolommen, bij B over de rijen. In de formule (I) voor de transformatie van I, hieronder hernomen, blijkt de index telkens over de kolommen van transformatiematrix te lopen. Men kan dit veranderen door een matrix te vervangen door zijn transpose:
Daar bij een rotatiematrix de transpose ook de inverse is, is de transformatie van de traagheidstensor in (I) in dit speciale geval gelijk aan de matrixvermenigvuldiging in (II)
Traagheidsmoment volgens een willekeurige richting
[bewerken]In een vorige paragraaf werd gesteld dat men het traagheidsmoment volgens een willekeurige as met richting door het centrum van traagheidsellipsoïde kan vinden met de bewerking:
- (III)

Om dit te bewijzen moet men eerst het traagheidsmoment van een puntmassa mi met positievector t.o.v. deze as bepalen. Dit traagheidsmoment is mi.d2 waarin d de loodrechte afstand is van de puntmassa naar de as.
Uit de figuur blijkt dat d een rechthoekszijde is van een rechthoekige driehoek. De andere rechthoekszijde wordt gevormd door de projectie van op de as. Dit kan uitgewerkt worden door een scalair product van met . Om met numerieke indices te kunnen werken zullen de componenten van aangeduid worden als ri,j, met j=1,2,3 voor de coördinaten x,y,z. Men krijgt dus:
Er is nu nog nood aan een algemene vorm voor een element van de traagheidstensor. Dit kan m.b.v. de Kroneckerdelta. Dit is een functie die de waarde 0 of 1 kan aannemen volgens de volgende conventie:
Hiermede kan men schrijven [1]:
of, voor een continue massaverdeling: (met r1 = x, r2 = y, r3 = z)
Men kan dit controleren door de uitdrukking uit te schrijven voor een paar termen:
Men ziet reeds duidelijk het patroon dat optreedt en inderdaad leidt tot de traagheidstensor.
Als men hiermede de uitdrukking (III) wil uitwerken, dan moet men schrijven:
Als men dit uitwerkt voor één massa bekomt men:
Hierbij leveren de termen in rk2 leveren uiteindelijk De overige, negatieve, termen leveren duidelijk het kwadraat van het scalair product, zodat men dus inderdaad heeft:
Wat moest bewezen worden.
Er werd hier bijna overal een matrixformulering gebruikt. Historisch gezien werd eerder met functies gewerkt. Voor het traagheidsmoment volgens een willekeurige richting werd de eenheidsvector eerst geschreven in functie van de cosinussen van de hoeken met de assen:
Hiermede kan men de d2 uit de figuur opschrijven als
Als men de eerste term vermenigvuldigt met 1, maar onder de vorm van , alles met mi vermenigvuldigt en sommeert over alle massa's, dan bekomt men het traagheidsmoment volgens de gegeven richting als een homogene kwadratische functie van de cosinussen van de hoeken:
Van hier was het een kleine stap naar de traagheidsellipsoïde. Ook de kinetische energie werd met deze functie berekend, met de componenten van de ogenblikkelijke rotatievector i.p.v. de cosinussen. De componenten van de ogenblikkelijke rotatievector ω kan men schrijven als:
Hiermede wordt Het is immers een homogene kwadratische functie. Dus:
Met deze uitdrukking voor de kinetische energie kon men dan aan de slag om de bewegingsvergelijkingen op te stellen met de methode van Lagrange (volgend hoofdstuk).
Toepassing
Men kan dit ter controle even toepassen. In het eerste assenkruis wordt de richting van de x-as gekozen: (1; 0; 0). Het is vrij duidelijk dat dit een I = 20 oplevert. In het tweede assenkruis wordt dit de richting
- (of: een eenheidsvector in de richting +30°)
Hiermede krijgt men:
Q.E.D.
Nota
- ↑ met dank aan Christian Gruber en Willy Benoit. Zie [gruber] in de Bibliografie
Alles wat in dit laatste deel staat over de transformatie van de traagheidstensor en de traagheidsellipsoïde, is terug te vinden in [goldstein] (zie in de Bibliografie) en ook in [gruber], maar wat meer wiskundig en zonder de uitgewerkte voorbeelden. De aandacht voor de alternatieve manier om het impulsmoment te berekenen berust op [gruber] en op eigen ervaring.


















![{\displaystyle {\vec {L}}=\left[{\begin{matrix}\ I_{xx}&-I_{xy}&-I_{xz}\\-I_{yx}&\ I_{yy}&-I_{yz}\\-I_{zx}&-I_{zy}&\ I_{zz}\\\end{matrix}}\right]\left[{\begin{matrix}\omega _{x}\\\omega _{y}\\\omega _{z}\\\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59f04e8f63c4cd55ec162b6823b4d1064b66b27d)



![{\displaystyle L_{x}=\sum _{i}m_{i}[y_{i}(\omega _{x}y_{i}-\omega _{y}x_{i})-z_{i}(\omega _{z}x_{i}-\omega _{x}z_{i})]=\sum _{i}m_{i}(y_{i}^{2}\omega _{x}-x_{i}y_{i}\omega _{y}-x_{i}z_{i}\omega _{z}+z_{i}^{2}\omega _{x})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4b95af60ca5d161cc27ea81fb89248947cb9a41)
![{\displaystyle =\sum _{i}m_{i}[(y_{i}^{2}+z_{i}^{2})\omega _{x}-x_{i}y_{i}\omega _{y}-x_{i}z_{i}\omega _{z}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c87a666a08ce23335e983bb13dadee46a2e7b073)
![{\displaystyle L_{y}=\sum _{i}m_{i}[-x_{i}y_{i}\omega _{x}+(x_{i}^{2}+z_{i}^{2})\omega _{y}-x_{i}z_{i}\omega _{z}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08de77b3b27ec13e3474e1bfcfd14fcd574f5ba2)
![{\displaystyle L_{z}=\sum _{i}m_{i}[-x_{i}z_{i}\omega _{x}-y_{i}z_{i}\omega _{y}+(x_{i}^{2}+y_{i}^{2})\omega _{z}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/344d1cb6e689c4ca89380be34f882540875369fe)




![{\displaystyle {\vec {L}}=\left[{\begin{matrix}I_{xx}&0&0\\0&I_{yy}&0\\0&0&I_{zz}\\\end{matrix}}\right]\left[{\begin{matrix}\omega _{x}\\\omega _{y}\\\omega _{z}\\\end{matrix}}\right]=\left[{\begin{matrix}I_{xx}\omega _{x}\\I_{yy}\omega _{y}\\I_{zz}\omega _{z}\\\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dbfe9ddd240a4fb76862c8c7849c8aea6074cf61)









![{\displaystyle {\vec {L}}=\left[{\begin{matrix}{I_{xx}}&0&0\\0&I_{yy}&{-{\frac {mhb}{4}}}\\0&{-{\frac {mhb}{4}}}&I_{zz}\\\end{matrix}}\right]\left[{\begin{matrix}0\\0\\{\omega }\\\end{matrix}}\right]=\left[{\begin{matrix}0\\{-{\frac {mhb\omega }{4}}}\\{m\omega ({\frac {b^{2}}{3}}+{\frac {d^{2}}{12}})}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c97853e59f10f3377ccf5d3bca21d1ab31e8b730)



![{\displaystyle {\vec {L}}={\vec {L}}_{C}\;+\;{\vec {r}}_{C}\,\times \,m{\vec {v}}_{C}=I_{zz}\omega {\vec {k}}\;+\;\left[{\begin{matrix}{\vec {i}}&{\vec {j}}&{\vec {k}}\\{0}&{\frac {b}{2}}&{\frac {h}{2}}\\{-m{\frac {b}{2}}\omega }&{0}&{0}\\\end{matrix}}\right]={\frac {m}{12}}(b^{2}+d^{2})\omega {\vec {k}}\;-{\frac {mhb\omega }{4}}{\vec {j}}+{\frac {mb^{2}}{4}}\omega {\vec {k}}=-{\frac {mhb\omega }{4}}{\vec {j}}\;+\;m\omega \left({\frac {b^{2}}{3}}+{\frac {d^{2}}{12}}\right){\vec {k}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d62ddf350e3dd805af5181a396f1ad39099774ae)





![{\displaystyle {\vec {\omega }}_{assenkruis}\times {\vec {L}}=\left[{\begin{matrix}{\vec {i}}&{\vec {j}}&{\vec {k}}\\{\omega _{x}}&{\omega _{y}}&0\\L_{x}&L_{y}&0\\\end{matrix}}\right]=(I_{yy}-I_{xx})\omega _{x}\omega _{y}\,{\vec {k}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b1c9024ea95ed66eb7c3fd8b42445788d29184f6)

![{\displaystyle \left[{\begin{matrix}{\vec {i}}&{\vec {j}}&{\vec {k}}\\0&0&-\omega _{2}\\0&L_{y}&L_{z}\\\end{matrix}}\right]=\omega _{2}.L_{y}\,{\vec {i}}=I_{yy}\omega _{1}\omega _{2}\,{\vec {i}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44f84a9829f120a38ba07012687602c37b6fd235)
![{\displaystyle E_{kin}=({\vec {\omega }}\cdot {\vec {L}})/2={\frac {1}{2}}\left[{\begin{matrix}\omega _{x}&\omega _{y}&\omega _{z}\\\end{matrix}}\right]\left[{\begin{matrix}L_{x}\\L_{y}\\L_{z}\\\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4fcc0730246c8ca0952d91c61c54c33f40a90322)





![{\displaystyle E_{kin}={\frac {1}{2}}[0\ 0\ \omega ]\left[{\begin{matrix}0\\{-{\frac {mhb\omega }{4}}}\\{m\omega ({\frac {b^{2}}{3}}+{\frac {d^{2}}{12}})}\end{matrix}}\right]=m\omega ^{2}\left({\frac {b^{2}}{6}}+{\frac {d^{2}}{24}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e15cd235c977b7607d4fe216100506cbd5fde17)









![{\displaystyle =[(I_{zz}-I_{yy})\sin \theta .\omega _{1}.{\dot {\theta }}]{\vec {i}}+[(I_{zz}-I_{xx})\cos \theta .\omega _{1}.{\dot {\theta }}]{\vec {j}}+[(I_{xx}-I_{yy})\sin \theta .\cos \theta .\omega _{1}^{2}]{\vec {k}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/916d91af377c929f3929a7f6c2462c22ddfaf94e)












































![{\displaystyle \left[{\begin{matrix}{\vec {i}}&{\vec {j}}&{\vec {k}}\\0&\omega _{p}\cos \theta &\omega _{p}\sin \theta \\0&L_{y}&L_{z}\end{matrix}}\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9883f43d274e3bfdcb677b9f93006474bc1934f9)









![{\displaystyle [x\ y\ z][\mathrm {I} (3x3)]\left[{\begin{matrix}x\\y\\z\end{matrix}}\right]=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/129632652a16af3eb39fbedfdfa975bb7dea3c1e)

![{\displaystyle I_{u}=[u_{x}\ u_{y}\ u_{z}][\mathrm {I} (3x3)]\left[{\begin{matrix}u_{x}\\u_{y}\\u_{z}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7841269366a11bf22cdb1b26f9ad9a3c3e31175a)












![{\displaystyle I=\left[{\begin{matrix}20\,&\,0\,&\,0\,\\0&4&0\\0&0&16\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/11ab22351d0c608dbd2ebd596dd80d407689fbec)




![{\displaystyle I_{zz}=\sum m_{i}(x_{i}^{2}+y_{i}^{2})=m[(1+3)+(1+3)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d050b17fe534dd41d74b4f55fc8c1fee1a289e2e)

![{\displaystyle I=\left[{\begin{matrix}16\,&\,4{\sqrt {3}}\,&\,0\,\\4{\sqrt {3}}&8&0\\0&0&16\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b4697c8d2d08193ad54a975d3783b83b2fdc5a6)



![{\displaystyle \left[{\begin{matrix}{\sqrt {3}}/2&-0,5&0\\0,5&\,{\sqrt {3}}/2&0\\0&0&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac38485759ccde2b5cdc0fc4f5935a058d5a4da6)















































![{\displaystyle I_{as}=\sum _{ij}I_{ij}u_{i}u_{j}=\sum _{ij}\left[\sum _{k}m_{k}(r_{k}^{2}\delta _{ij}-r_{k,i}r_{k,j})\right]u_{i}u_{j}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43f6f1290f65fd519d879bc8c2cdfcfcd14e71a0)
![{\displaystyle {\begin{matrix}m_{k}[r_{k}^{2}u_{1}^{2}-r_{k,1}^{2}u_{1}^{2}-r_{k,1}r_{k,2}u_{1}u_{2}-r_{k,1}r_{k,3}u_{1}u_{3}\\-r_{k,2}r_{k,1}u_{2}u_{1}+r_{k}^{2}u_{2}^{2}-r_{k,2}^{2}u_{2}^{2}-r_{k,1}r_{k,3}u_{1}u_{3}\\-r_{k,3}r_{k,1}u_{3}u_{1}-\ldots ]\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13d499e71ebe2e08e67d1f4b24465fb1fc903160)

![{\displaystyle I_{as}=\sum _{k}m_{k}[r_{k}^{2}-({\vec {r}}_{k}\cdot {\vec {u}})^{2}]={\vec {u}}\cdot I\,{\vec {u}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0580bdeda1304c85c8a081e0eb7375499507e19)








