Klassieke Mechanica/Centrale kracht

Centrale kracht en planetenbanen

Het tweelichamenprobleem

De aarde draait rond de zon, de maan draait rond de aarde. Dit gebeurt onder invloed van de aantrekkingskracht tussen deze hemellichamen. In het geval van de aarde en de maan kan men zich toch wel afvragen of de aantrekkingskracht van de maan de aarde niet van haar baan om de zon doet afwijken. Dit blijkt inderdaad het geval. De analyse van dit soort situaties staat in de mechanica bekend als "het tweelichamenprobleem".

twee lichamen probleem

In feite draaien aarde en maan rond hun gemeenschappelijk massacentrum en draait dit massacentrum rond de zon. Als men even de aantrekkingskracht van de zon buiten beschouwing laat, dan heeft men 2 voorwerpen die mekaar aantrekken. Men kan hun positie t.o.v. een willekeurige oorsprong beschrijven m.b.v. de twee positievectoren r₁ en r₂ en . Men kan ze echter ook beschrijven m.b.v. de positievector r_C van het massacentrum en twee relatieve positievectoren r'₁ en r'₂. Als beide de massa's van die voorwerpen gegeven worden door m₁ en m₂, dan wordt de positie van het massacentrum gegeven door

${\vec {r}}_{C}={\frac {m_{1}{\vec {r}}_{1}+m_{2}{\vec {r}}_{2}}{m_{1}+m_{2}}}$

De relatieve positievectoren worden dan gegeven door (volgens het recept: relatieve positie = eindpunt - beginpunt):

${\vec {r}}'_{1}={\vec {r}}_{1}-{\vec {r}}_{C}={\frac {m_{2}({\vec {r}}_{1}-{\vec {r}}_{2})}{m_{1}+m_{2}}}$

Als men nu een positievector van het tweede voorwerp t.o.v. het eerste invoert

$\displaystyle {\vec {r}}={\vec {r}}_{2}-{\vec {r}}_{1}$

dan wordt dit:

${\vec {r}}'_{1}=-{\frac {m_{2}{\vec {r}}}{m_{1}+m_{2}}}$

Op analoge manier vindt men dat:

${\vec {r}}'_{2}=-{\frac {m_{1}{\vec {r}}}{m_{1}+m_{2}}}$

De kinetische energie van dit systeem kan m.b.v. de formule van König opgeschreven worden als:

$E_{k}={\frac {1}{2}}(m_{1}+m_{2}){\vec {r}}_{C}^{2}+{\frac {1}{2}}(m_{1}{\vec {r'}}_{1}^{2}+m_{2}{\vec {r'}}_{2}^{2})={\frac {1}{2}}(m_{1}+m_{2}){\vec {r}}_{C}^{2}+{\frac {1}{2}}{\frac {m_{1}m_{2}}{m_{1}+m_{2}}}{\vec {r}}^{2}$

De eerste term is de kinetische energie van translatie van het massacentrum. De tweede term kan gelezen worden als de kinetische energie van een voorwerp met massa m₁m₂/(m₁ + m₂) op een afstand r van het eerste voorwerp. M.a.w. als men de beweging van de maan rond de aarde wil beschrijven alsof de aarde stilstaat, dan kan dat op voorwaarde dat men aan de maan een andere massa toekent. Die massa noemt men de gereduceerde massa en is gegeven door:

$\mu ={\frac {m_{1}m_{2}}{m_{1}+m_{2}}}$

Soms wordt dit ook geschreven als

${\frac {1}{\mu }}={\frac {1}{m_{1}}}+{\frac {1}{m_{2}}}$

Hetzelfde geldt voor de baan van een satelliet rond de aarde of de aarde rond de zon. In beide gevallen echter is de massa van het tweede voorwerp zeer klein t.o.v. de massa van het eerste voorwerp. Men kan de eerste definitie van μ in teller en noemer delen door m₁:

$\mu ={\frac {m_{2}}{1+m_{2}/m_{1}}}$

Als m₁ veel groter is dan m₂, dan blijft de noemer ongeveer 1 en is de massa μ dus zeer dicht bij de werkelijke massa m₂ van de planeet of satelliet.

Het feit dat de aarde en de maan rond hun gemeenschappelijk massacentrum draaien, verklaart een deel van de getijden. Het massacentrum van het systeem aarde-maan valt binnen de aarde. Er is een hoogtij aan de kant van de maan, veroorzaakt door de aantrekkingskracht van de maan. er is echter ook een hoogtij aan de tegenovergestelde zijde van de aarde, omdat dat punt het verst ligt van dat massacentrum en daardoor een grotere middelpuntvliedende kracht ondervindt (zie hiervoor eventueel het hoofdstuk over traagheidskrachten). Beide effecten blijken in grootte dicht bij elkaar te liggen.

Centrale kracht

Potentiaalfunctie

Wanneer men een krachtveld heeft waarin alle dragers van de krachten door één bepaald punt passeren en de grootte alleen afhankelijk is van de afstand tussen de twee voorwerpen, dan spreekt men van een centrale kracht. Er kan aangetoond worden dat de gravitatiekracht die uitgaat van een bol, een resultante heeft die aangrijpt in het centrum van de bol (door integreren over de bol). De aantrekkingskracht van de zon en de planeten is dus een centrale kracht, die kan beschowud worden als wijzend naar het centrum van de zon of de planeet.

gesloten kromme in centraal krachtveld

Een centrale kracht heeft altijd een potentiaalfunctie. De arbeid die geleverd moet worden om een gesloten kromme te doorlopen in het krachtveld van een centrale kracht is immers altijd 0. Dit wordt geïllustreerd met de kromme ABCD in de figuur. Bij verplaatsen over de boogjes AB en CD staat de kracht loodrecht op de verplaatsing en is er dus geen arbeid. Voor elk punt van het rechte stuk BC is er een overeenkomstig punt van DA waarop dezelfde kracht aangrijpt, maar dat in tegengestelde zin doorlopen wordt. De bijdragen over BC en DA vallen dus tegen elkaar weg. De totale arbeid is dus 0.

Meer wiskundig kan men stellen dat de rotor van een kracht alleen kan verschillen van 0 als een bepaalde component van de kracht functie is van één of meer andere componenten van de positie. In cartesische coördinaten betekent dat bv. dat de x-component van de kracht moet functie zijn van de y- of z-component van de positie. Voor bolcoördinaten betekent het dat de radiale component moet functie zijn van de hoeken θ of φ. Maar bij een centrale kracht is er alleen een radiale component en die is alleen functie van r.

Voor een voorwerp dat beweegt in een centraal krachtveld geldt dus de wet van behoud van energie. Zoals in het hoofdstuk over elementaire dynamica aangetoond werd, kan de de potentiële energie van de gravitatie geschreven worden als

$E_{p}=-G{\frac {m_{1}m_{2}}{r}}+C$

Bij de klassieke ijking stelt men deze potentiële energie gelijk 0 voor r = oneindig. Op die manier wordt C = 0 en hoeft men geen constante mee te nemen. Het gevolg is wel dat voor alle reële afstanden de potentiële energie negatief is en dat men wel moet bedenken dat -100 kleiner is dan -10. Voor een voorwerp dat zich juist kan onttrekken aan de gravitatiekracht van de aarde zal de totale energie = 0 zijn. Hoe dit bekomen wordt kan men zien in het voorbeeld dat uitgerekend wordt na de berekening van deze potentiële energie in het hoger vermelde hoofdstuk. Deze eigenschap zal verder gebruikt worden bij het berekenen van de excentriciteit van een baan.

Een tweede merkwaardige eigenschap is dat voor een cirkelbaan de kinetische energie de helft is van de (absolute) waarde van de potentiële energie. Bij een cirkelbaan zorgt de gravitatiekracht voor de normale versnelling:

$G{\frac {m_{1}m_{2}}{r_{c}^{2}}}=m_{2}v^{2}/r_{c}$

Hieruit volgt dadelijk $v_{c}^{2}=Gm_{1}/r_{c}\quad$. Als men dit invult in de kinetische energie, krijgt men voor de totale energie van een voorwerp op een cirkelbaan:

$E=E_{p}+E_{k}=-G{\frac {m_{1}m_{2}}{r_{c}}}+{\frac {m_{2}v_{c}^{2}}{2}}=-G{\frac {m_{1}m_{2}}{r_{c}}}+G{\frac {m_{1}m_{2}}{2r_{c}}}=-G{\frac {m_{1}m_{2}}{2r_{c}}}$

Behoud van impulsmoment

Wanneer een voorwerp beweegt onder invloed van een centrale kracht dan moet er behoud van impulsmoment gelden t.o.v. de oorsprong van die kracht. Er kan immers alleen een verandering in impulsmoment van een voorwerp in beweging optreden onder invloed van een moment uitgeoefend door een inwerkende kracht. Maar de centrale kracht heeft geen moment t.o.v. het centrum van die kracht. een voorwerp dat beweegt onder invloed van een centrale kracht moet dus steeds zijn impulsmoment behouden.

Een gevolg hiervan is dat de baan van dat voorwerp in een vlak loodrecht op die impulsmomentvector moet liggen. Wanneer een satelliet gelanceerd wordt met een bepaald vectoriële snelheid, dan bepalen de positievector van dat lanceerpunt en de richting van die snelheid het vlak waarin de satelliet zal bewegen. De beweging zal kan dan best beschreven worden in poolcoördinaten, d.i. als in termen van een afstand r en een hoek θ t.o.v. een referentierichting.

Formule van Binet

Wie niet geïnteresseerd is in de wiskundige afleiding van planetenbanen kan deze paragraaf overslaan.
Wanneer men de bewegingsvergelijkingen van een massa die beweegt in een centraal krachtveld wil opstellen met de methode van Lagrange, dan moet men eerst de kinetische energie opschrijven. In poolcoördinaten wordt dit:

$E_{k}={\frac {\mu }{2}}({\dot {r}}^{2}+r^{2}{\dot {\theta }}^{2})$

Er wordt op dit ogenblik nog geen specifieke kracht ondersteld. Alleen weet men dat de potentiaalfunctie alleen zal afhangen van r en dus kan geschreven worden als V(r). Hiermede kan de Lagrangiaan opgeschreven worden als:

$L={\frac {\mu }{2}}({\dot {r}}^{2}+r^{2}{\dot {\theta }}^{2})-V(r)$

Hieruit volgen dan de twee vergelijkingen:

$\mu r^{2}{\dot {\theta }}=C\quad \quad \quad \quad \quad (1)$

$\mu {\ddot {r}}-\mu r{\dot {\theta }}^{2}+{\frac {\partial V}{\partial r}}=0\quad (2)$

Uit de Lagrangiaan blijkt dat θ een cyclische coördinaat is. Dat leidt dus tot een invariante van de beweging, in dit geval tot het behoud van impulsmoment. De constante C in (1) is niets anders dan het impulsmoment L₀.

Als men de vergelijking van de baan, r = f(θ), wil bekomen, dan doet men dit normaal door de veranderlijke t (tijd) te elimineren tussen de twee opgeloste differentiaalvergelijkingen. Hier zou men echter de differentiaalvergelijking voor de baan willen bekomen zonder die differentiaalvergelijkingen op te lossen. daarvoor wordt beroep gedaan op de kettingregel van het differentiëren:

${\dot {r}}={\frac {dr}{dt}}={\frac {dr}{d\theta }}{\frac {d\theta }{dt}}={\frac {dr}{d\theta }}{\dot {\theta }}$

Hierbij kan men de afgeleide van θ uit (1) halen:

${\dot {\theta }}={\frac {L_{0}}{\mu r^{2}}}$

Hiermede wordt de eerste afgeleide van r:

${\dot {r}}={\frac {dr}{d\theta }}{\frac {L_{0}}{\mu r^{2}}}$

Voor wie ervaring heeft met oplossen van differentiaalvergelijkingen, suggereert deze uitdrukking dat het interessanter kan zijn om over te schakelen op een nieuwe veranderlijke u = 1/r. Men krijgt dan immers:

${\frac {du}{d\theta }}={\frac {-1}{r^{2}}}{\frac {dr}{d\theta }}$

Hiermede kan de vorige uitdrukking herschreven worden als:

${\dot {r}}={\frac {-L_{0}}{\mu }}{\frac {du}{d\theta }}$

Voor de tweede afgeleide van r naar de tijd wordt opnieuw de kettingregel toegepast op deze uitdrukking:

${\ddot {r}}={\frac {d{\dot {r}}}{d\theta }}{\frac {d\theta }{dt}}=\left({\frac {-L_{0}}{\mu }}{\frac {d^{2}u}{d\theta ^{2}}}\right)\left({\frac {L_{0}}{\mu }}u^{2}\right)={\frac {-L_{0}^{2}}{\mu ^{2}}}u^{2}{\frac {d^{2}u}{d\theta ^{2}}}$

De partiële afgeleide van de potentiaalfunctie naar r is niets anders dan de centrale kracht F. Alles invullen in (2) levert:

${\frac {L_{0}^{2}}{\mu }}u^{2}\left({\frac {d^{2}u}{d\theta ^{2}}}+u\right)=-F$

Deze zeer algemene formule staat bekend als de formule van Binet, naar de Franse wiskundige Binet (1786-1856)

Dit wordt nu toegepast voor de gravitatiekracht, die hier eenvoudig zal opgeschreven worden als -kμ/r² = -kμu², met k = G maal de som van de twee massa's. Men krijgt zo de correcte aantrekkingskracht Gm_sm_a/r². (Voor een kunstsatelliet is μ praktisch gelijk aan zijn massa.) Men krijgt als differentiaalvergelijking voor de baan, na wat vereenvoudigen:

${\frac {d^{2}u}{d\theta ^{2}}}+u={\frac {k\mu ^{2}}{L_{0}^{2}}}$

De oplossing hiervan is van de vorm:

$u={\frac {1}{r}}=C.\cos(\theta -\theta _{0})+{\frac {k\mu ^{2}}{L_{0}^{2}}}$

Of in functie van r:

$r={\frac {L_{0}^{2}/k\mu ^{2}}{1+(CL_{0}^{2}/k\mu ^{2})\cos(\theta -\theta _{0})}}$

Hierin zijn C en θ₀ integratieconstanten, die uit de randvoorwaarden moeten bepaald worden. Dit kan vereenvoudigd worden tot:

$r={\frac {p}{1-\epsilon \cos(\theta -\theta _{0})}}$

Dit is de vergelijking van een kegelsnede met een brandpunt in de oorsprong en met excentriciteit ε en met de grote as gedraaid over een hoek θ₀ t.o.v. de referentierichting (normaal de horizontale). Voor wie hiermede niet vertrouwd is volgt hier een kleine uitweiding over de kegelsneden.

De kegelsneden

De kegelsneden zijn een groep krommen die men kan laten ontstaan door een dubbele ronde kegel te laten snijden met een vlak. Als dat vlak evenwijdig is met het grondvlak en loodrecht op de symmetrieas, dan is de snijlijn een cirkel. Laat men het vlak kantelen, dan bekomt men een ellips. Als de het vlak één kegel snijdt en evenwijdig is aan de andere kegel is de snijlijn een parabool. Als beide kegels gesneden worden bekomt men een hyperbool. Men kan een meer uitvoerige uitleg vinden in de Nederlandse Wikipedia onder "Kegelsnede". Een nog beter artikel is te vinden in de Engelse Wikipedia onder "Conics". In het Frans spreekt men van "les coniques". In de figuur is 1=parabool, 2=cirkel en ellips, 3=hyperbool.

1=parabool,2=cirkel en ellips,3=hyperbool

Dikwijls wordt vertrokken van de meest eenvoudige vorm van de vergelijkingen voor deze krommen. In een klassiek cartesisch assenkruis worden die:

• voor de ellips:
  

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$
Voor y = 0 (snijpunten met de x-as) krijgt men dat x moet gelijk zijn aan +a of -a. De parameters a is dus de halve as in de x-richting. Analoog is b de halve as in de y-richting. Indien a = b heeft men een cirkel. De vergelijking wordt dan geschreven als
$x^{2}+y^{2}=r^{2}\quad$ met R de straal van de cirkel.

• voor de parabool
  

$\textstyle y=ax^{2}$
Voor x = +1 of -1 is y = a. De parameter a bepaalt dus hoe sterk de parabool opengaat. Voor x gaande naar oneindig gaat ook y naar oneindig. Men zegt dat de parabool raakt aan de kromme op oneindig, voor deze formulering in de richting van positieve y-as.

• voor de hyperbool
  

${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1$
Voor y = 0 krijgt men weer dat x moet gelijk zijn aan +a of -a. Maar voor x = 0 moet men de wortel trekken uit -b². Dat levert dus zogenaamde imaginaire punten op.

De krommen kunnen ook beschreven worden in poolcoördinaten. Dan hebben alle kegelsneden de vorm:

$r={\frac {p}{1+\epsilon \cos(\theta )}}$

Hierin is ε de excentriciteit. Naargelang de grote van deze parameter kan men volgende gevallen onderscheiden:

• ε = 0 : de vergelijking van een cirkel. Hieraan is dus niets excentriek. In feite staat er dan geen echte vergelijking meer maar alleen r = p.
• 0 < ε < 1 : een ellips
• ε = 1 : een parabool. Voor θ = 180° wordt cos θ = -1. De noemer heeft dan een nulpunt en r gaat dus naar oneindig.

Hyperboolbaan bij aantrekkingskracht

Voor ε > 1 heeft men een hyperbool. Maar hier liggen de zaken iets moeilijker. In de mechanica moet bij poolcoördinaten r altijd positief zijn. Als θ = 180° heeft men een negatieve r en dat is dus niet toegelaten. Men krijgt dus maar 1 tak van de hyperbool. In de meetkunde aanvaarden sommige auteurs een negatieve r bij poolcoördinaten. Dan levert de zone rond θ = 180° de andere tak. Aan de rand van de verboden zone wordt de noemer nul en gaat r dus naar oneindig. Deze richtingen worden de asymptotische richtingen genoemd. Bij een aantrekkende kracht ligt het aantrekkingscentrum in het brandpunt binnen de toegelaten hyperbooltak. Later zal gezien worden dat bij afstotende krachten het afstotingscentrum in het brandpunt buiten de toegelaten hyperbooltak ligt.

ellips met alle parameters

Een ellips kan ook gedefinieerd worden als de verzameling van alle punten zodat de som van de afstanden tot twee gegeven punten constant is. Die twee punten noemt men de brandpunten of foci van de ellips. Een geanimeerde voorstelling hiervan kan men vinden als de ellips van de tuinman.

De planetenbanen zijn meestal ellipsen. Voor een ellips kan men nog volgende elementen definiëren:
- de halve grote as a
- de halve kleine as b
- de afstand van een brandpunt tot de meest nabije top van de ellips (A): r₁. Wordt hier bereikt bij θ = 0°. Bij een satelliet die rond de aarde draait noemt men dit het perigeum, voor een planeet die rond een zon draait het perihelium (van de Griekse woorden γη = aarde en ἑλιος = zon en περι = dichtbij)
- de afstand van een brandpunt tot de verste top van de ellips (C): r₂. Wordt hier bereikt bij θ = 180°. Bij een satelliet die rond de aarde draait noemt men dit het apogeum, voor een planeet die rond een zon draait het aphelium (van de Griekse woord απο = ver weg).

Nota: de vergelijking kan ook opgeschreven worden met een minteken in de noemer. Dan wordt alles gespiegeld t.o.v. de kleine as. De ellips wordt dan beschreven vanuit F₂, met r₁ naar links bij θ = 180° en r₂ naar rechts bij θ = 0°

Tussen deze elementen bestaan volgende betrekkingen:

$2a=r_{1}+r_{2}\quad \quad b={\sqrt {r_{1}.r_{2}}}$

Voor het omrekenen van r₁ en r₂ naar a en b moet men een vierkanstvergelijking oplossen:

$\textstyle x^{2}-2ax+b^{2}=0$

met als oplossing:

$r_{1}=a-{\sqrt {a^{2}-b^{2}}}$

$r_{2}=a+{\sqrt {a^{2}-b^{2}}}$

Voor de excentriciteit heeft men: $\epsilon ={\frac {\sqrt {a^{2}-b^{2}}}{a}}={\frac {r_{1}-r_{2}}{r_{1}+r_{2}}}$

De oppervalkte van een ellips is πab .

Voorbeeld
Indien de assen gegeven zijn als a = 5 cm en b = 3 cm dan krijgt men

$r_{1}=a-{\sqrt {a^{2}-b^{2}}}=5-{\sqrt {25-9}}=1\,\mathrm {cm}$

$r_{2}=a+{\sqrt {a^{2}-b^{2}}}=5+{\sqrt {25-9}}=9\,\mathrm {cm}$

$\epsilon ={\frac {\sqrt {a^{2}-b^{2}}}{a}}={\frac {\sqrt {25-9}}{5}}=0,8$

$\epsilon ={\frac {r_{1}-r_{2}}{r_{1}+r_{2}}}={\frac {1-9}{1+9}}={\frac {8}{10}}$

Ter controle:

$\textstyle 2a=10\,\mathrm {cm} =r_{1}+r_{2}=1+9=10\,\mathrm {cm}$

$b=3\,\mathrm {cm} ={\sqrt {r_{1}.r_{2}}}={\sqrt {1.9}}=3\,\mathrm {cm}$

Satellietbanen

Men moet nu deze formule betrekken op de lanceerpositie en -snelheid van de satelliet. er wordt ondersteld dat de satelliet door een raket in een bepaald beginpunt van de baan gebracht wordt met een bepaalde beginsnelheid. In wat volgt wordt dit de lanceerpositie genoemd. r₀ is de afstand tot de lanceerpositie, v₀ de snelheid in dat punt en φ de hoek met de aardstraal door dat punt. Men heeft dan:

$L_{0}=\Vert {\vec {r}}_{0}\times \mu {\vec {v}}_{0}\Vert =\mu v_{0}.r_{0}.\sin \varphi$

De baan van een planeet of satelliet is in feite onafhankelijk van de massa. Alleen zal er meer energie nodig zijn om een zware satelliet een zelfde lanceersnelheid mee te geven vanuit dezelfde lanceerpositie dan een lichter satelliet. In de uitdrukkingen die opgesteld werden komt dikwijls de breuk L₀/μ voor. Daar μ in teller en noemer voorkomt, zal dit in het vervolg vervangen worden door c = L₀/μ; c is dus ook een constante.

$\textstyle c=\Vert {\vec {r}}_{0}\times {\vec {v}}_{0}\Vert =v_{0}.r_{0}.\sin \varphi$

$p={\frac {c^{2}}{k}}={\frac {v_{0}^{2}.r_{0}^{2}.\sin ^{2}\varphi }{k}}$

Om de excentriciteit te kunnen betrekken in de vergelijkingen, wordt de snelheid uitgerekend. Dit is een vrij omslachtige berekening, die niet wiskundig geïnteresseerden kunnen overslaan.

In poolcoördinaten geldt:

$v^{2}={\dot {r}}^{2}+(r{\dot {\theta }})^{2}$

De radiale snelheid wordt, zoals hoger, berekend via de kettingregel en met gebruik van rω² = c (behoudvan impulsmoment):

${\dot {r}}={\frac {dr}{dt}}={\frac {dr}{d\theta }}{\frac {d\theta }{dt}}={\frac {dr}{d\theta }}.{\frac {c}{r^{2}}}$

$\quad \quad ={\frac {\epsilon .c.sin(\theta -\theta _{0})}{p}}$

Uiteindelijk bekomt men:

$v^{2}={\frac {\epsilon .c.sin(\theta -\theta _{0})}{p}}+{\frac {c^{2}[1+\epsilon \cos(\theta -\theta _{0})]^{2}}{p^{2}}}$

Na nog wat rekenwerk haalt men hieruit:

$\epsilon ^{2}-1={\frac {c^{2}}{k^{2}}}(v^{2}-{\frac {2k}{r}})\quad \quad \mathrm {(A)}$

Hoger werd bij het behoud van energie reeds opgemerkt dat de minimale snelheid opdat een voorwerp zich zou onttrekken aan de gravitatiekracht van de aarde gegeven wordt door:

${\frac {\mu v^{2}}{2}}={\frac {k\mu }{r}}\quad \mathrm {of} \quad v_{\infty }={\sqrt {\frac {2k}{r_{0}}}}$

Om de berekeningen te vereenvoudigen wordt nu de verhouding q ingevoerd gedefinieerd als:

$q_{0}={\dfrac {v_{0}^{2}}{v_{\infty }^{2}}}$

Voor een cirkel moet q₀ = 1/2, om de reden die hoger bij behoud van energie vermeld werd.

Invoeren van deze q₀ in de vergelijking voor ε leidt tot:

$\textstyle \epsilon ^{2}=1-4q_{0}(1-q_{0})\sin ^{2}\varphi \quad \quad \mathrm {(B)}$

Hiervan mag alleen de positieve wortel gebruikt worden. Bemerk dat men voor een cirkelbaan steeds loodrecht op de straal moet lanceren, dus met φ = 90°, want de raaklijn aan een cirkel staat altijd loodrecht op de straal.

lanceerposities voor een satelliet

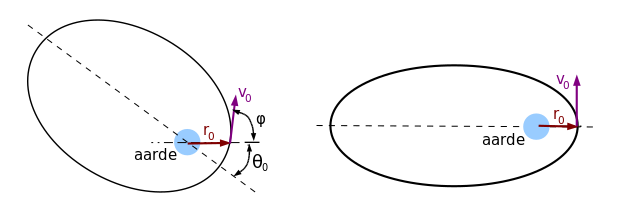
Men kan de vergelijking van de baan dan herschrijven als:

$r={\frac {2.r_{0}.q_{0}.\sin ^{2}\varphi }{1+\epsilon \cos(\theta -\theta _{0})}}$

De hoek θ₀ kan berekend worden uit de vergelijking van de ellips door r = r₀ te stellen en θ = 0. Men krijgt:

$\cos \theta _{0}={\frac {1-2q_{0}\sin ^{2}\varphi }{\epsilon }}$

Het perigeum wordt gegeven door

$r_{1}={\frac {2.r_{0}.q_{0}.\sin ^{2}\varphi }{1+\epsilon }}$

Voor het agogeum heeft men:

$r_{2}={\frac {2.r_{0}.q_{0}.\sin ^{2}\varphi }{1-\epsilon }}$

De som van beide is 2a. M.b.v. a kan de omlooptijd berekend worden, zoals verder zal getoond worden. De halve kleine as is dan

$b=a{\sqrt {1-\epsilon ^{2}}}={\sqrt {r_{1}.r_{2}}}$

Er zal later aangetoond worden dat zowel de totale kinetische energie als de omlooptijd alleen afhangen van de halve grote as a. Daar de kinetische energie niet beïnvloed wordt door de hoek φ, blijven omloopstijd en grote as onveranderd bij verschillende waarden van φ.

De formules worden sterk vereenvoudigd als men lanceert loodrecht op de aardstraal. Dit betekent dat men ofwel in het perigeum of in het apogeum lanceert. dan wordt sin φ = 1, θ₀ = 0 en men krijgt:

$\epsilon ^{2}=1-4q_{0}+4q_{0}^{2}$

Men kan controleren dat voor q₀ = 1/2, ε = 0 wordt, zoals vereist voor een cirkelbaan. Als q₀ groter is dan 1/2 dan lanceert men vanuit het perigeum, als q₀ kleiner is dan 1/2 dan lanceert men vanuit het apogeum. Om een positieve ε te krijgen moet men dus schrijven:

$\textstyle \epsilon =1-2q_{apogeum}\quad {\mbox{of}}\quad \epsilon =2q_{perigeum}-1$

Men krijgt verder:

$r_{apo}={\frac {2r_{peri}q_{peri}}{1+\epsilon }}$

$r_{peri}={\frac {2r_{apo}q_{apo}}{1-\epsilon }}$

Voorbeeld

Men moet voor de numerieke voorbeelden bedenken dat r gemeten wordt vanaf het centrum van de aarde. Als R_a de straal is van de aarde en h de hoogte boven het aardoppervlak, dan r = R_a + h Voor de de aarde is k = 4,0.10¹⁴ m³/s² (MKS eenheden) en R_a = 6370 km.

Een satelliet wordt gelanceerd loodrecht op de aardstraal op een hoogte van 400 km met een snelheid van 8,8 km/s. Bereken de elementen van de baan.

Oplossing:
r₀ = 6370 + 400 = 6770 km = 6,77.10⁶ m
$q_{0}={\frac {v_{0}^{2}}{v_{\infty }^{2}}}={\frac {(8,8.10^{3})^{2}}{2.4.10^{14}/6,77.10^{6}}}={\frac {524,27}{800}}=0,6553$
q₀ is groter dan 1/2: er wordt gelanceerd vanuit het perigeum.
$\textstyle \epsilon =2q_{per}-1=2.0,6553-1=0,3061$
$r_{apo}={\frac {2r_{peri}q_{peri}}{1+\epsilon }}={\frac {2.6,77.10^{6}.0,6553}{1-0,3061}}=12870\ \mathrm {km}$
h_apo = 12870 - 6370 = 6500 km
De dubbele grote as : 6770 km + 12870 km = 19640 km. Halve grote as a = 9820 km
$b={\sqrt {6770.12870}}=9334\ \mathrm {km}$

De wetten van Kepler

Johannes Kepler (1517 - 1630) Gaf voor het eerst een nauwkeurige beschrijving van de banen van de planeten. Later zouden deze dienen als voornaamste inspiratie van het werk van Newton. Zijn ideeën zijn vervat in zijn drie wetten:

• De baan van een planeet is een ellips met de zon in een brandpunt
• De lijn die de zon met de planeet verbindt, doorloopt gelijke oppervlakten in gelijke tijden. Dit wordt ook wel de perkenwet genoemd.
• De kwadraten van de omloopstijden verhouden zich als de derde machten van de halve grote as.

perkenwet

De eerste wet is hierboven afgeleid en reeds uitvoerig gebruikt. Voor de tweede wet wordt beroep gedaan op het vectorieel product. Als een planeet (of satelliet) gedurende een tijd Δt een verplaatsing Δr ondergaan heeft, dan is de oppervlakte van de begrensd door r, Δr en (r+Δr) de helft van het parallellogram dat men kan construeren met r en Δr. Als men de oppervlakte hiervan voorstelt als ΔA, dan volgt uit de eigenschappen van het vectorieel product dat

$\Delta A={\frac {1}{2}}\Vert {\vec {r}}\times {\vec {\Delta r}}\Vert$

Delen door Δt en overgaan naar de limiet voor Δt gaande naar 0:

${\frac {dA}{dt}}={\frac {1}{2}}\Vert {\vec {r}}\times {\vec {v}}\Vert$

Uit behoud van impulsmoment bij de planetenbeweging volgt echter dat het rechterlid constant is. Waarmede de perkenwet bewezen is.

Deze wet betekent dat een planeet of satelliet sneller zal bewegen als hij dichter bij het aantrekkend hemellichaam komt en trager naarmate hij er zich van verwijdert. Een mooie animatie hiervan kan men vinden op http://surendranath.tripod.com/GPA/Dynamics/Kepler01/Kepler01.html .

Voor de derde wet moet eerst de omlooptijd berekend worden. Hiervoor wordt de vorige uitdrukking geïntegreerd over een volledige omwenteling:

$\int dA=\int _{0}^{T}(c/2)dt\quad {\mbox{waaruit}}\quad \pi ab=cT/2$

met T de gevraagde periode van de planeet of satelliet. In de gevonden uitdrukking zitten echter drie elementen van de baan, nl. a, b en c. Daartussen bestaan verbanden die moeten toelaten om de formule eenvoudiger te schrijven. Men heeft

$p={\frac {c^{2}}{k}}\quad {\mbox{of}}\quad c^{2}=pk$

Als men de uitdrukking voor T herschikt en kwadrateert:

$T^{2}={\frac {4\pi a^{2}b^{2}}{c^{2}}}={\frac {4\pi a^{2}b^{2}}{pk}}$

$a={\dfrac {r_{1}+r_{2}}{2}}={\frac {1}{2}}\left({\frac {p}{1+\epsilon }}+{\frac {p}{1-\epsilon }}\right)={\frac {p}{1-\epsilon ^{2}}}\quad \quad \mathrm {(C)}$

Anderzijds heeft men ook:

$1-\epsilon ^{2}={\frac {b^{2}}{a^{2}}}$

Substitueert men dit in vorige uitdrukking dan krijgt men de formule voor de omlooptijd:

$T^{2}={\frac {4\pi ^{2}a^{3}}{k}}$

Dit bevestigt de derde wet van Kepler. Een animatie over deze derde wet kan men vinden op http://surendranath.tripod.com/GPA/Dynamics/Kepler03/Kepler03.html

Voorbeeld 1
Op welke hoogte en met welke snelheid moet men een satelliet lanceren als men hem in een cirkelvormige baan wil hebben met een omlooptijd van 8 u.

Oplossing:
8 u = 8*3600s = 28800 s
Bij een cirkelbaan is a ook de straal van de cirkel:
$a=\left({\frac {T^{2}k}{4\pi ^{2}}}\right)^{\frac {1}{3}}=\left({\frac {28800^{2}.4.10^{14}}{4\pi ^{2}}}\right)^{\frac {1}{3}}=20331\ \mathrm {km}$
hoogte = 20331 - 6370 = 13961 km boven het aardoppervlak
$v={\sqrt {\frac {k}{r}}}={\sqrt {\frac {4.10^{14}}{20,331.10^{6}}}}=4435\ \mathrm {m/s}$

Voorbeeld 2
Bereken de omlooptijd van de satelliet uit het voorbeeld aan het einde van vorige paragraaf.

Oplossing: Gegeven: a = 9820 km
$T=\left({\frac {4\pi a^{3}}{k}}\right)^{0.5}={\frac {2\pi (982.10^{4})^{\frac {3}{2}}}{2.10^{7}}}={\frac {\pi .982^{\frac {3}{2}}}{10}}=9667\ {\mbox{s}}=2\,{\mbox{u}}\ 41\,{\mbox{min}}\ 7\,{\mbox{s}}$

Totale energie

Er wordt nu aangetoond dat de totale energie enkel afhangt van de halve grote as a. In het begin van dit hoofdstuk werd er reeds aan herinnerd dat de potentiële energie in een gravitatieveld kan geschreven worden als -km/r. Voor de kinetische energie wordt teruggekeerd naar de formule A hierboven, die opgelost wordt naar v²:

$v^{2}={\frac {k^{2}}{c^{2}}}(\epsilon ^{2}-1)+{\frac {2k}{r}}$

Hoger werd onder C afgeleid dat

$a={\frac {p}{1-\epsilon ^{2}}}$

en anderzijds is er p = c²/k . Vult men dat alles in in vorige uitdrukking dan krijgt men:

$v^{2}={\frac {-k}{a}}+{\frac {2k}{r}}$

$E_{kin}={\frac {mv^{2}}{2}}={\frac {-mk}{2a}}+{\frac {mk}{r}}$

$E_{totaal}=E_{kin}+E_{pot}={\frac {-mk}{2a}}+{\frac {mk}{r}}-{\frac {mk}{r}}={\frac {-mk}{2a}}$

Deze betrekking zou dus ook kunnen gebruikt worden om de grote as uit te rekenen en daarmede dan de omlooptijd. Men kan ook gemakkelijk controleren dat de formule klopt voor een cirkelbaan. Het blijkt dus dat de lanceringshoek φ geen invloed heeft op de grote as noch op de omlooptijd, maar alleen op de excentriciteit van de baan.

Aarde niet raken

De eis dat de aarde niet mag geraakt worden komt neer op het eisen dat r_perigeum groter moet zijn dan R_a, de straal van de aarde.

$R_{a}={\frac {2r_{0}q_{0}\sin ^{2}\varphi }{1+\epsilon }}$

Deze uitdrukking wordt opgelost naar ε

$\epsilon ={\frac {2r_{0}q_{0}\sin ^{2}\varphi }{R_{a}}}-1$

Als men deze uitdrukking kwadrateert, kan men ε² vervangen door de uitdrukking uit B. Verder uitwerken en rekening houdend met r₀ = R_a + h levert:

$q_{0}>q_{crit}={\frac {R_{a}.h}{(R_{a}+h)^{2}\sin ^{2}\varphi -R_{a}^{2}}}$

Daar ondersteld wordt dat men niet in het perigeum lanceert, moet deze uitdrukking groter blijven dan 0,5.

Wanneer men loodrecht op de aardstraal lanceert, dan vereenvoudigt deze formule zich tot:

$q_{crit}={\frac {R_{a}.h}{(R_{a}+h)^{2}-R_{a}^{2}}}={\frac {1}{2+h/R_{a}}}$

Overgangsbaan

Hohmann transfer orbit

Reeds in 1925 had een mijnheer Hohmann uitgerekend hoe een ruimtetuig met behulp van twee versnellingen naar een eerste cirkelbaan naar een andere cirkelbaan zou kunnen overgebracht worden. Men noemt deze baan daarom de Hohmann overgangsbaan of in het Engels "Hohmann transfer orbit".

De berekening maakt gebruik van de hoger vermelde formule voor de totale energie, die hier herschreven wordt als:

${\frac {mv^{2}}{2}}-{\frac {km}{r}}={\frac {-mk}{2a}}$

Opgelost naar v² levert dit:

$v^{2}=k\left({\frac {2}{r}}-{\frac {1}{a}}\right)$

Voor de eerste cirkelbaan met straal r₁ heeft men natuurlijk dat v₁ = k/r₁. Voor de snelheid op de ellipsvormige baan in het apogeum moet gelden:

$v_{p}^{2}=k\left({\frac {2}{r_{1}}}-{\frac {2}{r_{1}+r_{2}}}\right)={\frac {2kr_{2}}{r_{1}(r_{1}+r_{2})}}$

In het onderste punt, het perigeum voor de ellipsbaan, moet de snelheid van het ruimtetuig dus opgevoerd worden met een waarde:

$\Delta v_{p}=v_{p}-v_{1}={\sqrt {\frac {2kr_{2}}{r_{1}(r_{1}+r_{2})}}}-{\sqrt {\frac {k}{r_{1}}}}={\sqrt {\frac {k}{r_{1}}}}({\sqrt {\frac {2r_{2}}{r_{1}(r_{1}+r_{2})}}}-1)$

Analoog heeft men voor het bovenste punt van de ellipsbaan:

$v_{a}^{2}=2k{\frac {r_{1}}{r_{2}(r_{1}+r_{2})}}$

En voor de versnelling in het apogeum vindt men:

$\Delta v_{a}=v_{2}-v_{a}={\sqrt {\frac {k}{r_{2}}}}(1-{\sqrt {\frac {2r_{1}}{r_{2}(r_{1}+r_{2})}}})$

De tijd die nodig is voor de overgang is de helft van de omloopstijd op de ellipsbaan:

$T_{H}=\pi {\sqrt {\frac {(r_{1}+r_{2})^{3}}{8k}}}$

De 8 in de noemer is afkomstig van de derde macht van de noemer in a=(r₁+r₂)/2.

Meer hierover kan men vinden in het artikel van de Engelse wikipedia Hohmann transfer orbit

De parametervergelijking

parametervergelijking voor de ellips

Er bestaat een parametervergelijking voor de ellips:

${\begin{matrix}\textstyle x=a\cos \theta \\\textstyle y=b\sin \theta \end{matrix}}$

Dit kan grafisch uitgewerkt worden in een constructie met twee concentrische cirkels, één met straat a en de andere met straat b. Vanuit het gemeenschappelijk centrum wordt een lijn getrokken onder een hoek θ die beide cirkels snijdt. Het snijpunt met de grote cirkel levert de x-coördinaat, het snijpunt met de kleine cirkel de y-coördinaat. Bemerk dat de lijn zelf normaal niet door het punt van de ellips wijst dat zo bepaald werd. De hoek θ die hier gebruikt wordt heeft dus niets te maken met de θ uit de vergelijking in poolcoördinaten.

Afstotingskracht

De formule van Binet kan ook gebruikt worden voor een afstotende kracht. Wanneer het gaat om een afstotende kracht die afneemt met het kwadraat van de afstand, vindt men als baan altijd een hyperbooltak. Er zijn nog wat verschillen met de vorige behandeling. Bij de aantrekkingskracht werd vooral het berekenen van banen van satellieten beoogd. Hiervoor werd de onderstelling gebruikt dat de massa van de satelliet verwaarloosbaar is t.o.v. de massa van de planeet. Bij afstotende krachten gaat het echter meestal over microscopische fenomenen, zoals de afstoting van een elektron door een ander negatief geladen deeltje. De vermelde onderstelling gaat dan niet meer op.

Wanneer men opnieuw vertrekt van de formule van Binet, dan heeft een afstotende kracht een positieve projectie te hebben op de r-as. De term in het rechterlid wordt dus negatief. Om dit voor de lezer duidelijker te maken zal dit rechterlid daarom geschreven worden als -k'/r² of -k'u². De kracht is k'/r². Normaal wordt hier gewoon k gebruikt i.p.v. -k'.

Hyperboolbaan bij afstotende kracht

De algemene formule voor de baan wordt dan:

$r={\frac {-L_{0}^{2}/(k'\mu )}{1+\epsilon \cos(\theta -\theta _{0})}}$

Laat de referentierichting voor θ = 0 zo gekozen worden dat θ₀ = 0 is. ε is hier groter dan 1: het deeltje wordt ondersteld van buiten het krachtveld te komen en het opnieuw te verlaten. Daar r positief moet zijn, zullen alleen de hoeken aanvaardbaar zijn waarvoor de noemer negatief is.

$\textstyle 1+\epsilon \cos \theta <0$

$\cos \theta <{\frac {-1}{\epsilon }}$

Dit betekent dat alleen een bereik rond θ = 180° toegelaten is. Dit betekent dat het afstotingscentrum nu het brandpunt is dat buiten de toegelaten hyperbooltak ligt.

In deze figuur liggen de asymptoten onder een hoek van 30° met de horizontale. cos 30° = 0,866 zodat ε hier 1,1547 zou moeten zijn en de toegelaten hoeken liggen tussen 150° en 210°. Bemerk dat de kleinste afstand tot de hyperbool nu gegeven wordt door 1-ε in de noemer (θ = 180°). Voor de absolute waarde moet men immers schrijven ε-1 en dat is het grootst als de absolute waarde van cos θ = 1 is.

Hyperboolbaan bij afstotende kracht

Bij afstotende krachten wordt de baan meestal gedraaid getekend zodat de asymptoot waarlangs het deeltje nadert horizontaal is. Als β het toegelaten bereik is (hier 60°), dan moet men de figuur dus draaien over β/2 of θ₀ = -β/2.

Om ε te bepalen zal nu beroep gedaan worden op de uitdrukking voor de totale energie. Daar er behoud van energie geldt is dat een invariant van de beweging. Men kan het zich dus gemakkelijk maken en de berekening uitvoeren voor een punt waar die het eenvoudigst is. Dat punt is in het punt dat het dichtst bij het brandpunt ligt, op afstand r₁. De snelheid is normaal de som van een radiale en een transversale component, maar in dat punt is de radiale component = 0. Daar is v = rω, waarbij de hoeksnelheid uit het behoud van impulsmoment gehaald wordt. Dus:

$E_{tot}=T+V={\frac {m}{2}}(r_{1}{\dot {\theta }})^{2}+{\frac {k'}{r_{1}}}$

Hierin moeten volgende substituties uitgevoerd worden:

$r_{1}={\frac {-L_{0}^{2}/k'\mu }{1-\epsilon }}$

${\dot {\theta }}={\frac {L_{0}}{r_{1}\mu }}$

Na wat rekenwerk komt men tot de uitdrukking:

$E_{tot}={\frac {k'^{2}\mu }{2L_{0}^{2}}}(\epsilon ^{2}-1)$

$\epsilon ={\sqrt {1+{\frac {2L_{0}^{2}E_{tot}}{k'^{2}\mu }}}}$

Deze uitdrukking kan ook gebruikt worden bij een aantrekkingskracht mits k'= Gmm'. Bij een aantrekkingskracht is de totale energie = 0 voor een paraboolbaan en negatief voor een ellipsbaan. Men kan gemakkelijk vaststellen dat dit leidt tot resp. een ε = 1 en een ε kleiner dan 1. In de praktijk zal men bij een afstotende kracht de kinetische energie op verre afstand gebruiken waarmede het deeltje nadert

Men kan een mooi applet vinden dat de verstrooiing illustreert kan men vinden op http://www.surendranath.org/GPA/Dynamics/CentralForce/CentralForceOne.html .

Er zal hier niet verder ingegaan worden op het onderwerp van afstotende krachten.