Klassieke Mechanica/Trillingen
Trillingen
[bewerken]Trillingen zijn waarschijnlijk de meest voorkomende beweging. Ze blijven beperkt in de ruimte en in de snelheden die bereikt worden. Daardoor kunnen ze lang blijven doorgaan. Denk bv. aan de slinger van een klok. Trillingen ontstaan wanneer er bij verplaatsing van een massa een terugroepende kracht optreedt, d.i. een kracht die de massa naar haar vertrekpositie wil terugbrengen. Het eenvoudigste geval is een massa aan een veer op een volkomen glad horizontaal oppervlak. Men krijgt dan als bewegingsvergelijking:

Hierin stelt x0 de onbelaste lengte voor van de veer. Als men de oorsprong van de x-as aan het einde van de onbelaste veer neemt, dan verdwijnt deze x0 uit de vergelijking en krijgt men de eenvoudigste vorm. De versnelling wordt hier opgeschreven als een veranderlijke, zonder er een teken aan te geven. Ze kan immers zowel positief als negatief zijn, afhankelijk van de waarden in het rechterlid. Men volgt dus niet de conventies voor het projecteren van onbekende vectoren, zoals die in Statica of in het vorige gedeelte van dit hoofdstuk gebruikt werden.
In het Engels spreekt men, bij de meer theoretische benadering, van "harmonic oscillator" en bij de meer technische werken van "vibrations". Men kan een zeer goed overzicht van deze problematiek vinden op de Engelse Wikipedia onder de titel Vibration.
Lineaire differentiaalvergelijkingen
[bewerken]Deze vergelijking is een tweede orde lineaire differentiaalvergelijking. Een differentiaalvergelijking is een vergelijking die de afgeleiden van een onbekende functie bevat en eventueel die functie zelf. Het is een lineaire differentiaalvergelijking als al deze elementen in de eerste graad voorkomen. Het is een tweede orde differentiaalvergelijking als de hoogste afgeleide een tweede orde afgeleide is.
Wanneer men alleen termen heeft die een afgeleide van de functie bevatten en eventueel de functie zelf, dan spreekt men van een homogene differentiaalvergelijking.
De operator voor differentiëren wordt klassiek geschreven als een breuk, maar kan ook geschreven worden als een D. Zoals men bij de klassieke voorstelling het tweemaal toepassen van de operator schrijft als een tweede macht van de operator, zo schrijft men ook hier een tweede afgeleide als D2.
De vorige vergelijking wordt dan, met de D-operator voor differentiëren naar de tijd, geschreven als:
Om duidelijker te maken naar welke veranderlijke er gedifferentieerd wordt, kan die toegevoegd worden als index, hier dan Dt
Het oplossen van lineaire differentiaalvergelijkingen m.b.v. de D-operator berust op het feit dat de exponentiële functie een eigenfunctie is van deze D-operator. Als een operator toegepast wordt op een eigenfunctie ervan dan is het resultaat een aantal maal deze functie. Men heeft inderdaad:
Vult men de functie
in in de bovenstaande differentiaalvergelijking, met C een willekeurige constante, dan bekomt men:
Tussen de haakjes staat nu een kwadratische vergelijking in λ. Voor de oplossingen hiervan zal aan de differentiaalvergelijking voldaan zijn. De meest algemene oplossing is dan een combinatie van de oplossingen met de verschillende wortels en heeft de vorm:
De constanten Ci zijn de integratieconstanten die uit de beginvoorwaarden, hier de positie en snelheid op t=0, moeten bepaald worden. Er zijn altijd evenveel integratieconstanten te bepalen als de orde van de vergelijking, in dit geval dus 2.
Bij samenvallend wortels moet de algemene oplossing lichtjes aangepast worden. Voor 2 samenvallende wortels wordt de algemene oplossing:
Bemerk de factor t bij C2.
De wortels van de vergelijking in D kunnen reëel of imaginair zijn. Voor reële wortels zal de oplossing een toenemende of afnemende exponentiële functie zijn, voor imaginaire wortels zal men meestal gebruik maken van de identiteit:
Voor de meeste problemen zal men moeten zorgen hiermede een reële oplossing te bekomen. In het algemeen kan men deze reële oplossing schrijven als een combinatie van een sinus- en een cosinusfunctie, met elk een eigen amplitude, of als een sinus- of cosinusfunctie met als integratieconstanten de amplitude en een fasehoek θ0. Dit levert bv. als algemene oplossing voor de bewegingsvergelijking hierboven:
In deze context noemt men ω de pulsatie van de trilling.
Afleiding
De waarden van A.cos ωt en A.sin ωt kunnen bekomen worden door de projectie van een roterende vector met lengte A op resp. de x- en y-as. Wanneer één van deze functies de oplossing is van een tweede orde differentiaalvergelijking, dan moeten er 2 integratieconstanten zijn. Deze worden dan gegeven als de lengte van de roterende vector en de hoek ervan op t = 0. Deze laatste noemt men ook de fazehoek. Hij wordt in technische toepassingen meestal weergegeven door de Griekse letter φ i.p.v. θ0.
Voor imaginaire wortels ± λ zal men de oplossing moeten schrijven als:
Deze oplossing zal reëel zijn als A = B en α = β. Die reële oplossing wordt dan:
Natuurlijke trilling
[bewerken]Als men het trillen van de massa in gang zet door de massa in haar rustpositie een zekere beginsnelheid v0 te geven, dan worden de beginvoorwaarden (situatie voor t=0) : x(0) = C cos(0 + θ0) = 0 en v0 = -C ω sin(θ0). Uit de eerste vergelijking volgt dat θ0 = ± 90°. Men kan dan beter een sinusfunctie gebruiken:
De beginvoorwaarden worden dan: x(0) = C.sin(θ0)=0, waaruit θ0 = 0, en v0 = C ωcos(0), waaruit C = v0/ω . Men krijgt dus als bewegingsvergelijking:
Een beweging die verloopt volgens een sinus- of cosinusfunctie noemt men een harmonische beweging. Men kan hiervoor nog volgende grootheden definiëren:
- de frequentie f = het aantal trillingen per seconde. f = ω/2π
- de periode T = de tijd nodig voor 1 trilling (in seconden). T = 1/f = 2π/ω
Men heeft ook ω = 2πf
Zet men de beweging in gang door de massa los te laten in een beginpositie die niet overeenkomt met de onbelaste lengte van de veer, dan zal men de oplossing eerder met een cosinsufunctie opschrijven.
Massa hangend aan een veer
[bewerken]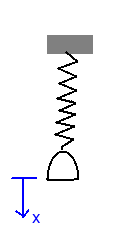
Een meer realistisch voorbeeld krijgt men met een massa die aan verticale veer hangt. Men heeft dan als bewegingsvergelijking, mits de oorsprong opnieuw in het eindpunt van de onbelaste veer te leggen en met x-as naar beneden:
In deze vergelijking komt nu een term voor die noch de functie x(t) noch een afgeleide ervan bevat. Als men de differentiaalvergelijking schrijft met de D-operator, dan wordt deze term in het rechterlid gezet:
Dit is geen homogene vergelijking meer. De oplossing ervan is een combinatie van de oplossing van de vergelijking met het rechterlid = 0, de homogene vergelijking, en de oplossing met het rechterlid verschillend van 0. De oplossing voor de homogene vergelijking is bekend van hierboven. Daar het rechterlid hier een constante is, zal de oplossing voor de vergelijking met rechterlid ook gewoon een constante zijn. Men krijgt dan kx = mg of x = mg/k. Dit is niets anders dan de nieuwe evenwichtspositie. De som van beide oplossingen zegt dus dat de massa nu zal trillen rond de nieuwe evenwichtspositie met dezelfde amplitude en frequentie (bij gelijke beginvoorwaarden) als in het vorige geval. Dit werd ook reeds als resultaat bekomen bij het voorbeeld op het einde van de paragraaf over de berekening van enkele potentiële energieën .Een constante kracht heeft geen invloed op de frequentie van de trilling.
Men kan deze constante laten verdwijnen uit de vergelijking als men de oorsprong van het assenstelsel in de nieuwe evenwichtsstand legt. De uitrekking van de veer is dan te schrijven als xv + x, waarin xv de uitrekking is tot de nieuwe evenwichtsstand. Dus xv = mg/k. De eerste vorm van de vergelijking wordt dan:
Als men de differentiaalvergelijking wil opschrijven voor een x-as omhoog, dan zou men in eerste instantie moeten schrijven:
Mathematische slinger
[bewerken]Men maakt dikwijls een onderscheid tussen de mathematische en de fysische slinger. De mathematische slinger is een ideaalbeeld van een slinger, opgebouwd uit een gewichtsloze staaf of touw met een puntmassa aan het einde ervan. Bij de fysische slinger werkt men met een reële staaf met aan het einde een reële massa, beide met een gewicht en een traagheidsmoment.

Door projectie op de raaklijn krijgt men als bewegingsvergelijking:
Dit is geen lineaire differentiaalvergelijking want θ komt erin voor als argument van een goniometrische functie. Voor kleine θ kan men echter stellen dat sin θ = θ. Met deze benadering krijgt men wel een lineaire differentiaalvergelijking in θ:
De oplossing zal dus weer een harmonische beweging zijn met periode T = 2π(l/g)1/2. .
Men kan zich afbragen in welke mate de benadering sin θ = θ gerechtvaardigd is. sin θ kan berekend worden met een reeksontwikkeling, waarbij θ natuurlijk in radialen moet uitgedrukt worden:
Er is dus een afwisseling van positieve en negatieve termen. Het speciale van deze reeks is dat, als men de reeks op een bepaald punt afbreekt, de som van alle volgende termen kleiner zal zijn dan de laatste term die men behouden heeft. Dus als men sin θ wil berekenen tot op 1% nauwkeurig, dan moet men termen berekenen tot men een term heeft die 1% of iets minder bijdraagt aan het resultaat. De vraag of de bovenstaande benadering gerechtvaardigd is hangt dus in de eerste plaats af van de gewenste nauwkeurigheid. Hier volgen de waarden voor de eerste en de tweede term van de reeks en hun verhouding:
| Graden | radialen | 2e term | verhouding (%) |
|---|---|---|---|
| 1° | 0,0175 | 8,9 .10-7 | 0,00 051 |
| 2° | 0,0349 | 0,00 000 7 | 0,020 |
| 5° | 0,0873 | 0,00 0111 | 0,127 |
| 10° | 0,1745 | 0,00 088 6 | 0,5077 |
| 15° | 0,2618 | 0,00 299 | 1,142 |
De slinger van een klok beweegt meestal over 1,5 à 2°. Daarvoor is de benadering dus gerechtvaardigd.
Christiaan Huyghens toonde aan dat de slingerperiode constant blijft bij grotere uitwijking als men aan beide zijden van het bevestigingspunt twee "wangen" maakt met de vorm van een cycloïde (1673). (zie Tauchtochtone kromme)
Voor meer ingewikkelde situaties kan men best de methode van Lagrange gebruiken voor het opstellen van de differentiaalvergelijking. Bij systemen waarvoor behoud van energie geldt, kan men ook de totale energie differentiëren naar de tijd. Men krijgt dan een uitdrukking waaruit men een term in de (veralgemeende) snelheid kan afzonderen. De coëfficiënt hiervan levert de bewegingsvergelijking.
Voor de slinger bv. krijgt men voor de totale energie:
Differentiëren naar de tijd levert:
of
Daar ω niet constant 0 is, moet de uitdrukking tussen de haakjes 0 zijn. Dit levert de vergelijking zoals hoger gevonden.
Gedempte trillingen
[bewerken]De trillingen die hier beschreven werden zullen, volgens de gebruikte formules, ten eeuwigen dage doorgaan met dezelfde frequentie en amplitude. Dat strookt niet met onze ervaring. Er ontbreekt een term die een demping van de trilling veroorzaakt. Een frequente situatie is een demping door weerstand in de lucht of in een vloeistof (zie ook "Viskeuze wrijving). Bij lage snelheden levert dit een weerstand die evenredig is met de snelheid:
waarin c de viskeuze dempingscoëfficiënt voorstelt. c heeft als eenheid kg/s. Een demper stelt men grafisch voor door het beeld van een zuiger in een cilinder, zoals in de figuur.
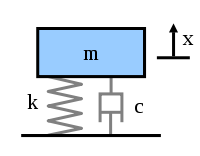
Voor het geval van een massa die opgehangen is aan een veer (zie figuur hier boven!) krijgt men als vectoriële vergelijking:
of als differentiaal vergelijking, met een x-as naar beneden en met oorsprong in het eindpunt van de onbelaste veer:
of met de D-operator:
Voor de oplossing moet men een oplossing zoeken voor de homogene vergelijking, met rechterlid = 0, en een particuliere oplossing voor de vergelijking met rechterlid = mg. Uit vorige berekeningen weet men dat deze laatste bestaat uit een constante uitwijking naar de nieuwe evenwichtspositie. Alleen de homogene vergelijking zal dus behandeld worden.
De oplossing hangt af van de discriminant van deze vergelijking. Deze is:
- Voor δ > 0, heeft men 2 reële wortels. De oplossing is dan een combinatie van 2 exponentiëel dalende functies. Het systeem gaat traag naar zijn nieuwe evenwichtspositie, zonder trillen. Men spreekt van overdemping.
- Voor δ = 0 heeft men 2 samenvallende reële wortels. Het systeem gaat naar zijn evenwichtspositie op de snelste manier waarop dit zonder trillen mogelijk is. Men spreekt van kritische demping
- Voor δ < 0 heeft men complexe wortels. Dit zal een gedempte trilling opleveren.
Om de grens van de kritische demping te berekenen, zou het interessanter zijn om een grootheid te hebben die men kan vergelijken met een absolute waarde zoals 0 of 1. Dit kan door een factor 4k/m af te zonderen. Men krijgt dan:
Stelt men hierin
dan krijgt men voor de vorige uitdrukking:
Men ziet dat de kritische demping nu overeenkomt met ζ = 1. Men noemt ζ daarom de dempingscoëfficiënt. ωn is de natuurlijke pulsatie, d.i. de pulsatie van het ongedempte systeem.
In termen van de m,c en k worden de wortels:
Men kan de vergelijking en de wortels ook herschrijven in functie van ωn en ζ. Men bekomt dan:
De wortels van deze vergelijking worden dan:
Kritische demping
[bewerken]Voor ζ = 1 of c2 = 4km heeft men een kritische demping. Men heeft 2 reële samenvallende wortels. De oplossing moet dan geschreven worden als:
Deze formule geeft de indruk dat de veer geen invloed heeft op de oplossing. c moet echter voldoen aan een betrekking waarin de veerconstante k voorkomt. Vult men deze betrekking in voor c, dan bekomt men dat de wortel gewoon de natuurlijke pulsatie ωn is!
Dit blijkt ook duidelijk uit de tweede formulering voor de wortels met ζ = 1.
Als voorbeeld het gedrag van een systeem dat uit rust vertrekt, bv. een veer waaraan men een gewicht haakt of een weegschaal waarop men een pakje legt. De beginvoorwaarden zijn x(0) = 0 en v(0) = 0. Bedenk dat de volledige oplossing ook de particuliere oplossing x = mg/k bevat. Dit levert voor de integratieconstanten:
Met de numerieke waarden m = 2 kg en k = 400 N/m krijgt men: x0 = -0,05 m; ωn = 14,14 rad; c = 56,56 kg/s; C2 = -0,05*14,14 = 0,707 m. Verder heeft men nog de frequentie f = 2,25 Hz en de periode T = 0,444 s.
De vergelijking wordt:
Deze formule geldt voor een x-as naar beneden. De plot-software kon dat niet weergeven. Voor een x-as omhoog moet alles dus met -1 vermenigvuldigd worden. De plot verloopt nu tussen x=0 en x=-0.05

Men ziet dat het systeem zijn eindtoestand bereikt in iets meer dan de tijd nodig voor 1 periode van de natuurlijke trilling.
De exponent word dikwijls geschreven in termen van de reciproke van de wortel λ, die dan het symbool τ krijgt en de tijdconstante genoemd wordt. Hier is τ = 0,071 s. De vergelijking wordt dan:
Overdemping
[bewerken]Men krijgt nu 2 dalende exponentiële functies, met als algemene vorm:
met xp een eventuele particuliere oplossing. De wortels λ1 en λ2 kan men volgens één van beide hoger gegeven formules berekenen. Voor de snelheid heeft men dan:
Voor het voorbeeld dat gebruikt werd voor de kritische demping en voor een x-as naar boven, krijgt men als vergelijkingen voor de integratieconstanten:
Hieruit kan men de uitdrukkingen voor C1 en C2 afleiden. Dit levert volgende waarden als functie van de dempingscoëfficiënt ζ:
| ζ | λ1 | λ2 | C1 | C2 |
|---|---|---|---|---|
| 1,2 | -7,590 | -26,351 | 0,0702 | -0,0202 |
| 1,5 | -5,402 | -37,025 | 0,0585 | -0,0085 |
| 2,0 | -3,789 | -52,779 | 0,05387 | -0,00387 |
Bemerk dat er steeds voldaan is aan C1 + C2 = 0,05. De eerste figuur toont de bijdrage van de twee exponentiële functies. De volgende figuur toont het totale verloop voor verschillende waarden van ζ.
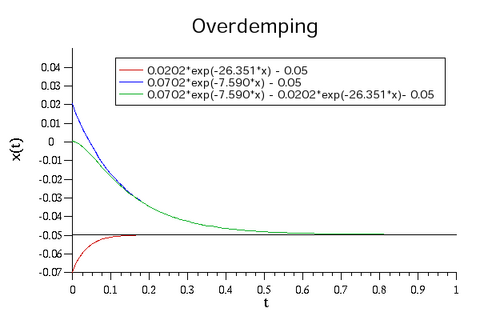

Men ziet duidelijk dat het systeem steeds trager naar zijn evenwichtspositie gaat.
Gedempte trilling
[bewerken]Wanneer de dempingscoëfficiënt kleiner is dan 1 gaat het systeem in een gedempte trilling naar zijn evenwichtsstand. Onder de vierkantswortel in de oplossing voor de wortels staat dan een negatief getal. De wortel hieruit kan men weergeven als het complexe getal iq. De wortels zijn dan van de vorm -p ± iq. Daar
kan men de oplossing van de differentiaalvergelijking schrijven als
Deze oplossing stelt een harmonische beweging voor met exponentieel afnemende amplitude. q is hierbij de pulsatie van de gedempte trilling, voorgesteld door ωd.
Als men de eerste formulering voor de wortels volgt, heeft men:
Volgt men de formulering met de dempingscoëfficiënt ζ en ωn, dan heeft men:
Bemerk dat in beide gevallen de volgorde van de termen onder de vierkantswortel omgewisseld werd om een positief getal onder het wortelteken te bekomen. Men ziet dat ωd kleiner is dan ωn. Met de laatste notatie wordt de algemene vergelijking:
Om nog enige trillingen over te houden moet de dempingscoëfficiënt klein zijn, kleiner dan 0,2. De grafiek hieronder bv. is gemaakt voor een dempingscoëfficiënt van 0,1.
Als voorbeeld wordt opnieuw dezelfde situatie als hierboven gebruikt, maar nu met een lichtjes afgeronde ωn = 15 rad en een ζ = 0,1. Dit geeft een ωd= 14,92 rad. Daar men vertrekt van een begintoestand die een maximum is van de uitwijking wordt met een cosinusfunctie gewerkt.
De grafiek geeft in het rood de dalende exponentiëlen die de omhullende van de trillingen vormen. In het groen de cosinusterm, met een kleine amplitude. Men ziet dat de minima en maxima van de gedempte trilling iets vóór de minima en maxima van de zuivere cosinusterm vallen (iets minder dan 6°, uit hoek voor v = 0) door de afplatting door de exponentiële functie.

Logaritmisch decrement
[bewerken]Wanneer men de verhouding maakt van de amplitudes met een interval van 1 periode Td, dan blijkt dit een constante.
De natuurlijke logaritme van deze verhouding noemt men het logaritmisch decrement:
- (I)
Dit decrement (vermindering) blijkt alleen afhankelijk van de dempingscoëfficiënt ζ, want Td kan geschreven worden in functie van ωn en ζ:
Invullen in vorige formule levert:
Voor zeer kleine waarden van ζ gaat de noemer naar 1 en kan dus weggelaten worden.
Voor het voorbeeld hierboven krijgt men:
De verhouding van de amplitudes is dan:
Men kan dit eventueel controleren op de figuur, tenminste toch voor de eerste 2 cijfers.
Deze formule biedt een mogelijkheid om de dempingscoëfficiënt experimenteel te bepalen. In de praktijk zal men meestal het verschil na meerdere periodes bepalen om de nauwkeurigheid te verhogen. Dan zal men moeten teruggrijpen naar de formule I. In plaats van Td komt dan het tijdsverloop tussen de metingen en d wordt de verhouding tussen de gemeten amplitudes. Als men bv. vaststelt, via decibel metingen, dat een la-snaar (400 Hz) op een gitaar of piano na 3 s teruggevallen is op 1 % van de oorspronkelijke amplitude , dan heeft men:
Gedwongen trillingen
[bewerken]Een zeer belangrijk fenomeen is de reactie van een systeem op een opgelegde trilling. Als men met een auto over een kasseistrook rijdt, dan veroorzaakt dit een trillen dat via de banden en de ophanging ook doorgegeven wordt aan de rest van de carrosserie. Dit kan leiden tot het bekende meerammelen van bepaalde onderdelen. Als het fenomeen alleen optreedt bij een bepaalde snelheid en niet bij een hogere of lagere snelheid, dan heeft men te doen met een fenomeen van resonantie. Iedereen heeft wel het verhaal gehoord van de zangers die een kristallen glas kunnen doen springen door een bepaalde toon te zingen. Ook dat is een fenomeen van resonantie.
Het doorgeven van een trilling aan een ander systeem noemt men de excitatie van dat systeem. Er zal hier alleen over de invloed van een zuivere harmonische excitatie gesproken worden. Bij niet-harmonische excitatie zal men beroep doen op Fourieranalyse van de excitatie. Zie hiervoor bv. Applying "complex" forces to spring-damper model. De manier waarop de trilling doorgegeven wordt aan het systeem heeft niet zoveel belang. Een klassieke opstelling om resonantie te illustreren bestaat uit een klein elektrisch motortje dat onderaan een veer bevestigd wordt. Op de as van dit motortje zit een excentrisch geplaatst gewicht. Bij rotatie ontstaat zo een trilling, waarvan men de frequentie kan regelen via het toerental van de motor. Bij een bepaald toerental ziet men een grote uitwijking van de veer ontstaan. Dan zit men op de resonantiefrequentie. In feite is een elektrische wasmachine, die aan het einde van de wascyclus gaat droogzwieren, een uitvoering hiervan in groot formaat. Ook het trillen van een GSM wordt veroorzaakt door een excentrisch draaiend gewichtje. Bij andere systemen laat men het aangrijpingspunt van de veer een harmonische trilling uitvoeren.
Als basisvoorbeeld wordt opnieuw een massa hangend aan een veer beschouwd. Op het systeem werkt nu een bijkomende uitwendige periodieke kracht met amplitude F en pulsatie ω. De bewegingsvergelijking wordt dan, voor x-as omlaag met oorsprong in de evenwichtsstand (zie ook hoger op het einde van de paragraaf over "Massa hangend aan een veer") :
Of onder de standaardvorm van de differentiaalvergelijking:
Men kan natuurlijk verwachten dat het resultaat ook een periodieke beweging van de massa zal zijn met pulsatie ω. De amplitude zal echter zelden de amplitude F zijn en er is ook meestal een verschil in fase tussen de exciterende kracht en de beweging van de massa.
De algemene oplossing zal bestaan uit een oplossing van de homogene differentiaalvergelijking + een particuliere oplossing. De oplossing van de homogene differentiaalvergelijking kan één van de oplossingen voor de gedempte trilling zijn, zoals hoger beschreven. Meestal gaat het echter over een ondergedempt systeem zodat de oplossing voor de homogene vergelijking een uitstervende trilling is:
Men noemt dit ook wel het transiënte deel van de oplossing.
De particuliere oplossing zal de vorm hebben van een harmonische beweging:
Dit noemt men ook de stabiele of "steady-state" oplossing.
De formules voor de amplitude A en de fasehoek φ blijken vrij ingewikkeld. De afleiding wordt daarom hieronder afzonderlijk gegeven. Het resultaat is een functie van de verhouding tussen de exciterende pulsatie ω en de pulsatie ωn van de natuurlijke trilling van het systeem. Het resultaat kan men opschrijven als:
- met gebruikt van de viskeuze wrijvingscoëfficiënt c en met u = c/2m:
- in functie van de dempingscoëfficiënt ζ en de verhouding ω/ωn:
Hierin komt F/k overeen met de statische uitrekking van de veer door een kracht F
Resonantie
[bewerken]Het is duidelijk dat de amplitude naar een maximum zal gaan als de pulsatie van de exciterende kracht ω gelijk wordt aan de natuurlijke pulsatie ωn van het systeem. Dit verschijnsel heet resonantie. Als er geen demping is, ζ = 0, dan dreigt A zelfs oneindig groot te worden! Het effect kan men best zien door de verhouding van de amplitude A over de statische uitrekking F/k uit te zetten als functie van de verhouding ω/ωn. Men noemt de verhouding Ak/F de amplitudeverhouding of ook wel de versterkingsfactor. De formule hiervoor wordt eenvoudiger als men ω/ωn = r stelt:

De maximale amplitude wordt bereikt voor een minimum van de functie onder het wortelteken in de noemer. Voor ζ = 0 is dit duidelijk bij ωr, de ω bij resonantie, gelijk aan ωn. Voor ζ > 0 verschuift dit minimum. Om het te bepalen moet de afgeleide van de functie gelijkgesteld worden aan 0. Men bekomt:
Juist zoals de eigenpulsatie van een gedempt systeem lager ligt dan de natuurlijke pulsatie, ligt ook hier de resonantiepulsatie lager dan de natuurlijke.
Het verloop van deze krommen wordt in de praktijk duidelijk getoond door een elektrische wasmachine die gaat droogzwieren. Hierbij wordt het toerental van de trommel van 0 opgevoerd tot 1000 t/min en meer. Bij stijgend toerental is er een punt (ergens tussen 300 en 500 t/min) waarop de machine het heftigst schudt. Boven dit toerental vermindert het schudden zeer sterk. Gelukkig voor de fabrikanten van wasmachines wordt dit ook zo voorspeld door de theorie. Het is dus soms veiliger als de trommel aan 1000 t/min draait dan aan 400 !

Het resonantiefenomeen treedt ook op bij elektrische kringen. Het wordt volop gebruikt om bij analoge radio- en TV-toestellen één bepaalde zender uit te pikken. Men begint dan met 2 of 3 kringen, waarvan de resonantiefrequentie door het draaien aan de afstemknop afgestemd wordt op de frequentie van de een bepaalde zender. Deze kringen zorgen voor de koppeling tussen de versterkertrappen, zodat het signaal van de betrokken zender 100 tot 500 maal meer versterkt wordt dan dat van andere zenders. Het ontvangen signaal wordt dan omgevormd naar een vaste middenfrequentie. Daar wordt het opnieuw door 2 of 3 versterkertrappen gestuurd, die gekoppeld zijn door op resonantie afgestemde kringen. Zo wordt telkens opnieuw het gekozen signaal meer versterkt dan de andere signalen, totdat alleen het gekozen signaal nog door ons waargenomen wordt.
Men kan de resonantiepiek typeren door zijn kwaliteitsfactor Q. Deze wordt gedefinieerd als de verhouding van het frequentieverschil tussen de punten waar de amplitude afgenomen is tot 1 over vierkantswortel 2 maal de amplitude van de top, tot de frequentie van de top. Men kan dit opschrijven als:
Men kan aantonen dat voor zwakke demping:
De pianosnaar uit het hoger gebruikte voorbeeld zou hiermede een Q = 820 halen, wat voor een pianosnaar nog aan de lage kant is.
Op het internet zijn verscheidene applets te vinden die het resonantiefenomeen illustreren. Zeer goed is het applet van Walter Fendt, te zien op zijn site op http://www.walter-fendt.de/html5/phnl/resonance_nl.htm .
De meest spectaculaire katastrofe veroorzaakt door resonantie was het instorten van de Tacoma Narrows Bridge. Tacoma is een stadje op een 100 km ten Zuiden van Seatlle in de VS. Warm aanbevolen!
Fasehoek
[bewerken]
De fasehoek tussen aandrijvende kracht en reactie van de massa is ook wat aandacht waard. Als de frequentie van de aandrijvende kracht ver onder de resonantiefrequentie ligt, dan volgt de positie in fase met de aandrijvende kracht. Naarmate men de resonantiefrequentie nadert, komt er een faseverschil dat bij resonantie gelijk wordt aan 90° (=0,5π), onafhankelijk van de dempingsfactor. Maar het vermogen dat door de kracht afgegeven wordt, wordt bepaald door het vectorieel product van kracht met de snelheid: P = F.v. De snelheid is 90° gedraaid t.o.v. de positie en dus in fase met de kracht. Op het ogenblik van de resonantie wordt er dus maximaal energie in het systeem gepompt en dit verklaart natuurlijke het maximum van de amplitude. De veer treedt op als een medium dat (potentiële) energie kan opslaan, maar die deze potentiële energie voortdurend omwisselt voor kinetische.
Voor excitatie met frequenties hoger dan de resonantiefrequentie volgt de massa steeds minder en de fasehoek gaat snel naar 180°. Positie en aandrijvende kracht zijn in tegenfase, De snelheid staat loodrecht op de kracht.
De applets die op het einde van vorige paragraaf vermeld werden, besteden ook allen aandacht aan deze fasehoek.
Belasting van de bevestigingen
[bewerken]Als de veer sterk uitgerokken wordt, oefent ze natuurlijk een grote kracht uit op de massa maar ook op de bevestigingspunten. Een ideale veer beschouwt men als massaloos. Er moeten steeds gelijke en tegengestelde krachten op beide zijden van de veer werken zodat de totale som van de inwerkende krachten 0 is, anders krijgt de veer een oneindig grote versnelling.
De differentiaalvergelijking werkt met de krachten die op de massa uitgeoefend worden. De bevestigingen moeten dezelfde krachten, in grootte en fase, op de veer uitoefenen als de veer en de demper op de massa. Daarom kan men voor de analyse van het probleem werken met de differentiaalvergelijking.
De verschillende krachten die op het systeem werken veranderen echter in de tijd volgens een harmonische functie. Men kan de waarden van die functie beschouwen als ontstaan door de projectie van een roterende vector op een as. Deze roterende vector kan men de genererende vector van die functie noemen. Wanneer men een sinus- of cosinusfunctie differentiëert, ontstaat een functie waarvan de grafiek 90° verschoven is t.o.v. die van de oorspronkelijk functie. Men kan dus zeggen dat die functie gegenereerd wordt door een vector die 90° gedraaid is t.o.v. de vector van de oorspronkelijke functie, in de zin waarin men de hoeken positief rekent. Tot dit besluit is men ook reeds gekomen bij de studie van de cirkelbeweging in het hoofdstuk over Kinematica (zie Kinematica: Toepassing: beweging op een cirkel - Normale en tangentiële versnelling
Men kan nu alle grootheden beschouwen die in de differentiaalvergelijking voorkomen Substitueert men in
de oplossing , dan krijgt men:
Alle grootheden zijn met hun genererende vectoren voorgesteld in de figuur hiernaast.

Op een gegeven ogenblik t1 is ωt = θ1. In de figuur komen 2 belangrijke richtingen voor: de richting bepaald door de hoek θ1 en de hoek bepaald door de richting θ1 - φ. Alleen de kracht ligt volgens de eerste richting, alle andere vectoren zijn betrokken op de tweede richting:
- de kracht kA van de veer ligt volgens de 2e richting, maar het minteken ervoor betekent dat men de vector 180° graden moet draaien.
- de kracht cωA uitgeoefend door de demper is bepaald door een eerste afgeleide en moet dus 90° gedraaid worden t.o.v de 2e richting. Daar er ook een minteken voor staat, wordt het 90° linksom draaien t.o.v. de kracht van de veer.
- het linkerlid, mω2A, is een tweede afgeleide en dus is zijn vector 180° gedraaid t.o.v. de 2e richting. Dit manifesteer zich ook in het minteken in die tweede afgeleide.
De bevestigingen moeten zorgen dat veer en demper op hun plaats blijven. De kracht Fs op die bevestigingen is dus de som van de krachten van veer en demper.
Na enige uitwerking en invullen van de uitdrukking voor de amplitude A als functie van ω vindt men een uitdrukking voor deze kracht als functie van ω. Interessanter is echter de verhouding tussen deze kracht en de aandrijvende kracht. In het Engels spreekt men van "transmissibility". Men vindt:

Voor de eenvoud van de formulering werd opnieuw ω/ωn = r gesteld. Deze uitdrukking gelijkt sterk op de uitdrukking voor de verhouding Ak/F, alleen bevat de teller nu ook een term in r. Alle grafieken beginnen in 1 en alle grafieken passeren opnieuw door 1 voor r = wortel 2 (=1,414). Dit betekent dat men liefst zorgt dat het systeem werkt in de zone rechts van dit punt. Bemerk ook dat, in die zone, de verhouding groter wordt met grotere demping. Dit is te begrijpen omdat de snelheid hier groter wordt. Uit vorige grafieken blijkt ook dat de aandrijvende kracht nog weinig energie in de veer pompt in dit gebied.
Multimodale trillingen
[bewerken]Een systeem van 3 veren en 2 massa's kan men op 2 manieren laten bewegen: men kan de eerste massa stil houden en de tweede bewegen of omgekeerd. Men zegt dat het systeem 2 vrijheidsgraden heeft. Systemen met meerdere vrijheidsgraden kunnen ook op verscheidene manieren trillen. Men spreekt van trillingsmodes. In het Engels heten vrijheidsgraden "degrees of freedom", wat dikwijls afgekort wordt tot "DOF".

Voor de eenvoud van de zaak worden volgende onderstellingen gemaakt:
- alle veren hebben dezelfde onbelaste lengte
- wanneer het systeem in rust is, hebben alle veren hun onbelaste lengte.
De positie van elke massa wordt gegeven t.o.v. haar evenwichtspositie. Om te beginnen wordt de demping weggelaten. Op de eerste massa werkt een kracht van de eerste en de tweede veer. De lengte van de tweede veer wordt gegeven door |x2 - x1|.
Op de tweede massa werkt een kracht van de tweede en de derde veer:
Voorbeeld
Als men verder onderstelt dat men twee gelijke massa's heeft en dat alle veren zelfde stijfheid hebben, dan krijgt men het stelsel:
Men onderstelt nu dat de oplossing een harmonische trilling is met zelfde frequentie voor beide massa's maar eventueel verschillend amplitude:
Vult men dit in in de vergelijkingen en deelt men cos(ωt) weg, dan bekomt men:
Dit is een stelsel van 2 vergelijkingen in de onbekende A1 en A2. Daar het rechterlid 0 is, moet de determinant 0 zijn om een oplossing verschillend van 0 te hebben:
Men vindt als oplossingen voor ω2:
Dit systeem heeft dus 2 natuurlijke trillingsmodes met de 2 natuurlijke frequenties:
Substitueert men de eerste oplossing terug in het stelsel voor da amplitudes, dan krijgt men dat A1 = A2. Beide massa's bewegen in fase. Beide massa' bewegen samen naar links of naar rechts. Met de tweede wortel bekomt men dat A1 = -A2. Beide massa's bewegen in tegenfase en sneller, want de inwerkende krachten zijn nu groter. Als de ene massa naar rechts beweegt, beweegt de andere naar links.
Algemene aanpak
[bewerken]Meer algemeen kan men de vergelijkingen in een matrix vorm gieten:
Volledig algemeen kan men dit opschrijven als::
De eerste matrix noemt men de traagheidsmatrix, de tweede de stijfheidsmatrix. Beide zijn symmetrische matrices. Als er demping aanwezig is, wordt een dempingsmatrix x de snelheden toegevoegd, maar dan wordt de oplossing via matrixrekenen veel moeilijker.
In een algemene benadering zal men deze matrices opstellen door te vertrekken van de vergelijkingen van Lagrange, of toch minstens van de kinetische energie T en de potentiële energie V. Dan worden de elementen van de traagheidsmatrix gehaald uit de kinetische energie:
De elementen van de stijfheidsmatrix worden dan gehaald uit de potentiële energie:
Daar beide matrices symmetrische matrices zijn, is het voldoende om de elementen van de diagonaal en een boven- of benedendriehoek uit te rekenen. Op deze manier kunnen ook systemen als een dubbele of driedubbele slinger eenvoudig behandeld worden.
Voor het voorbeeld hierboven krijgt men bv.
-
-
Men kan gemakkelijk zien dat dit tot de bovenstaande matrices zal leiden.
Onderstelt men een oplossing van de vorm |x|=|A|.eiωt, met|A| de vector van de amplitudes van de verschillende verplaatsingen, dan krijgt men na substitutie het stelsel:
Indien alle massa's dezelfde zijn (zoals in het voorbeeld hierboven) dan herleidt de traagheidsmatrix zich tot een factor m:
Dit is duidelijk een eigenwaardeprobleem in mω2. (Voor het begrip eigenwaarde, zie ook Voorwerpendynamica-2:Het diagonaliseren van de traagheidstensor) In het algemene geval zal men het probleem herleiden tot een eigenwaardeprobleem door links te vermenigvuldigen met M-1:
Bij het voorbeeld werd de vergelijking voor ω2 algebraisch opgelost. Voor matrices van een hogere orde zal men beroep doen op numerieke procedures om de inverse van de traagheidsmatrix, het matrixproduct en de eigenwaarden van dat product te berekenen.
De trillingsmodes die bij de eigenwaarden horen, noemt men de normale trillingsmodes. Men kan aantonen dat deze normale trillingsmodes een basis vormen in de ruimte van de verplaatsingen. Alle mogelijke trillingen van een systeem kunnen dus beschreven worden als lineaire combinaties van deze normale trillingsmodes.
Verdere behandeling hiervan kan men vinden bij Vibration: Multiple degrees of freedom systems and mode shapes of in teksten over lineaire algebra. Een grondige wiskundige bespreking kan men vinden in [goldstein]
Op het web zijn een verscheiden voorbeelden te vinden van systemen die in verschillende modes trillen. Op de link die hierboven gegeven werd toont men een ingeklemde staaf die op 6 verschillende manieren kan trillen. Een mooie verzameling van allerhande trillende voorwerpen, ketting, koord, membraan, baseballknuppel, bierflesje, guitar, kan men vinden op de site van Dan Russell, Kettering University: http://paws.kettering.edu/~drussell/demos.html. Zie onder "Vibrational Modes of Continuous Systems". Zie op dezelfde site ook naar de 3 modes van slingeren van een ketting van paperclips (http://paws.kettering.edu/~drussell/Demos/HangChain/HangChain.html) of de dynamisch absorber (http://paws.kettering.edu/~drussell/Demos/absorber/DynamicAbsorber.html)
Tenslotte moet hier misschien ook nog het eigenaardige gedrag van zwak gekoopelde oscillatoren vermeld worden, zoals kort besproken in Lagrange: Gekoppelde slingers.
Afleidingen
[bewerken]Er rest nog de afleidingen te geven voor de amplitude en de fasehoek bij een gedwongen trilling. Men kan dit op 2 manieren aanpakken. De eerste manier onderstelt dat de stabiele, particuliere oplossing van de vorm is. Men substitueert deze oplossing in de differentiaalvergelijking en leidt daaruit dan de uitdrukkingen voor A en φ af. De tweede, meer wiskundige aanpak, schakelt over op complexe getallen.
Eerste afleiding
[bewerken]Hierbij substitueert men de oplossing in de differentiaalvergelijking. Men bekomt dan:
of, met :
Schakelt men over op de dempingscoëfficiënt ζ dan krijgt men:
Men beschouwt nu 2 speciale waarden van de hoek:
- . Op dat ogenblik is en . Men krijgt:
- Neemt men de stand waarbij , dan krijgt men:
Op deze manier heeft men 2 vergelijkingen in de onbekende A een φ. Men verwijdert φ door beide vergelijkingen te kwadrateren en op te tellen:
Door beide vergelijkingen lid aan lid te delen, krijgt men de uitdrukking voor φ:
Als men teller en noemer deelt door ωn2 bekomt men de hoger gegeven formule. Bij de uitdrukking voor A kan men beide leden delen door ωn2
Tweede afleiding
[bewerken]Bij deze tweede afleiding doet men beroep op de complexe getallen. Men vervangt x in de vergelijking door z = x + iy en F.sinωt als Feiωt. Aan de vergelijking zal voldaan zijn als de reële delen van beide leden gelijk zijn en als de imaginaire delen gelijk zijn. Invullen in de differentiaalvergelijking levert:
Men schrijft nu z als A.ei(ωt - φ) en vult dit in en werkt uit. Men krijgt:
Het reëel deel hiervan is:
Het imaginair deel is:
Hiermede heeft men hetzelfde stelsel van 2 vergelijkingen in 2 onbekenden zoals hierboven en volgt men verder dezelfde weg.
Continue media
[bewerken]Bij een snaar van een piano of guitaar kan men niet meer spreken over afzonderlijke massa's die verbonden zijn door veren. Men heeft dan een continue massaverdeling en de matrixaanpak moet vervangen worden door een differentiaalvergelijking. Typisch voor deze is dat ze bestaat uit een combinatie van een partiële afgeleide naar de tijd en een partiële afgeleide naar de positie. Het is dus een totaal ander type van differentiaalvergelijking dan hierboven. Voor een snaar is het:
Bij golven in een continu medium onderscheidt men lopende en staande golven. Bij lopende golven verschuift het golfpatroon over het medium, bij staande golven blijft het patroon ter plaatse. Een lopende golf kan men gemakkelijk opwekken in een gespannen touw waarop men een korte slag geeft. Men krijgt dan een fenomeen als in de animatie hierbij.

Deze golven beantwoorden aan een functie van de vorm y=f(x-vt), waarbij de voortplantingssnelheid gegeven wordt door
met T = de spanning en m = de massa per lengte-eenheid (totale massa/lengte).
Aan een vast eindpunt treedt een reflectie op waarbij de fase van de golf omgekeerd wordt. Bij een vrij uiteinde treedt ook een reflectie op zonder faseomkering. En ook bij elke overgang naar een medium met een andere massa/meter treedt een gedeeltelijke reflectie op Dit alles is aanschouwelijk gemaakt op de site van Dan Russell, Kettering University, http://paws.kettering.edu/~drussell/Demos/reflect/reflect.html
Wanneer er meer golven zijn, dan ontstaat een interactie tussen de originele en de weerkaatste golven. Dit kan leiden tot staande golven. De plaatsen waar er geen verplaatsing is van het medium, de knopen, en de plaatsen met maximale uitwijking, de buiken, blijven dan ter plaatse.

De beweging wordt dan beschreven door een functie die bestaat uit het product van een functie van de plaats met een functie van de tijd. Als beide eindpunten vast zijn, moet er aan beide eindpunt een knoop liggen. Dit beperkt het aantal mogelijke oplossingen. Voor een harmonische vervorming blijft alleen een sinusfunctie over, want alleen die wordt sin(0)=0. Daar verder ook moet gelden dat sin(l)=0 is, moet l= nπ. Dit leidt tot een oplossing van de vorm:
met
De functie tussen de rechte haken bepaalt hoe snel de buiken op en neer bewegen, de functie ervoor hoeveel er zijn en hoe hoog (of breed) de beweging is
De waarde van de frequentie f = ω/2π horend bij n=1 noemt men de grondfrequentie, de andere de boventonen of harmonischen. In bijgaande figuur worden de uiterste standen getekend.
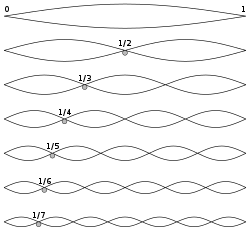
In de praktijk zal de beweging van een snaar bepaald worden door een som van bewegingen van verschillende frequenties. Op het internet zijn vele applets te vinden met animaties van golven. Zoek met "vibrating string" of "standing waves".
Einde













![{\displaystyle \quad =A[\cos(\lambda t+\alpha )+i\sin(\lambda t+\alpha )]+B[\cos(\lambda t+\beta )-i\sin(\lambda t+\beta )]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f1a54e1ecf82b907ddabcbc5768f91c2e3eeb02)






















































![{\displaystyle {\begin{matrix}\tan \phi ={\dfrac {2\zeta (\omega /\omega _{n})}{1-(\omega /\omega _{n})^{2}}}&\quad A={\dfrac {F/k}{\sqrt {[1-(\omega /\omega _{n})^{2}]^{2}+[2\zeta (\omega /\omega _{n})]^{2}}}}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ed16a6d0a34a9e0886c0e8cc5a1ad1aa0d1834e)
























![{\displaystyle \omega ^{2}\left[M\right]\left|A\right|={\begin{bmatrix}K\end{bmatrix}}|A|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/044f432a62855f7467e6a45665ddc1774914e950)

![{\displaystyle \left[M\right]^{-1}\left[K\right]|A|=\omega ^{2}|A|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a30350bc147e91816a37f793557255f589cb0eab)










![{\displaystyle [(\omega _{n}^{2}-\omega ^{2})^{2}+(2\zeta \omega \omega _{n})^{2}]A^{2}=(F/m)^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ae96cf3c603549e978814d38df44d6a49e3edce)







![{\displaystyle y_{n}(x,t)=A\sin({\frac {n\pi }{l}}x)[C_{1}\sin(\omega _{n}t)+C_{2}\cos(\omega _{n}t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd8a148ddb779ae80c0be71960d24c265e31a203)
