Klassieke Mechanica/Kinematica-2
Bewegende referentiesystemen
[bewerken]Wanneer men in een rijdende wagen of trein zit, dan heeft men de indruk dat het landschap voorbij schuift. Wij weten dat de aarde rond de zon draait, maar wat we zien is een zon die rond de aarde draait. Dit zijn gevallen van waarnemingen die gebeuren vanuit een bewegend referentiesysteem. In veel gevallen moet men voor berekeningen echter werken met een beschrijving in een stilstaand referentiesysteem en zal men dus deze bewegingen moeten omrekenen. De beweging gezien vanuit een bewegend systeem noemt men ook wel relatieve bewegingen, die ten opzichte van een vast systeem absolute beweging. In een eerste deel zal gehandeld worden over de snelheden, in een tweede over de versnellingen.
Snelheden
[bewerken]De drie snelheden
[bewerken]Een eenvoudig geval van een samengestelde beweging is die van een bootje of zwemmer in stromende water. Wie ooit in een rivier gezwommen heeft, weet dat hij dan een beetje tegen de stroming in moet zwemmen om volgens een rechte lijn naar de overzijde te bewegen. Als men zich gewoon zou laten drijven dan zou men door de stroming meegesleept worden. De snelheid van de stroming wordt daarom de sleepsnelheid genoemd. De rechte lijn die men wil volgen t.o.v. de oevers is de baan in het vaste systeem of de absolute baan. De schuine richting waarin men moet zwemmen of varen is de richting van de baan t.o.v. het water of de relatieve baan. "Relatief" betekent in deze context: "t.o.v. het bewegende systeem".
Voor het eenvoudige geval van een bootje op een rivier kan men zeggen dat de snelheid van de boot t.o.v. de oevers gelijk is aan de vectoriële som van de snelheid van de boot t.o.v. het water + de snelheid van het water op de plaats waar de boot zich bevindt. De formele definities zijn:
absolute snelheid va = de snelheid volgens de baan in het vaste systeem relatieve snelheid vr = de snelheid volgens de baan in het bewegend systeem sleepsnelheid vs = de snelheid van het punt van het bewegend systeem waarop het beschouwde punt zich bevindt.
Hiermede krijgt men de formulering van de stelling:
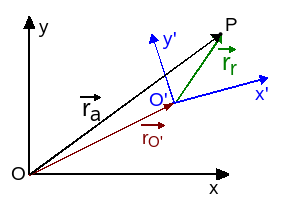
Om deze stelling te bewijzen moet men een vast referentiesysteem XYZ invoeren en een bewegend systeem X'Y'Z'. De positie van het punt P in het vaste systeem, de absolute positie, wordt dan gegeven door ra, en in het bewegend systeem, de relatieve positie, door rr. Er geldt volgend verband:
Hierbij kan men ra uitdrukken in functie van de eenheidsvectoren van het bewegend systeem:
Invoeren in vorige uitdrukking levert:
Om de verbanden tussen de snelheden te vinden moet men deze uitdrukking nu differentiëren naar de tijd. Men bekomt dan:
Men kan hierin verschillende termen onderscheiden:
- is de absolute snelheid
- is de snelheid van het punt p t.o.v. het bewegend assenkruis. Dit is de relatieve snelheid. Ze wordt gevormd door de verandering van de coördinaten van het punt binnen het bewegend assenkruis.
De resterende termen vormen de sleepsnelheid. Men kan hierin 2 bijdragen onderscheiden:
- is de translatiecomponent van de sleepsnelheid: vs,tr. Deze term treedt op zodra de oorsprong van het bewegend assenkruis beweegt en is voor alle punten binnen het bewegend systeem dezelfde, onafhankelijk van hun relatieve positie.
- : dit is een term die ontstaat als de eenheidsvectoren van het bewegend systeem veranderen t.o.v. het vaste systeem. Deze verandering kan alleen een richtingsverandering zijn. Dat betekent dat het bewegend systeem een rotatie uitvoert rond zijn oorsprong. Het is de rotatiecomponent van de sleepsnelheid: vs,rot. In de praktijk zal men de formule van de cirkelbeweging toepassen en zeggen dat deze component van de sleepsnelheid loodrecht zal staan op rr, in grootte gelijk zal zijn aan rrωassen en een zin zal hebben volgens de zin van ωassen.
Voor het eerst komt hier het verschil tussen een translatie en een rotatie ter sprake. Een translatie is een beweging waarbij alle punten van een voorwerp vectorieel dezelfde verplaatsing ondergaan. Het gevolg hiervan is dat ook de afgeleiden van deze verplaatsingsvector, de snelheid en de versnelling, voor alle punten van het voorwerp vectorieel dezelfde zijn. Het is zeer belangrijk dat men beseft dat een translerend voorwerp of assenkruis niet noodzakelijk volgens een rechte lijn moet bewegen. De definitie vergelijkt 2 posities, maar zegt niets over de weg die gevolgd werd om van de ene positie naar de andere te gaan. Transleren betekent ook dat richting behouden blijft: wat verticaal is blijft verticaal, wat horizontaal is blijft horizontaal. De cabientjes van een reuzenrad beschrijven een translatie alhoewel ze volgens een cirkel bewegen. De vloer blijft immers altijd horizontaal, de wanden verticaal. Elk punt beschrijft een zelfde cirkel, maar de cirkelbaan van een bepaald punt is verschoven t.o.v. de cirkelbanen van elk ander punt.

Bij een rotatie hebben alle punten een vectorieel andere snelheid en wordt richting niet behouden. Er is ook een punt met snelheid 0. Dit punt kan een vast punt zijn, maar kan ook veranderen in de loop van de tijd. In dat geval zal de snelheid van het punt wel nul zijn, maar het punt zal toch een versnelling hebben. Men noemt het dan het ogenblikkelijk rotatiecentrum (in België) of de momentane pool (in Nederland). Dit wordt in volgend hoofdstuk grondiger besproken. Een punt kan niet roteren. Alleen iets met een zekere uitgebreidheid kan roteren want men heeft minstens 2 punten nodig om een richting te definiëren.
Op het einde van de bespreking van de eendimensionale rotatie van voorwerpen wordt in de paragraaf "Rotatie versus translatie" een proef vermeld die aantoont dat rotatie en translatie zeer verschillende bewegingen zijn.
Voor de praktijk zal men moeten proberen om zo veel mogelijk informatie over elke van deze snelheden te verzamelen los van de andere. Het invoeren in de vergelijking moet dan toelaten om de ontbrekende verbanden te vinden. Bij een tweedimensionaal systeem kan men dus maximum 2 onbekenden hebben bij het invullen in de basisvergelijking.
Als men op basis van een statische tekening iets wil vertellen over snelheden, dan moet men zich laten leiden door de stelling dat een snelheid altijd rakend is aan de baan(cfr. het begin van dit hoofdstuk). Om de baan binnen het bewegend systeem te vinden moet men niet op zijn verbeelding steunen maar op geometrische eigenschappen zodat men zeker is van zijn besluiten. Men zal zich moeten laten leiden door het type verbinding tussen het punt en het bewegend systeem.
- Bestaat die verbinding uit een staaf, dan moet men proberen een bewegend assenkruis in te voeren zodat het andere einde van de staaf stilstaat in dat assenkruis (dat hoeft niet in de oorsprong te zijn). Dan zal het bewegende punt in het bewegend assenkruis een cirkel moeten beschrijven rond dat andere eindpunt.
- Als het bewegend punt op een of andere manier verplicht wordt langs iets ander te glijden (pin in een gleuf, mof over een staaf, langs een oppervlak), dan moet men proberen een bewegend assenkruis in te voeren zodat het element waarlangs het punt moet glijden stilstaat in dat bewegend assenkruis.
Over het bewegend assenkruis dat men gekozen heeft moet men 2 vragen stellen:
- Beweegt de oorsprong? Zo ja dan treedt de snelheid van die oorsprong op als sleepsnelheid voor alle punten binnen het bewegend systeem.
- Verandert de richting van de assen? Zo ja dan zit er een rotatiecomponent in de sleepsnelheid. vs,rot men zal bepalen met de formule van de cirkelbeweging.
Het is zelden nodig het vaste assenkruis goed te definiëren omdat men hier met snelheden bezig is. Men zal dat vaste assenkruis alleen moeten definiëren als men ook posities binnen dat vaste assenkruis nodig heeft. Zie in dit verband ook wat gezegd is in het hoofdstuk Basisbegrippen in de slotopmerkingen.
Voorbeelden
[bewerken]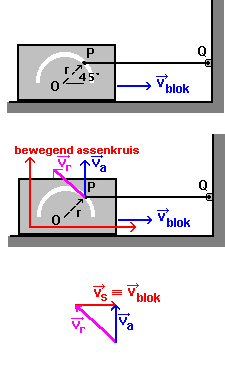
Als eerste eenvoudig voorbeeld kan men het geval beschouwen van een pin die in een gleuf in een blok moet glijden. Het blok schuift op het geven ogenblik naar rechts met een gegeven snelheid vblok. De pin zit op het einde van een staaf die scharnierend verbonden is met het vaste systeem in O. Men vraagt de hoeksnelheid van de staaf op het gegeven ogenblik.
- - De staaf OP vormt de verbinding van P met het vaste systeem. Binnen het vaste systeem beschrijft de pin dus een cirkel rond O. Op het gegeven ogenblik moet de pin omhoog bewegen. De absolute snelheid zal dus loodrecht staan op de staaf OP en va=OP.ωstaaf
- - De pin moet in de gleuf blijven. Die gleuf beweegt. De gleuf kan de baan van de relatieve snelheid worden als men een assenkruis kan invoeren zodat die gleuf stilstaat binnen dat assenkruis. De oplossing is eenvoudig: elk assenkruis verbonden met het blok is goed. De snelheid in de gleuf wordt zo de vr.
- - Het assenkruis beweegt mee met het blok: de oorsprong beweegt, de richting van de assen blijft onveranderd. Het is dus een zuiver translerend assenkruis en vs=vblok.
Zo bekomt men de snelhedendriehoek, waarin alleen de grootte van va en vr onbekend zijn. Het probleem is dus oplosbaar.
Hierna twee voorbeelden waarbij men zowel een translerend als een roterend assenkruis kan gebruiken. Bij een translerend assenkruis blijft de richting van de assen behouden. Daarom wordt het hier verticaal-horizontaal getekend. De oorsprong beweegt op een cirkel. Bij gebruik van een roterend assenkruis wordt het verbonden met de roterende staaf. Men probeert de oorsprong in een stilstaand punt te kiezen zodat de sleepsnelheid maar één component heeft, namelijk de rotatiecomponent. Om die uit te rekenen moet de relatieve positievector gekend zijn.

Men onderstelt telkens de hoeksnelheid van de eerste staaf en de geometrie van de opstelling bekend. Bemerk dat men bij de laatste uitwerking niet goed weet of de relatieve snelheid naar boven of naar onder zal gericht zijn. Ze blijkt uiteindelijk 0 te zijn. De snelhedendriehoek is ontaard tot 2 samenvallende zijden en va blijkt gelijk aan vs.
Een complexer voorbeeld
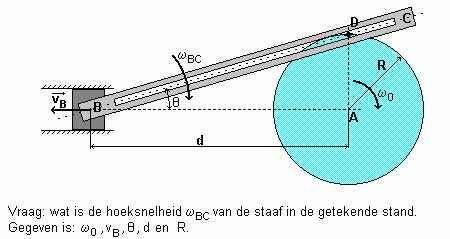
De analyse van de verbindingen leert dat de pin D enerzijds deel uitmaakt van de schijf en anderzijds verplicht wordt in de gleuf BC te glijden.
- Als vastgemaakt op de schijf moet D een cirkel rond A beschrijven in het vaste assenkruis. va zal dus horizontaal en naar rechts zijn.
- De gleuf is een bewegend element. Voor men de gleuf als de baan van de relatieve snelheid kan gebruiken, moet men een assenkruis invoeren zodat de gleuf stil staat binnen dat assenkruis. De gleuf roteert, maar niet rond een vast punt. Men kent wel de snelheid van het punt B. Men zal dus een assenkruis moeten invoeren dat roteert met de staaf en transleert met B. Men kiest dus B als oorsprong. Voor vs krijgt men 2 componenten:
- - een translatiecomponent = vB
- - een rotatiecomponent = BD.ωBC, loodrecht op de staaf BC en naar beneden (waarschijnlijk).
- Met het gekozen assenkruis wordt de gleuf BC de baan van D binnen het bewegend assenkruis. vr zal voor de gegeven situatie naar rechts gericht zijn volgens de gleuf.
Dit levert de volgende situatie:

Daar men hier met meer dan 3 vectoren te doen heeft zal men de vergelijking projecteren. De gevraagde ωBC zit in de vs,rot, die volgens de y-as van het bewegend assenkruis ligt. Projectie op die as levert een vergelijking waarin alleen vs,rot als onbekende voorkomt, zodat men daaruit onmiddellijk ωBC kan berekenen.
Met BD=d/cos θ:
Tot slot: bij de voorbeelden hierboven gaat het telkens over drie elementen: een bewegend punt, een bewegend systeem en een vast systeem. Meer kan men in één toepassing van de stelling van de drie snelheden niet gebruiken. De werkelijkheid is echter dikwijls complexer. Men kan een bewegend systeem hebben dat zelf beweegt t.o.v. een ander bewegend systeem. Men kan een punt hebben met twee verbindingen naar bewegende systemen i.p.v. naar een bewegend en naar een vast systeem. In al die gevallen zal men meerdere keren drie elementen moeten kiezen, een bewegend punt, een bewegend systeem en een "vast"systeem", zodat men de stelling van de drie snelheden kan formuleren. Men zal de theorie meerdere malen moeten toepassen.
Een trainingsprogramma
[bewerken]De moeilijkheid met dit soort probleem bestaat enerzijds uit het feit dat men over snelheden moet spreken terwijl men op een statische tekening kijkt en anderzijds dat de helft van wat men nodig heeft om deze problemen op te lossen bestaat uit algemene (meetkundige) kennis. Er werd een interactief programma ontwikkeld om deze elementen van algemene kennis wat duidelijker aan te geven. Het dateert nog van de tijd van de VGA-schermen met een resolutie van 640x480 pixels (ooit vond men dat een enorme vooruitgang!) maar is nog perfect bruikbaar. Men kan het hier vinden als een zip-bestand. Liefst in een afzonderlijke folder uitpakken, eventueel met XP-compatibiliteit uitvoeren.
Versnellingen
[bewerken]Een woord vooraf
[bewerken]Intuïtief heeft men nog enig zicht op snelheden. Men kan bv. gemakkelijk begrijpen dat bij een staaf die een willekeurige beweging uitvoert, de snelheidscomponenten van beide uiteinden volgens de richting van de staaf dezelfde moeten zijn, want anders zou de staaf korter of langer worden. Dezelfde redenering geldt absoluut niet op het niveau versnelling. Als een draaiende staaf aan één einde vastzit aan een as, dan heeft dat einde geen versnelling terwijl het andere einde minstens een normale versnelling heeft, die naar die as gericht is. Wanneer men te maken heeft met versnellingen geldt als regel: houd u aan de formules, reken niet op intuïtie.
De wet van Newton legt een verband tussen krachten en versnellingen. Als men geen intuïtief zicht heeft op versnellingen betekent dat dus ook dat men geen intuïtief zicht heeft op de krachten die optreden in dynamische situaties: versnellen, vertragen, een bocht nemen, trillende systemen, enz.
Een nieuwe operator
[bewerken]Als men een vector beschrijft enerzijds met coördinaten in een vast assenkruis en anderzijds met coördinaten in een roterend assenkruis (relatieve coördinaten), dan zal men bij de afgeleide naar de tijd van de relatieve coördinaten nog een sleepsnelheid moeten bijtellen om de afgeleide in het vaste systeem te bekomen. Deze sleepsnelheid is gegeven door een cirkelbeweging van het punt rond de rotatie as. Deze snelheid kan men in het algemeen uitdrukken met een vectorieel product als . Dit verband werd hierboven afgeleid voor een positievector, maar is onafhankelijk van de aard van de vector. In het algemeen zou men dus over een sleepverandering kunnen spreken als het verschil tussen de absolute en de relatieve afgeleide. Dit verband kan zeer dikwijls toegepast worden en wordt daarom geformuleerd in de vorm van een operator om te differentiëren in een roterend assenkruis:
Hierin duidt "relatief" op een bewerking die uit te voeren is op vectoren bepaald t.o.v. het bewegend systeem.
Met deze operator wordt de vorige afleiding een stuk korter:
Hierin is alleen rr gedefinieerd in een (eventueel) roterend assenkruis. Voor het differentiëren moet alleen voor deze term de operator toegepast worden:
De versnelling
[bewerken]Men kan nu ook verder gaan naar de versnelling. Door differentiëren van de uitdrukking voor va hierboven, bekomt men de absolute versnelling. Hierbij zijn rr en vr gedefinieerd in een (eventueel) roterend assenkruis. De haakjes groeperen termen die afkomstig zijn van het differentiëren van een zelfde term:
Men kan deze termen op verschillende wijze groeperen. Een mogelijkheid is weer volgens sleep- en relatieve versnelling en dan blijkt er nog een term bij te komen:
De sleepversnelling, d.i. de versnelling van het punt van het bewegend systeem waarop het beschouwde punt zich bevindt, bestaat uit 3 termen:
- de versnelling van de oorsprong van het assenkruis; Dit kan men de translatiecomponent van de sleepversnelling noemen.
- de factor tussen de haken levert de sleepsnelheid, die loodrecht staat op ω. Het volgende vectoriële product levert een vector die loodrecht staat op het vlak van vs en ω. Het is een vector die naar ω gericht is, nl. de normale component van de sleepversnelling. Grootte = ω2.rr.sinθ, met θ de hoek tussen rr en ω.
- : dit is de tangentiële component van de sleepversnelling.
Naast de relatieve versnelling is er dan nog de term . Deze term verscheen reeds bij de studie van de versnelling in poolcoördinaten in het eerste deel van Kinematica en werd er verklaard in de paragraaf "De term 2.vr.ω" . Zoals daar kan men ook hier vaststellen dat de term eenmaal afkomstig is van de sleepverandering van vr (d.i. een richtingsverandering) en eenmaal van de verandering van de grootte van rr. Alleen wanneer vr evenwijdig is aan ω bestaat deze term niet. Spijtig genoeg is er geen volledige unanimiteit over de benaming van de term. Deze term geeft de versnelling zoals gezien in het vaste assenkruis. Voor sommigen is dit de coriolisversnelling, maar anderen reserveren die term voor de versnelling die men ziet in het bewegend assenkruis en die heeft de tegengestelde zin (zie volgende punt). Deze laatste groep noemt dit dan de complementaire versnelling. Het blijkt in elke geval nog eens dat de versnelling componenten bevat waaraan intuïtief niet gedacht wordt, alhoewel men ze nadien wel kan verklaren.
Voorbeeld Het is interessant om te zien hoe men via verschillende benaderingen uiteindelijk op dezelfde termen kan uitkomen, alhoewel langs ogenschijnlijk totaal verschillende wegen. Zij bv. een draaiend plateau gegeven met straal R en hoeksnelheid ω. Op de rand van dit plateau loopt iemand met relatieve snelheid vr tegen de rotatie van het plateau in. Men vraagt de versnelling van die persoon te berekenen.
Eerste benadering. Als de persoon stilstaat, dan beschrijft hij een cirkel met hoeksnelheid ω. Zijn beweging t.o.v. de schijf kan beschouwd worden als een relatieve cirkelbeweging met hoeksnelheid ωr = vr/R. Men kan dus zeggen dat hij t.o.v. het vaste systeem een cirkel beschrijft met hoeksnelheid ω-ωr. Hierbij hoort een normale versnelling met grootte
Deze normale versnelling is naar binnen, naar de as gericht.
Tweede benadering. Men beschouwt de beweging binnen een assenkruis roterend met de schijf. Men krijgt dan voor de drie componenten van de absolute versnelling:
- , naar binnen gericht
- , naar binnen gericht
- . Deze term is naar buiten gericht.
Men bekomt dus exact dezelfde termen, maar onder andere benamingen.
Eenvoudiger formule voor onvervormbare voorwerpen
Binnen onvervormbare of starre voorwerpen stelt zich regelmatig het probleem om de versnelling van een punt te berekenen uitgaande van de bekende versnelling van een ander punt. Voor deze toepassing kan bovenstaande formule sterk vereenvoudigd worden. Zij punt A het referentiepunt met een bekende versnelling en punt B het punt waarvan men de versnelling wil berekenen. Men kan dan een translerend assenkruis verbinden met A en vandaar kijken naar B. Daar het een translerend assenkruis is, valt alvast de coriolisversnelling weg. De versnelling van B is dus alleen de som van de versnelling van A met een relatieve versnelling van B t.o.v. A. Als het over een onvervormbaar voorwerp gaat, dan kan die relatieve beweging alleen een rotatie zijn met een hoeksnelheid ω en/of een hoekversnelling α. Als er een hoeksnelheid is, dan is er ook een normale versnelling van B naar A met grootte AB.ω2. Als er een hoekversnelling is, dan is er een tangentiële versnelling loodrecht op de rechte AB, met een zin volgens de zin van α en met grootte AB.α . Samengevat:
Coriolisversnelling en bewegingen op aarde
[bewerken]Normaal wordt de aarde als een vast systeem beschouwd, maar dat is ze in feite niet. Dat heeft gevolgen voor vele bewegingen op aarde. Hier moet even vooruit gelopen worden op het volgend hoofdstuk, waarin de wet van Newton behandeld wordt. Deze wet stelt dat de som van alle krachten op een massa steeds gelijk zal zijn aan het product van die massa maal de versnelling van die massa. Als er geen krachten op een massa uitgeoefend worden, dan is er geen versnelling, d.i. de massa blijft in rust of blijft met constante lineaire snelheid bewegen. Deze wet mag enkel toegepast worden in een systeem dat in rust is of dat met constante snelheid beweegt. In een roterend systeem schijnt de wet niet te kloppen. De versnelling die een waarnemer ziet, berekend op basis van de baan in het bewegend systeem, is de relatieve versnelling. Als alle uitwendige krachten = 0 zijn dan blijkt er in een roterend assenkruis toch nog een relatieve versnelling op te treden. Wiskundig betekent het dat er in de relatieve versnelling, de versnelling gezien door de waarnemer in het bewegend systeem, termen moeten komen die juist het tegengestelde zijn van de sleepversnelling en de complementaire versnelling zodat de totale som 0 is. De man in het bewegend systeem kent dus aan het punt een versnelling -2*vr*ω toe. Het is deze versnelling, zoals waargenomen door de waarnemer in het bewegend systeem, die meestal de coriolisversnelling genoemd wordt.

Dat vrij bewegende objecten een gekromde baan volgen binnen een roterend assenkruis, kan ook gemakkelijk begrepen worden m.b.v. de figuur hiernaast. Onderstel dat een iemand in punt A staat op een linksom draaiende schijf en een bal wil werpen naar een persoon in B, aan de buitenkant van de schijf. Wanner de man in A de bal gooit, geeft hij aan die bal een relatieve snelheid in de richting van B, radiaal naar buiten. Als we de luchtweerstand even verwaarlozen, dan blijft de horizontale component hiervan constant. Als hij de bal gooit vanuit het centrum van de schijf, dan heeft hij daar geen sleepsnelheid t.o.v. de grond. Naarmate de bal zich verwijdert van A, passeert hij over punten met een steeds grotere omtreksnelheid, die de sleepsnelheid is. De bal blijft dus meer en meer achter op de lijn AB. Voor de waarnemer op de schijf buigt zijn baan naar rechts af. Men kan die richtingsverandering van de relatieve snelheid ook afleiden uit de vectoriële formule . Als va constant moet blijven maar -vs neemt toe, dan moet vr zich aanpassen door meer naar rechts te wijzen.
De waarnemer in een bewegend systeem ziet dat alle massa's de neiging hebben om naar buiten te bewegen en dat hun banen op een speciale manier afgebogen worden. Hij kan dit verklaren door aan te nemen dat hij in een systeem leeft waarin op alle massa's een naar buiten gerichte kracht werkt, de middelpuntvliedende kracht, en een speciale dwarskracht die alle banen doet afwijken. Dit is een verklaring door het aannemen van traagheidskrachten of pseudokrachten. Deze krachten komen immers niet van andere voorwerpen maar zijn eerder een wiskundige compensatie om de wet van Newton toch te kunnen opschrijven in een roterend assenkruis. In een inertiaalstelsel moet men opschrijven:
Het invoeren van een middelpuntvliedende kracht en een corioliskracht komt er wiskundig op neer dat men de termen m(as + acomp), die de dimensie hebben van een kracht, naar het linkerlid overbrengt en die dan als een echte kracht gaat interpreteren. Deze interpretatie komt meer overeen met onze ervaring. Wanneer een auto met een hoge snelheid een bocht neemt, dan voelen we ons naar buiten gedrukt. Ook behoren krachten meer tot ieders begrippenkader dan versnelling. Een uitleg in termen van pseudokrachten is daardoor begrijpelijker dan een beschrijving vanuit een inertiaalstelsel.
De hoeksnelheid van de aarde is vrij klein: 2π radialen in 24 u of 7,27.10-5 rad/s. De bijhorende middelpuntvliedende kracht is dan ook klein en wordt in de praktijk verrekend in een iets kleinere waarde van g aan de evenaar dan aan de polen.

De coriolisversnelling levert de verklaring voor de draaiende luchtmassa's rond hoge- of lagedrukgebieden. Vanuit een hogedrukgebied stromen de winden naar buiten. Zodra ze echter in beweging komen begint de coriolisversnelling te spelen. Die blijft spelen zolang er een vr is. Volgens de conventie van de rechtsdraaiende schroef ziet men dat die versnelling volgens de blauwe pijlen gericht is. De winden worden dus gedwongen te cirkelen in wijzerzin. Volgens de vroegere Vlaamse weerman Armand Pien, kan men de draaizin hiervan gemakkelijk onthouden door te formuleren dat, in ons noordelijk halfrond, de winden rond een Hoge drukgebied draaien in de zin van een Horloge. Bij een lagedrukgebied stromen de winden naar binnen. Daardoor ontstaat een werveling in tegenwijzerzin.
Voor bewegingen op het aardoppervlak betekent dit dat de coriolisversnelling voor een beweging volgens de evenaar, loodrecht staat op het aardoppervlak. Bij een beweging naar het oosten zal een voorwerp iets opgelicht worden, bij een beweging naar het westen iets neergedrukt worden. Dit staat bekend als het Eötvös effect. Bij een Noord-Zuid verplaatsing is acor =0 omdat vr dan evenwijdig is met ω.
Bij bewegingen rond de polen ligt de coriolisversnelling ongeveer evenwijdig met het aardoppervlak. Bij de polen is het effect dus het sterkst.
Als men te maken heeft met een verplaatsing in een horizontaal vlak en men is alleen geïnteresseerd in de de component van de coriolisversnelling in dat vlak, dan kan men die bekomen door te rekenen met de component van ω loodrecht op dat vlak. (Het is een eigenschap van het vectorieel product dat het resultaat in een bepaald richting alleen bepaald wordt door de orthogonale projecties van de argumenten op een vlak loodrecht op die richting.) Dit levert qua grootte:
- met φ de breedtegraad waarop dit horizontale vlak zich bevindt.
Voor de polen is φ = 90° en sin φ dus 1, voor de evenaar is φ = 0 en sin φ = 0. Dit geldt nu echter voor alle richtingen van een snelheid op de evenaar.
Ook bij een schot over een grote afstand moet men rekening houden met deze coriolisversnelling. Dat het water bij het uitlopen van het bad ook door deze coriolisversnelling begint te draaien kan, maar er zijn veel andere invloeden die sterker kunnen zijn, zoals bv. verontreinigingen op de bodem van de badkuip of op het roostertje.
Bolcoördinaten
[bewerken]In een vlak kan men de positie van een punt eenduidig bepalen m.b.v. een afstand van een referentiepunt en een hoek t.o.v. een referentierichting. Zo bekomt men de poolcoördinaten. In de ruimte heeft men hiervoor een afstand en twee hoeken nodig. Een eerste hoek θ bepaalt de positie van het verticale vlak door de positievector. De tweede hoek φ bepaalt de positie van deze vector t.o.v. de verticale in dit vlak. Dit zijn de bolcoördinaten. Spijtig genoeg zijn de benamingen van deze hoeken niet eenduidig vastgelegd. Naast verschillende namen zijn er ook verschillende definities in voege, zodat men bij gebruik van formules uit verschillende werken moet uitkijken naar wat met wat overeenkomt.

Men kan nu een orthonormaal assenkruis definiëren in het beschouwde punt door eenheidsvectoren in te voeren die in het gegeven punt raken aan de parameterkrommen door dat punt, die men bekomt door telkens één parameter te laten variëren en de andere constant te houden. Men bekomt zo de eenheidsvectoren ur, uφ, uθ. In deze volgorde vormen ze een rechtsdraaiend rechthoekig assenkruis.
Om de snelheid en versnelling te berekenen in bolcoördinaten kan men vertrekken van de formules die de transformatie geven naar cartesische coördinaten. De eerste hiervan is:
- x = r.sin φ.cos θ
Hierbij berekent men eerst de componenten vx, vy en vz in functie van r, φ en θ en hun afgeleiden. Dan projecteert men deze componenten op de assen van de bolcoördinaten om vr, vφ en vθ te bekomen. Dit levert echter zeer lange berekeningen op. Differentiëren van de uitdrukking hierboven levert immers 3 termen, nogmaals differentiëren levert 9 termen!
Een eerste kortere methode is opnieuw de operator voor differentiëren in een roterend systeem te gebruiken. Om de notatie eenvoudig te houden zal de notatie van Newton voor de afgeleiden naar de tijd gebruikt worden. Een eerste afgeleide wordt daarbij aangeduid door één punt, een tweede afgeleide door twee punten boven het symbool. wordt gelezen als "φ punt", als "φ dubbel".
De vector ω zal hier echter samengesteld zijn uit 2 rotaties:
- een verandering van φ leidt tot een rotatievector
- een verandering van θ levert een verticale rotatievector. In het assenkruis van de bolcoördinaten wordt dit
Men krijgt dan voor de snelheid:
De laatste term kan als volgt uitgerekend worden:
Samen levert dit als snelheidscomponenten:
of:
Men heeft , zodat men bovenstaande formule ook kan lezen als een manier om de afgeleiden van de eenheidsvectoren te berekenen. Men kan dus op analoge manier werken om de versnelling te berekenen als afgeleide van de snelheid. Alhoewel deze methode reeds 10x korter is dan via de cartesische coördinaten, is er nog een kortere methode.
Kortste methode
Wanneer een punt, bepaald door bolcoördinaten, beweegt, dan kan men die beweging ook beschouwen als opgebouwd uit de rotatie van het verticale vlak door de positievector r gecombineerd met een beweging binnen dat vlak. Binnen dat vlak komen de parameters r en φ dan overeen met de parameters van de poolcoördinaten. De snelheid en versnelling in poolcoördinaten is bekend en vrij eenvoudig. Voor de snelheid hoeft men er alleen een sleepsnelheid aan toe te voegen (in casu vθ) en voor de versnelling een sleepversnelling en een complementaire versnelling, die vrij eenvoudig te berekenen zijn. Alleen heet de hoek θ van de formules van de poolcoördinaten hier nu φ!
- De relatieve snelheid (genoteerd met subscript "rel" om verwarring met de radiale snelheid te vermijden):
- De relatieve versnelling:
- De sleepversnelling is een normale + een tangentiële versnelling. De normale versnelling ligt in een horizontaal vlak en heeft dus 2 componenten, de tangentiële ligt volgens uθ:
- Tenslotte de complementaire versnelling (alles wat nodig is, is hierboven gegeven):
Alles herschikken volgens de componenten van de bolcoördinaten levert:
Daarmee zijn deze vrij ingewikkelde formules gevonden.
Deze aanpak is ontleend aan het boek "Mécanique générale", 2e uitgave (1998), door Christian Gruber en Willy Benoit, professoren aan de Ecole polytechnique fédérale in Lausanne (EPFL), ISBN: 2-88074-305-2. Wie zowat alles wil weten over bolcoördinaten (Engels: spherical coordinates) kan terecht op deze pagina: http://mathworld.wolfram.com/SphericalCoordinates.html.
















































