Klassieke Mechanica/Equivalenties
Equivalente vectorsystemen
Inleiding
[bewerken]Dat de oorzaak van het gewicht van een voorwerp ligt in de aantrekkingskracht van de aarde, is een vertrouwd idee. Men weet ook dat men dat gewicht kan voorstellen als een kracht die aangrijpt in het zwaartepunt van het voorwerp. Dat is echter geen rechtstreekse weergave van de fysische situatie. In werkelijkheid werkt de aantrekkingskracht van de aarde op elk deeltje van een voorwerp. Die aantrekkingskracht creëert dus een verzameling van evenwijdige vectoren. Die verzameling vervangt men door een wiskundig equivalente beschrijving als men die voorstelt als één kracht aangrijpend in het zwaartepunt van het voorwerp.
Hier en in vele andere gevallen is het interessant om een complexe situatie van vectoren te kunnen vervangen door een eenvoudiger verzameling die echter voor alle berekeningen in de mechanica hetzelfde resultaat zal opleveren. Dit noemt men overgaan op een equivalent vectorsysteem. De bewerking is vooral bekend voor krachten. De theorie die hier behandeld wordt, zal men in veel boeken dan ook vinden onder de titel Samenstellen van krachten of Equivalente krachtensystemen. De theorie is echter veel breder toepasselijk, nl. op alle vectorsystemen waarbij men gebruik maakt van de som van die vectoren en van de som van hun momenten t.o.v. een punt of as. Zo een vectorsysteem is bv. ook impuls en impulsmoment.
Om de zaken concreet te houden, zal de theorie echter uitgewerkt worden aan de hand van krachten. Op het einde wordt op de andere toepassingen gewezen.
De verplaatsingsformule
[bewerken]Krachten vormen een voorbeeld van een verzameling vectoren waarbij de som van deze vectoren belangrijk is (in de wet van Newton of voor de translatie van het massacentrum) en waarbij ook de som van de momenten van deze vectoren t.o.v. een bepaald punt of een as een belang heeft (voor de rotatiebeweging). Als men het moment van een verzameling krachten berekend heeft t.o.v. een bepaald punt, en men heeft het later nodig t.o.v. een ander punt, dan kan men zich de vraag stellen of men van voorafaan moet herbeginnen of of men de berekeningen kan vereenvoudigen door uit te gaan van het vorige resultaat. Het antwoord hierop is positief en wordt gegeven door de verplaatsingsformule.

Onderstelt men een verzameling krachten Fi, waarvan men het moment berekent t.o.v. het punt O. Men heeft dan:
Als men nu het moment nodig heeft t.o.v. een ander punt P dan wordt dit:
Dit laatste is te schrijven als de verplaatsingsformule:
Hierin is rOP de positie van P t.o.v. O. -rOP is dan de positie van O t.o.v. P. Men kan deze formule dus lezen als:
- Het moment t.o.v. P = het moment t.o.v. O + het moment van de som van alle krachten
- geplaatst in O (oude positie) t.o.v. P (nieuwe positie)
Later wordt hieraan een interpretatie gegeven waarmee de formule eenvoudig te onthouden is.
Koppel van krachten
[bewerken]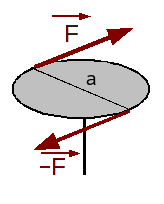
Een koppel van krachten is in de theoretische mechanica een stel van twee even grote maar tegengestelde krachten, die niet op één lijn liggen.
Zo'n koppel treedt bv. op als men iets probeert te verdraaien met beide handen. De loodrechte afstand tussen de twee dragers, a in de figuur, noemt men de koppelarm. Als men het moment berekent t.o.v. één van de twee aangrijpingspunten, dan is het duidelijk dat het moment van het koppel = a.F . De som van de krachten van een koppel is nul (een koppel veroorzaakt geen translatie). Wanneer men nu naar de verplaatsingsformule kijkt, dan blijkt dat het moment van een koppel niet zal veranderen, als men het berekent t.o.v. een ander punt. Besluit:
- Het moment van een koppel is onafhankelijk van het berekenings- of herleidingspunt.
Een concreet voorbeeld hiervan kan men ondervinden, als men een wiel van een auto moet vervangen. Als men de wagen opgekrikt heeft en het wiel niet geblokkeerd heeft m.b.v. de handrem of door een versnelling in te schakelen, zal men bij het proberen om de bouten los te draaien vaststellen dat het volledige wiel gaat draaien i.p.v. alleen de bout. Het maakt immers niet uit of het koppel mooi op de as uitgeoefend wordt of ergens anders op het wiel.
Vroeger zei men : "Het moment van een koppel is een vrije vector". Hiermede bedoelde men dat men de momentvector van een koppel mag 'verplaatsen' zonder dat men hiervoor een correctie moet invoeren. Omgekeerd kan men elk gegeven moment beschouwen als veroorzaakt door een koppel van krachten. Of nog: een koppel van krachten is de fysische realisatie van wat men wiskundig met alleen maar een momentvector beschrijft. Men moet leren krachten en momenten als grootheden met een eigen bestaansreden te beschouwen, net zoals snelheid- en impulsvectoren afzonderlijk grootheden zijn, of snelheid en kinetische energie. Of: er is een ruimte van krachten en een ruimte van momenten.
De equivalentierelatie
[bewerken]Voor verzamelingen van gegeven krachten en gegeven momenten definieert men nu de volgende equivalentie:
- twee systemen zijn equivalent als de som van alle krachten in beide systemen dezelfde is en als de som van de gegeven momenten en van de momenten van alle krachten t.o.v. elk punt van de ruimte dezelfde is.
Dit is een niet erg praktische definitie. Eén blik op de verplaatsingsformule leert dat men dit kan vereenvoudigen tot een definitie die hetzelfde betekent, maar wel te controleren is:
- Twee systemen zijn equivalent als in beide systemen de som van alle krachten dezelfde is en de som van alle gegeven momenten
- + de som van de momenten van alle krachten t.o.v. één punt van de ruimte dezelfde is.
De meest eenvoudige toepassing van deze equivalentierelatie en de oudst bekende is het verschuiven van een kracht over zijn drager. Hierbij blijft de som van beide systemen duidelijk dezelfde en ook het moment t.o.v. een willekeurig punt. Het moment van de kracht F t.o.v. een punt P wordt immers gegeven door het vectorieel product rP-F x F, met rP-F de positievector van het aangrijpingspunt van F t.o.v. P. Dit vectorieel product verandert niet bij het verschuiven van F (zie het vectorieel product in vorig hoofdstuk).
Tot midden vorige eeuw werd dikwijls als een postulaat gesteld dat men een kracht mag verschuiven over zijn drager. De notie van equivalentie was toen duidelijk nog niet goed uitgeklaard. Maar zelfs tot midden de jaren 80 van de vorige eeuw kon men hier en daar de affirmatie horen dat de vectoren in de fysica niet dezelfde zijn als de vectoren in de wiskunde. De fysica zou zogezegd met glijdende vectoren werken en de wiskunde met vrije vectoren. Dit gaat ook duidelijk terug op een slecht begrip van de equivalentie zoals hierboven gedefinieerd. Het is ook grote onzin, want het zou betekenen dat men in de fysica aan wiskunde doet die niet tot de wiskunde behoort.
De verplaatsingsformule kan men nu als volgt interpreteren. Als de som van de krachten inwerkt in O, dan hoort daarbij een moment μO. T.o.v. P heeft die som in O een moment. Als men die som laat aangrijpen in P, heeft die som geen moment meer t.o.v. P. Om te voldoen aan de equivalentierelatie moet men er dus het moment van die som in O t.o.v. P bijvoegen.
Een grafisch bewijs
[bewerken]
Vroeger werd de nood aan een bijkomend moment dikwijls aangetoond met dit eerder grafisch bewijs. Onderstel een kracht in een punt P. Men wil deze kracht verplaatsen naar het punt P' dat niet op de drager van die kracht ligt. Men kan dan in P' een kracht gelijk aan invoeren en het tegengestelde hiervan. Dit verandert niets aan de situatie want de som van deze 2 krachten is nul en ook hun moment is nul t.o.v. van elk punt. Men kan deze 3 vectoren nu echter anders uitlezen, nl. de vector kan men zien als de verplaatste vector . De 2 resterende vectoren (in het groen op de figuur) vormen dan een koppel met een moment dat overeenkomt met het moment van in de originele positie ten opzichte van de nieuwe positie.
De speciale gevallen
[bewerken]Wanneer men deze equivalentierelatie meerdere keren na elkaar toepast, blijkt dat de som van de krachten na de eerste toepassing kan voorgesteld worden door één kracht, de resultante R. Deze verandert verder niet meer. Alleen het moment verandert nog bij verandering van het herleidingspunt. Op basis van de verplaatsingsformule voor momenten zal dat nieuwe moment echter op een zeer eenvoudige manier kunnen berekend worden uit het vorige. Men kan dit als volgt voorstellen:
| Gegeven systeem | in oorsprong | in willekeurig punt P |
| (1) |
Men kan zich nu de vraag stellen of er zich speciale gevallen kunnen voordoen bij deze herleiding in bepaalde punten. Deze speciale gevallen zijn gemakkelijk te formuleren :
- herleiding tot een zuiver moment zonder resultante (R = 0). Het eenvoudigste geval hiervan is een koppel. Als dit het geval is, dan verandert het systeem niet bij overgang naar een ander herleidingspunt. Men drukt dit ook uit door te stellen dat het moment van een koppel onafhankelijk is van het herleidingspunt. De situatie kan echter ook voorkomen met meer dan twee vectoren, nl. telkens als de krachtvectoren een gesloten veelhoek vormen. Dit treedt bv. op bij een elektrische motor.
- herleiding tot een resultante zonder moment (of μP = 0). Dit noemt men ook wel : herleiding tot een zuivere resultante.
- alleen het moment zal verder veranderen bij verandering van het herleidingspunt. Als het vorige geval niet mogelijk is, kan men vragen naar een punt waar de momentvector minimaal is. Dit blijkt het punt te zijn waar de momentvector evenwijdig is met de resultante of de situatie van de schroefas. Men kan dit ook beschouwen als een herleiding tot de invarianten van het systeem.
Dat het moment van een koppel onafhankelijk is van het herleidingspunt, kan men in de praktijk ervaren als men de bouten van een autowiel wil losschroeven. Zelfs bij gebruik van een kruissleutel zal het wiel, als het niet geblokkeerd werd, rond zijn as beginnen draaien en men zal de bouten noch los, noch vast krijgen.
De laatste twee gevallen zijn speciale gevallen van de formule (1) en worden nu meer in detail bekeken.
Herleiding tot een zuivere resultante
[bewerken]De voorwaarde dat μP = 0 moet zijn, leidt tot de vergelijking:
- (2)
Een voorwaarde voor het bestaan van een oplossing is dat R loodrecht zou staan op μo. Dit kan toevallig zo zijn, maar er zijn twee systemen waarbij men bij voorbaat zeker is dat de aan deze voorwaarde voldaan is en die dus altijd tot één enkele resultante kunnen herleid worden. Deze twee systemen zijn:
- systemen van evenwijdige krachten
- vlakke krachtensystemen
- samenlopende krachten.
Systemen van evenwijdige krachten
[bewerken]Bij een systeem van evenwijdige krachten hebben alle krachten een zelfde richting. Het moment zal altijd loodrecht moeten staan op die richting, terwijl de resultante altijd volgens die richting moet liggen. Resultante en moment staan dus zeker loodrecht op elkaar.
Men kan nu gemakkelijk het punt berekenen waar men die resultante moet plaatsen. Men zoekt naar een punt Z met positievector zodat geldt:
Als men een eenheidsvector invoert volgens de gemeenschappelijke richting, dan krijgt men: en Invoeren in vorige uitdrukking levert:
- (3)
Een oplossing is:
Hierin zijn de Fi de projecties op de gemeenschappelijke richting, met het correcte teken! Het heeft geen belang wat men als positieve of negatieve zin kiest. De vectoriële formule zal natuurlijk volgens projecties op assen moeten uitgewerkt worden. Vectoren kunnen niet vervangen worden door een getal, wel de coördinaatprojecties:
Wanneer men met een continue krachtverdeling werkt, dan zal men met een integraal werken i.p.v. een som:
Hierin geeft de functie f(r) de projectie van de kracht als functie van de positie. Deze integraal kan ook over een oppervlak zijn i.p.v. over een volume. Dit is het geval zijn als men de resultante van de druk van het water tegen een dam of wand wil berekenen.
Een vergelijking die uitgaat van een vectorieel product, heeft echter geen punt als oplossing maar een rechte. Er is een onbepaaldheid in de richting van . Als men bij de berekende waarde een willekeurige component telt in de richting van , dan verandert dat niets aan de waarde van het rechterlid in vergelijking (3). Het vectorieel product van evenwijdige vectoren is immers nul. Dat is dus ook een oplossing. In de praktijk komt het erop neer dat de resultante, nadat ze in het gevonden punt geplaatst werd, mag verschoven worden over haar drager, d.i. volgens de richting van .
Voorbeeld

Aan een paal zijn drie touwen bevestigd, die eraan trekken zoals aangegeven op de figuur. Bereken de resultante en de positie ervan.
Oplossing
Men voert een assenkruis is zoals getekend. De x-as dient voor de projecties van de krachten, de y-as om de posities van de aangrijpingspunten te bepalen.
- Resultante: 50 - 20 + 30 = 60 kg
- Aangrijpingspunt: ((50x0,5) + (-20x1,2) + (30x1,60))/60 = (25-24+48)/60 = 0,82 m
Toepassing: berekening van het zwaartepunt van een voorwerp
[bewerken]In de inleiding werd reeds het voorbeeld aangehaald van het gewicht als vervanging van de verzameling kleine krachtjes die in elk punt van een voorwerp aangrijpen. Men kan deze verzameling krachtjes vervangen door één enkele resultante, nl. het gewicht. Het punt waarop dat aangrijpt, heet het zwaartepunt van het voorwerp. Wanneer men het voorwerp beschouwt als opgebouwd uit een verzameling puntmassa's mi, dan is de kracht op elke puntmassa mig. Zij M de totale massa van het voorwerp, dan is de R=Mg . Bij invullen in de formules kan de factor g weggedeeld worden, zodat er overblijft:
Of volgens de cartesische coördinaten:
Opmerkingen
1. Als het systeem een symmetrievlak of een symmetrieas heeft, zal het zwaartepunt in dat symmetrievlak of op die symmetrieas moeten liggen.
Onderstelt men bv. dat het zx-vlak een symmetrievlak is, dan betekent dit dat er voor elk punt met massa mi en coördinaat yi er ook een punt met massa mj = mi en coördinaat yj = -yi moet zijn. Bij sommeren over alle massa's vallen die tegen elkaar weg en eindigt men met een yZ=0, m.a.w. in het xz-vlak.
Op analoge manier kan men aantonen dat bij aanwezigheid van een symmetrieas het zwaartepunt op die symmetrieas moet liggen. Zij bv. de z-as een symmetrieas. Dan moet er voor elk punt met massa mi en coördinaat xi en yi ook een punt zijn met massa mj = mi en coördinaat xj = -xi en yj = -yi. Bij sommeren over alle massa's zal men dus komen op een xZ=0 en yZ=0 d.i. op de z-as.
2. Het zwaartepunt van een systeem hoeft niet noodzakelijk een materieel punt van dat systeem te zijn. Bij een holle bol zal het zwaartepunt samenvallen met het centrum van de bol, maar daar is geen massa aanwezig.
3. Daar het hier over een som gaat, kan men die opsplitsen in deelsommen. In de praktijk betekent dit dat men een voorwerp mag opdelen in eenvoudige delen, waarvan men gemakkelijk het zwaartepunt kan berekenen. Daarna kan men die zwaartepunten combineren tot het zwaartepunt voor het hele systeem.
Voorbeeld
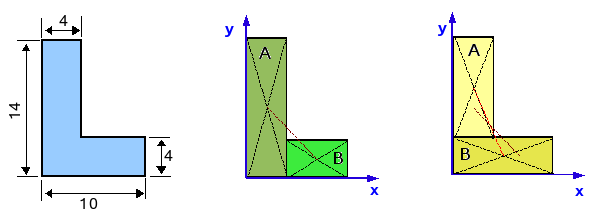
Men vraagt het zwaartepunt te berekenen van een L-vormige plaat met afmetingen zoals gegeven op de figuur.
Oplossing: men kan deze constructie opsplitsen in twee rechthoekige stukken, waarvan het zwaartepunt eenvoudig te bepalen is. Voor een rechthoek valt dat namelijk in het midden van de rechthoek. Grafisch kan men dat midden best bepalen door de diagonalen te trekken. Er zijn echter twee mogelijkheden om van deze L twee rechthoeken te maken; beide moeten uiteindelijk tot hetzelfde zwaartepunt leiden.
Eerste aanpak
Deel A is 4 bij 14 cm. Dus oppervlak = 56 cm2 en zwaartepunt ligt in (2,7)
Deel B is 6 bij 4 cm. Dus oppervlak = 24 cm2 en zwaartepunt ligt in (7,2)
Totale oppervlakte is 56 + 24 = 80 cm2. In de formules moet met de massa gerekend worden. Die kan men bekomen door het oppervlak te vermenigvuldigen met de massa per cm2 van de plaat. Deze factor wordt echter weggedeeld in de formules, zodat het resultaat alleen afhangt van de verhouding van de oppervlakten.
Zwaartepunt van het geheel:
- xz = (56x2 + 24x7)/80 = 280/80 = 3,50
- yz = (56x7 + 24x2)/80 = 440/80 = 5,50
Daar het zwaartepunt een lineaire combinatie is van de coördinaten van het centrum van A en B, moet het zwaartepunt van het geheel op de lijn liggen die beide zwaartepunten verbindt volgens een afstand die omgekeerd evenredig is met de massa van elk deel.
Tweede aanpak
Deel A is 4 bij 10 cm. Dus oppervlak = 40 cm2 en zwaartepunt ligt in (2,9)
Deel B is 10 bij 4 cm. Dus oppervlak = 40 cm2 en zwaartepunt ligt in (5,2)
Totale oppervlakte is natuurlijk weer 40 + 40 = 80 cm2
Zwaartepunt van het geheel:
- xz = 40 x (2 + 5)/80 = 280/80 = 3,50
- yz = 40 x (9 + 2)/80 = 440/80 = 5,50
Wanneer men beide verbindingslijnen van de centra van A en B samenbrengt op één figuur, dan moet het snijpunt het zwaartepunt van het geheel zijn. Daar beide lijnen elkaar onder een kleine hoek snijden, is de nauwkeurigheid van deze methode echter niet groot.
Opmerking
Dat opsplitsen in onderdelen kan ook gebruikt worden om een voorwerp te beschrijven als een eerste voorwerp waarvan men een tweede afgetrokken heeft, bv. een plaat met een gat in. Men heeft dan positieve en negatieve termen als in het voorbeeld van de krachten op een paal in de vorige paragraaf.

Als voorbeeld wordt een ronde plaat beschouwd met een ronde opening erin zoals afgebeeld op de figuur. Het zwaartepunt y1 van de volledige plaat (zonder gat) ligt in de oorsprong, dat van het uitgesneden stuk in y2 = -10 cm. Als men de massa van de plaat per cm2 voorstelt door m kg/cm2, de massa van de volledige plaat als M1 kg en de massa van het uitgesneden stuk als M2 kg dan geldt:
Omwille van symmetrie moet ook het zwaartepunt van de plaat met het gat erin op de y-as vallen. De waarde van de y-coördinaat wordt bepaald door:
Dit is maar een kleine verschuiving, maar men mag niet vergeten dat het uitgesneden stuk maar 1/9e is van de totale plaat.
Vlakke systemen
[bewerken]Bij een vlak systeem staan alle momenten als resultaten van een vectorieel product loodrecht op het vlak van de posities en de krachten. Die momenten hebben ook maar één component. Als men het vlak van posities en krachten als xy-vlak neemt, dan liggen de momenten volgens de z-as. De vergelijking (2) wordt dan zeer eenvoudig. Schrijft men de positievector met coördinaten (x,y) en de resultante met coördinaten (X,Y), dan wordt (2):
- μO = xY - yX
Dit is de vergelijking van een rechte, om redenen hoger uitgelegd. Men kan het snijpunt met de x-as vinden door y = 0 te stellen of het snijpunt met de y-as door x = 0 te stellen. Men kan het resultaat ook interpreteren als de positie waar men de resultante R moet plaatsen, zodat ze daar een moment gelijk aan μO heeft t.o.v. de oorsprong. Dan is de resultante alleen in die positie equivalent met het systeem (R, μO) in de oorsprong.
Samenlopende krachten
[bewerken]Als de dragers van verscheidene krachten door één punt passeren, dan kan men dat punt kiezen als herleidingspunt. Daar geen enkele kracht een moment heeft t.o.v. dat punt, kan men in dat punt een equivalent systeem bouwen dat gewoon bestaat uit de som van alle krachten.
De schroefas
[bewerken]
Wanneer men de formule (1) bekijkt, dan ziet men dat de correctieterm
loodrecht moet staan op R. Wanneer men μO kan splitsen in een component μ1 evenwijdig aan R en een component μ2 loodrecht op R, dan kan alleen de laatste weggewerkt worden door naar een ander herleidingspunt over te gaan. Aan de component evenwijdig aan R zal nooit iets veranderen. Men kan R en de component μ1 evenwijdig aan R beschouwen als invarianten van het systeem. Tezelfdertijd is dat ook de minimale waarde van μP. De drager van dat systeem noemt men daarom ook de schroefas. Wanneer men een schroef indraait met een schroevendraaier, dan oefent de hand op die schroevendraaier een kracht en een moment uit die door evenwijdige vectoren voorgesteld worden. In het Engels denkt men eerder aan het indraaien van een bout want daar heet dit een systeem van krachten herleiden tot een "wrench".
Om de positie te vinden waarbij het systeem tot deze invarianten herleidt wordt zal men de evenwijdigheid van μP en R uitdrukken als
Wanneer men dit invult in (1) krijgt men als vergelijking van de schroefas:
Wanneer men de onbekende positie schrijft met cartesische coördinaten (x,y,z) en de resultante met coördinaten (X,Y,Z) dan levert dit het stelsel:
Dit is een systeem van 3 vergelijkingen in 4 onbekenden. De oplossing is dus een rechte. De normale oplossingsvolgorde is:

- k bepalen
- het moment bepalen als k.R
- de gevonden k invullen in het systeem en hieruit 2 vergelijkingen in x, y en z halen. Dit zijn vergelijkingen van vlakken. De snijlijn van die vlakken vormt de schroefas.
Voor k > 0 hebben resultanten en moment zelfde zin, voor k < 0 hebben ze tegengestelde zin.
Voorbeeld
Twee krachten zijn gelegen als in de figuur. Beide hebben de grootte F.
Intuïtief kan men hier de schroefas vinden. Beide krachten hebben gelijke en tegengestelde
componenten volgens de x-as. Die zullen dus een koppel vormen. De componenten volgens de z-as zijn evenwijdig en met zelfde zin. Die zullen de resultante leveren.
Om de vergelijking gemakkelijk te kunnen opstellen, maakt men liefst een tabel met alle gegevens.
| x | y | z | Fx | Fy | Fz | Mx | My | Mz | |
| F1 | 0 | 0 | c | 0 | 0 | ||||
| F2 | a | 0 | 0 | 0 | 0 | 0 |
Optellen van de componenten van de krachten levert als resultante:
Wanneer men, om de uitdrukkingen wat lichter te maken, stelt:
dan worden de vergelijkingen voor de schroefas:
Uit de tweede vergelijking volgt dadelijk:
Hiermede krijgt men voor het moment van de schroefas:
Dit invullen in de eerste en laatste vergelijking levert:
Het eerste resultaat is een vlak loodrecht op de z-as, het tweede een vlak loodrecht op de x-as beide door het midden van de balk. De snijlijn is een lijn evenwijdig aan de y-as door het midden van de balk. Dat is de positie van de schroefas.
Nawoord
[bewerken]Op he einde van de inleiding werd reeds gesteld dat de theorie veel breder toepasselijk is dan alleen op krachten, nl. op alle vectorsystemen waarbij men gebruik maakt van de som van die vectoren en van de som van hun momenten t.o.v. een punt of as. In het Frans noemt men zo'n systeem "un torseur" (niet te verwarren met "tenseur" = tensor), in het Duits spreekt men van Dyname, in het Engels van "wrench" (zie Screw theory). De krachten en hun momenten t.o.v. een punt vormen zo'n systeem, maar ook impuls en impulsmoment, rotaties en lineaire snelheden als gevolg hiervan. Deze laatste worden immers ook via een vectorieel product van rotatievector en positievector berekend. (zie Kinematica, 4.3 Samenstellen van rotaties)
De verplaatsingsformule kan daarbij dikwijls nuttig gebruikt worden. Het impulsmoment van een vrij bewegend voorwerp t.o.v. een ander punt dan het massacentrum, kan ermee berekend worden. Zie Voorwerpendynamica, Het massacentrum, impulsmoment van een vrij bewegend voorwerp. Zie ook bv. het voorbeeld van de draaiende balk, waarbij de momenten opgeschreven worden t.o.v. een hoekpunt in Voorwerpendynamica, algemene rotatie, hoofdtraagheidsassen, derde figuur. De verplaatsingsformule laat ook toe om de rotatievergelijking op te schrijven t.o.v. een ander punt dan het massacentrum. Zie rotatie rond as met vaste richting, basiswet, de opmerking aan het einde van de paragraaf.
Het is eigenaardig dat deze theorie in haar algemeenheid reeds meer dan 50 jaar in zowat alle Franse boeken staat (zie bv. [gruber] in de bibliografie), ook vrij frequent voorkomt in de Duitse, niet echt systematisch uitgewerkt wordt in de gewone Engelstalige handboeken.

































![{\displaystyle y_{z}={\frac {M_{1}.y_{1}-M_{2}.y_{2}}{M_{1}-M_{2}}}={\frac {m.\pi [30^{2}.0-10^{2}(-10)]}{m.\pi (30^{2}-10^{2})}}={\frac {1000}{800}}=1.25\ \mathrm {cm} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9e94b822fe6240cc755cae6477d999f14aa0a8c)




















