Klassieke Mechanica/Wrijving
Wrijving
[bewerken]Inleiding
[bewerken]Men kan hier op aarde bijna geen enkele beweging uitvoeren zonder dat er wrijving bij betrokken is. De formulering van de eerste wet van Newton, die zegt dat een voorwerp met een constante snelheid zal blijven bewegen als er geen netto kracht op werkt, is daarom helemaal niet evident. Ze onderstelt immers dat men de wrijving erkent als een kracht die de beweging tegenwerkt. De wet is dan ook eerst geformuleerd als conclusie uit de studie van de hemellichamen, die geen last hebben van wrijving. Hier op aarde is de ervaring eerder dat elke beweging waarop geen kracht werkt om die beweging in stand te houden, de neiging heeft om uit te doven.
Men kan verschillende soorten wrijving onderscheiden:
- de droge wrijving of slepende wrijving, dit is de wrijving tussen twee voorwerpen die tegen elkaar drukken en zich ten opzicht van elkaar verplaatsen.
- de rollende wrijving. Om bijvoorbeeld een spoorwegwagon in beweging te brengen op een horizontaal spoor, blijkt een kracht nodig te zijn die evenredig is met het gewicht van de wagon. Het mechanisme dat hiervoor verantwoordelijk is noemt men rollende wrijving. Het heeft echter niets te maken met de droge wrijving.
- de viskeuze wrijving bij beweging van een voorwerp in een fluïdum (vloeistof of gas). De studie hiervan behoort meer tot de hydrodynamica.
Hier zal op de eerste plaats de droge wrijving besproken worden. Men moet een onderscheid maken tussen de kracht waarmee de twee contactoppervlakken tegen elkaar gedrukt worden en de eigenlijke wrijvingskracht. De eerste kracht staat loodrecht op het contactoppervlak en noemt men de normale kracht. Symbool: meestal N. De tweede ligt in het contactoppervlak. Symbool: W.

Men kan in verband met de wrijving een aantal wetten formuleren. Deze gelden echter maar bij vrij harde voorwerpen (het ene voorwerp mag het oppervlak van het andere niet indeuken) en bij lage snelheden. Wanneer men op een blok dat in rust ligt op een horizontaal vlak een geleidelijk toenemende horizontale kracht laat werken, dan stelt men vast dat het blok gedurende een eerste fase in rust blijft om ten slotte, bij een kritische waarde van de horizontale kracht, in beweging te komen. Dit onderstelt dat de wrijvingskracht in het begin steeds gelijk blijft met de horizontale kracht, met andere woorden toeneemt met die horizontale kracht. Bij het overschrijden van de kritische waarde echter groeit de wrijvingskracht niet meer mee, is er een netto kracht en komt het voorwerp in beweging.
Slepende wrijving
[bewerken]De verhouding tussen de normale kracht en de wrijvingskracht noemt men de wrijvingscoëfficiënt, symbool: f. Deze verhouding past zich dus aan tot er een maximale waarde bereikt is. Er zijn twee manieren om het onderscheid te maken tussen de veranderlijke wrijvingscoëfficiënt in de eerste fase en de constante wrijvingscoëfficiënt tijdens de beweging:
- Men noemt wrijvingscoëfficiënt de verhouding tussen normale kracht en wrijvingskracht zoals die gedurende de eerste fase optreedt. De constante waarde die optreedt tijdens een beweging noemt men dan de maximale wrijvingscoëfficiënt, symbool: fmax..
- Men noemt wrijvingscoëfficiënt de maximale waarde die de verhouding tussen normale kracht en wrijvingskracht kan aannemen. De verhouding tijdens de eerste fase heet dan de effectieve wrijvingscoëfficiënt, symbool: feff. Hier zal deze laatste definitie worden gevolgd.
Als verhouding tussen twee krachten is de wrijvingscoëfficiënt f een dimensieloze grootheid.
In sommige omstandigheden is er een kleinere kracht nodig om het blok in beweging te houden dan om het in beweging te krijgen. Men maakt dan een onderscheid tussen de statische wrijvingscoëfficiënt en de dynamische wrijvingscoëfficiënt.
De wrijvingskracht is altijd tegengesteld aan de beweging of aan de zin waarin men het voorwerp probeert te doen bewegen. Het is dus een beetje een kameleonkracht, die zich aanpast aan de omstandigheden.
Men kan normale kracht en wrijving samenstellen tot één kracht die men de totale reactie noemt. Deze totale reactie R maakt met de normale kracht N een hoek φ, die de wrijvingshoek heet. Het is duidelijk dat
Vele problemen van wrijving kunnen op een elegante manier grafisch worden opgelost als men met deze totale reactie werkt.
I.v.m. de wrijving kunnen volgende wetten geformuleerd worden.
- De wrijvingskracht is evenredig met de normale kracht
- De wrijvingskracht is niet afhankelijk van de grootte van het contactoppervlak.
- De wrijvingskracht is afhankelijk van de aard van de contactoppervlakken.
- Bij kleine snelheden is de wrijvingskracht onafhankelijk van de snelheid.
De tweede wet is natuurlijk wel eigenaardig, maar is experimenteel vastgesteld. De verklaring zoekt men in het feit dat, op microscopische schaal, er in feite zeer weinig contacten zijn tussen de oppervlakken. Op microscopische schaal zien de meeste oppervlakken er vrij ruw uit, eerder als grof schuurpapier. Als men bij zelfde normale kracht het (macroscopische) contactoppervlak verkleint, dan komt er een grotere kracht per vierkante centimeter, een grotere druk op de oppervlakken. Hierbij zal het microscopische contactoppervlak vergroten en zal daardoor de wrijvingskracht toenemen.
De toestand van de contactoppervlakken heeft natuurlijk een grote invloed op de wrijvingscoëfficiënt. Wat men in de litteratuur vindt moet men dan ook als een eerste benadering beschouwen. Uitgebreide tabellen met wrijvingscoëfficiënten kan men bv. vinden op http://www.roymech.co.uk/Useful_Tables/Tribology/co_of_frict.htm#coef . Een paar waarden:
| materialen | f |
|---|---|
| Staal op staal | 0,4 - 0,8 |
| Koper op koper | 0,7 - 1,2 |
| Eik op eik | 0,3 - 0,6 |
| Hout op metaal | 0,2 - 0,5 |
| Hout op hout | 0,2 - 0,6 |
Om de wrijving te verminderen worden smeermiddelen gebruikt. Dan vermindert niet alleen de wrijving, maar het gedrag van de resterende wrijving is ook anders dan bij de droge wrijving. Er zal meer invloed zijn van de snelheid. Meestal geldt: hoe hoger de snelheid, hoe lager de wrijving. Wanneer de viscositeit van de smeermiddelen sterk verandert met de temperatuur, kan ook de temperatuur een grote invloed hebben.
Bij problemen met wrijvingskrachten moet men zich altijd de vraag stellen of de wrijvingskracht maximaal is of niet. De wrijvingskracht zal maximaal zijn als de voorwerpen langs elkaar bewegen of op het punt staan te gaan bewegen. Als de wrijvingskracht niet maximaal is, dan heeft men een feff die zeker een onbekende is van het probleem.
Voorbeeld 1: blok op hellend vlak
[bewerken]
Als eerste voorbeeld wordt een blok op een hellend vlak beschouwd. Het blok heeft een gewicht G, de hoek van de helling is α en de wrijvingscoëfficiënt is f. Gevraagd wordt welke kracht F, parallel met de helling, er nodig is om te beletten dat het blok naar beneden schuift.
Oplossing
Het gewicht heeft een component langs de helling die het blok naar beneden duwt en een component loodrecht op de helling die zorgt voor het ontstaan van een normale kracht N. Voor evenwicht moet gelden:

Projecteert men dit op een schuin assenkruis dan krijgt men:
- (1)
- (2)
En ten slotte de wrijvingswet: W= f.N (3)
Dit levert 3 vergelijking in 3 onbekenden F, N en W. Dit is dus oplosbaar.
Men substitueert (3) in (1) en elimineert N. Dit levert:
Hieruit blijkt dat F = 0 is voor sin α = f.cos α of tan α = f = tan φ d.i. als de maximale wrijvingshoek gelijk is aan de hoek van de helling. Is de hoek van de helling kleiner, dan komt er een negatieve oplossing uit de bus. Dit betekent dat men nog aan het blok zou moeten trekken om het naar beneden te laten bewegen. Doet men dat niet, dan is er evenwicht mogelijk voor een feff die kleiner is dan de maximale waarde, onafhankelijk van het gewicht van het blok! Het gebeurt bij problemen van wrijving wel meer dat men een negatief resultaat bekomt voor een kracht, terwijl dit niet zinvol is. Meestal is het te wijten aan het ten onrechte onderstellen van maximale wrijving en moet het resultaat geïnterpreteerd worden als: " er is altijd evenwicht mogelijk zonder dat er maximale wrijving nodig is".
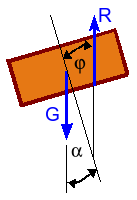
Denkt men in termen van de totale reactie R dan zal er evenwicht zijn als R de tegengestelde vector is van G. Dit zal altijd mogelijk zijn als α <= φ . Het gewicht van het blok speelt geen rol omdat zowel N als W groeien met het gewicht van het blok. Om te voldoen aan de momentenvergelijking moet R ook nog in het verlengde liggen van G, maar dit levert hier geen probleem.
Een analoge situatie ontstaat als men met een spie een deur wil vastzetten. Dan is het de druk van de deur die de rol van het gewicht overneemt. Deze druk zal loodrecht staan op de schuine zijde van de spie en zorgt voor een kracht met een component die de spie tegen de grond drukt en een component die de spie wil wegduwen. Zolang de hoek van de spie kleiner is dan de maximale wrijvingshoek die overeenkomt met de wrijvingscoëfficiënt tussen spie en vloer, zal de deur geklemd blijven. Bij een gladde vloer moet men dus een spie met een kleine hoek gebruiken of een rubberen spie die een grotere wrijvingscoëfficiënt heeft.
Voorbeeld 2: variant
[bewerken]Als tweede voorbeeld kan men een variant op de vorige situatie beschouwen. Laat de hoek van de helling groter zijn dan de maximale wrijvingshoek (beide gegeven). Dan zal het blok niet in rust blijven liggen. Men kan nu echter vragen naar de kleinste kracht die nodig is om te beletten dat het blok naar beneden schuift en de kleinste kracht die nodig is om het blok omhoog te doen bewegen en de hoek β waaronder die kracht moet trekken.
Oplossing
In beide situaties zal de wrijvingskracht maximaal zijn en mag men de wrijvingscoëfficiënt f als bekend beschouwen. Men moet beide situaties echter afzonderlijk behandelen.
- Minimale kracht om te beletten dat het blok naar beneden beweegt: in dat geval is de wrijving naar omhoog gericht.
- Minimale kracht om het blok omhoog te trekken: in dat geval is de wrijvingskracht naar beneden gericht.
Zij β de hoek van F met de helling. Men kan dit probleem op een zuiver algebraïsche manier oplossen. Men kan dit probleem ook op een zeer elegante manier grafisch oplossen, waardoor de algebraïsche oplossing plots veel zinvoller wordt.
1. Algebraïsche oplossing
a. Blok mag niet naar beneden bewegen.
Men krijgt de vergelijkingen als hierboven, maar nu met 2 componenten voor F:
De wrijvingswet: W= f.N
Dit stelsel bevat 4 onbekenden voor 3 vergelijkingen. Men zal F moeten berekenen als functie van β en dan het minimum van deze functie moeten bepalen. Men vindt op vrij eenvoudige manier:
Met de substitutie f = tg φ is dit om te vormen tot:
- of
β blijkt alleen in de noemer voor te komen. F zal dus minimaal zijn als de noemer maximaal is. De cosinusfunctie kan maximaal 1 worden voor een hoek van 0°. F wordt dus minimaal voor β + φ = 0 of β = -φ. Daar de helling een hoek α maakt met de horizontale, is dit ook een hoek α - φ t.o.v. de horizontale. Daarbij is
b. Minimale kracht om het blok omhoog te trekken
Het teken van de wrijving verandert, de rest van de vergelijkingen blijft hetzelfde. Dit leidt tot volgend resultaat:
Met dezelfde redenering als hierboven komt men tot de conclusie dat β = φ of dat de hoek van F t.o.v. de horizontale = α + φ. Daarbij is F dan:
2. Grafische oplossing

De oplossingen die hierboven gevonden werden voor F zijn van een intrigerende eenvoud. De grafische aanpak toont waarom.
Voor evenwicht moet de som van de krachten = 0 zijn. Dit betekent dat de betrokken vectoren een gesloten veelhoek moeten vormen. De eerste vector stelt het gewicht voor. Dit is een vector waarvan richting en grootte vastliggen. De tweede vector is de totale reactie. Als men wil beletten dat het blok naar beneden schuift, dan ligt die reactie onder een hoek φ rechts van de normale op de helling. De grootte ervan ligt niet vast. De kracht F moet de driehoek sluiten. Als men een minimale F wil, dan komt dat neer op een minimale afstand tussen het beginpunt van G en de drager van de totale reactie. Die minimale afstand wordt bereikt door een loodlijn uit het beginpunt van G op die drager (dikkere lijn). Men krijgt dan een rechthoekige driehoek met G als schuine zijde en een hoek (α - φ) tegenover F.

Dit levert dus de hoger gevonden eenvoudige oplossing voor de grootte van F. De richting ervan blijkt ook onder een hoek (α - φ) te liggen ten opzichte van de horizontale.
Voor de minimale kracht om het blok omhoog te trekken, krijgt men een analoog verhaal. Alleen ligt de drager van de totale reactie nu links van de normaal op de helling, onder een hoek (α + φ) t.o.v. de verticale. De minimale waarde wordt weer bereikt bij een loodrechte afstand van het beginpunt van G naar die drager van R. Men krijgt zo weer een rechthoekige driehoek maar nu met een hoek (α + φ) tegenover F.
Voorbeeld 3: ladder tegen muur
[bewerken]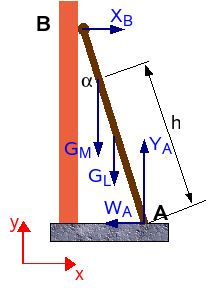
Als volgend voorbeeld wordt een ladder beschouwd die tegen een muur geplaatst is. De lengte van de ladder is l, zijn gewicht GL en hij staat onder een hoek α met de verticale. Voor de eenvoud van de zaak onderstelt men dat de ladder bovenaan met wieltjes langs de muur rolt. Er is dan alleen een horizontale reactie van de muur op de ladder. Onderaan is er wrijving tussen ladder en grond met wrijvingscoëfficiënt f. Op de ladder kruipt een man met gewicht GM. Hij bevindt zich op een hoogte h boven de grond, langs de ladder gemeten. Wat is het verband tussen de maximale hoek α en f?
Oplossing
Men kan dit probleem weer zuiver algebraïsch of grafisch oplossen. Voor een algebraïsche oplossing moet men de 3 vergelijkingen voor het evenwicht van de ladder opschrijven en de wrijvingswet.
- moment t.o.v. A
Wrijvingswet: WA = f.YA
Men vindt:
Drukt men de hoogte h uit als een fractie p van l, namelijk als h = p.l met 0<=p<=1, dan wordt dit:
Het is duidelijk dat de noemer van de breuk altijd kleiner zal zijn dan de teller. De breuk heeft dus altijd een waarde groter dan 1. De hoek α mag dus iets groter worden dan de maximale wrijvingshoek φ. Als men binnen deze maximale wrijvingshoek φ blijft, zit men zeker veilig.

Bemerk dat de situatie kritischer wordt naarmate de man hoger klimt op de ladder. Men zou normaal denken dat het steunpunt onderaan altijd het volle gewicht van man en ladder moet dragen en dat de positie van de man dus weinig uitmaakt. Het probleem is echter dat de vereiste wrijvingskracht stijgt met de hoogte van de man. Als de man op de top van de ladder staat, is er een grotere horizontale reactie van de muur vereist voor het momentenevenwicht. Deze grotere reactie vraagt op haar beurt voor een grotere tegengestelde wrijvingskracht in het contactpunt met de grond en zo wordt de situatie kritischer met de hoogte van de man.
Voor de grafische oplossing zal men bedenken dat het evenwicht van de momenten van drie niet evenwijdige krachten vereist dat ze alle drie door één punt gaan. Om tot drie krachten te komen moet men eerst het gewicht van de man en ladder samenstellen tot een totaal gewicht. De drager hiervan zal ergens tussen A en B passeren afhankelijk van de positie van de man. Als de man op de top van de ladder staat, passeert de drager dicht bij B. Het snijpunt van de horizontale reactie in B met deze drager zal dan dicht bij B op de horizontale door B liggen. Verder werkt men weer met de totale reactie in A. Die moet dus ook door dat snijpunt passeren. Daaruit blijkt dus dat de ladder iets schuiner mag staan dan de maximale wrijvingshoek φ en dus te meer naarmate het gewicht van de ladder groter is in verhouding tot het gewicht van de man. Hieruit blijkt ook dat lichte aluminium ladders met de nodige zorgvuldigheid moeten gebruikt worden!
Voorbeeld 4: lijmklem
[bewerken]
Door schrijnwerkers wordt dikwijls beroep gedaan op lijmklemmen (zie foto) om stukken vast te klemmen. In het Frans heet dit instrument "serre-joint". In sommige Vlaamse streken werd dat verbasterd tot "sergeant". Als men de truc niet kent om de beweeglijke arm te verschuiven, dan kan dit een zeer nukkig instrument zijn. Het blijkt dat er een minimale afstand nodig is tussen de staaf waarover deze arm glijdt en de schroef waarmede men de stukken vastzet.
Wanneer er een kracht uitgeoefend wordt op de kop van de schroef, dan zal de arm lichtjes kantelen zodat hij maar in twee diagonaal tegengestelde punten nog contact maakt met de staaf. Hier is dat in de punten A en C. Men kan de minimale afstand d weer zuiver algebraïsch of grafisch bepalen. De momentenvergelijking speelt weer een belangrijke rol, zoals bij de ladder tegen een muur hierboven. Als men deze opschrijft t.o.v. het punt C, dan kan men zeggen dat het moment van de kracht F een tegengesteld moment vraagt van YA. Wanneer d klein is zal ook YA kleiner uitvallen. Dat leidt dan weer tot een kleinere maximale wrijvingskracht, die uiteindelijk de arm op zijn plaats moet houden. Het blijkt weer dat de grootte van F geen rol speelt, daar de reactiekrachten en de wrijvingskrachten evenredig met F toenemen. Alleen de afstand d speelt een cruciale rol in functie van de wrijvingscoëfficiënt en van de afmetingen van de opening in de arm.

Algebraïsche oplossing
De vergelijkingen worden:
- (1)
- (2)
- (3) momenten t.o.v. C
Uit (2) volgt dat YA = YC, waaruit dan weer volgt dat WA = WC. De eerste vergelijking wordt dus F = 2fYA . Alles invullen in de momentenvergelijking levert:
- 2dfYA = YA(a - fb) of
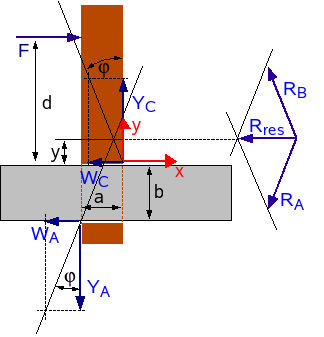
Grafische oplossing
Voor de grafische oplossing werkt men weer met de totale reactie. Voor evenwicht zullen de twee totale reacties zich moeten samenstellen tot één resultante die tegengesteld is aan F en op dezelfde drager ligt. Dit samenstellen zal gebeuren in het snijpunt van de twee dragers (zie in het hoofdstuk over equivalente vectorsystemen de tekst over samenlopende krachten). Bij maximale hoek φ voor beide dragers, zal dit snijpunt het dichtst bij de staaf liggen.
Om de dragers te kunnen beschrijven, wordt een klassiek xy-assenkruis met oorsprong in C ingevoerd. De drager van de totale reactie door A is dan een rechte die door A(-a,-b) passeert en een richtingscoëfficiënt 1/f heeft. De vergelijking hiervan is:
De drager door C heeft een richtingscoëfficiënt -1/f. De vergelijking van deze rechte wordt
De minimale afstand d is de y-waarde van het snijpunt van beide lijnen. Lost men x op uit de laatste vergelijking en substitueert men dat resultaat in de eerste, dan vindt men als y-waarde:
- ... ut supra.

Als de hoek φ kleiner wordt, wordt de waarde van y groter. Bij de getekende waarde van d zal de maximale wrijving niet nodig zijn om y=d te maken.
Om de arm van een lijmklem zonder problemen te kunnen verschuiven, neemt men deze dus best vast dicht bij de staaf (zie foto). Of men moet aan de arm een rotatie geven die tegengesteld is aan de rotatie die hij normaal zou krijgen door ertegen te duwen. Als men de arm in de foto naar rechts wil bewegen, moet men er een moment op uitoefenen dat hem linksom probeert te draaien. Dat leidt dan tot contacten in B en D. Dat moment neutraliseert dan het moment van de schuifkracht, waardoor er geen wrijvingskrachten in A en C kunnen ontstaan.
Kantelen
[bewerken]
Wanneer men tegen een blok duwt dat met wrijving op de grond ligt, dan kan men de normale reactie en de wrijving samenstellen tot één totale reactie Rtot en het gewicht van het blok en de kracht waarmede geduwd wordt tot één resultante Rres, die moet passeren door het snijpunt van gewicht en duwkracht. Dit is voorgesteld in de rechtse figuur. Voor het evenwicht van de krachten moeten beide vectoren gelijk maar tegengesteld zijn, voor het momentenevenwicht moeten beide op dezelfde drager liggen. Naarmate men hoger gaat duwen zal deze drager in het voorbeeld meer naar links verschuiven, tot hij door het hoekpunt van het blok passeert. Duwt men nog hoger dan valt Rres links van Rtot. Er ontstaat een netto moment en het blok zal kantelen rond het hoekpunt van het blok. De grens voor kantelen treedt dus op als de normale reactie (of de totale reactie) aan de grens van het voorwerp komt. Als men een hoge kast wil verschuiven, dan moet men dus laag duwen tegen die kast.
De resultanten werden niet getekend in de linkse figuur om de figuur niet te overladen.
Indien het blok een breedte b heeft, dan zou men, steunend op de figuur, de kritische hoogte yF voor de kracht F kunnen berekenen als
- yF = b/(2.tg φ) = b.cotg φ/2
Voor de algebraïsche aanpak moet men de volgende vergelijkingen opschrijven:
- W - F = 0 of W = F
- N - G = 0 of N = G
Momenten t.o.v. het linkse hoekpunt:
- yF.F - (b/2).G = 0
En ten slotte:
- W = f.N
Uit de eerste twee vergelijkingen en de wrijvingswet volgt: G = F/f . Vult men dat in in de momentenvergelijking, dan bekomt men:
- yF = b/(2.f) of ... ut supra.
Rollen met slippen
[bewerken]De wrijving die optreedt tussen de grond en een rollend voorwerp of tussen twee tegen elkaar rollende voorwerpen, vormt een beetje een speciaal geval. Het is immers niet altijd duidelijk wat de zin van de wrijving zal zijn noch of er zuiver rollen dan wel rollen met slippen zal optreden.

Het eenvoudigste geval is dat waar de wrijving noodzakelijk is voor de rotatie van het voorwerp. Dat is bv. het geval wanneer men aan de as van een rol trekt. Dan moet de wrijving met de grond zorgen voor de rotatie rond die as. Als er geen wrijving is, dan zal de rol glijden i.p.v. rollen. In de figuur hiernaast is de wrijving nodig voor de rotatie, maar werkt ze de translatie tegen. Men krijgt als vergelijkingen:
- voor de translatie:
- voor de rotatie t.o.v. het massacentrum:
Nu is de vraag of er zuiver rollen is of rollen met slippen. Men kan eerst onderstellen dat er zuiver rollen is en berekenen welke wrijvingscoëfficiënt hiervoor nodig is. Blijkt die groter dan wat fysisch mogelijk is, dan moet men besluiten dat er rollen met slippen zal optreden en de berekeningen herbeginnen met een paar kleine wijzigingen.
Voor zuiver rollen geldt de bindingsvergelijking:
De wrijvingscoëfficiënt moet dan berekend worden uit
Dit is een systeem van 4 vergelijkingen in de onbekenden W, feff, ac en α.
Als blijkt dat er rollen met slippen op treedt, dan moet men de bindingsvergelijking laten vallen. Maar dan verdwijnt ook f als onbekende uit de vergelijkingen want die wordt dan gewoon de bekende maximale wrijvingscoëfficiënt.
Numeriek voorbeeld
Zij in bovenstaand voorbeeld m = 2 kg, r = 0,2 m, I = m.r2/2 = 0,04 kgm2 = 1/25 kgm2, F = 10 N
Voor de eenvoud van de berekeningen wordt g = 10 m/s2 genomen (fout < 2%!)
Dan is G = 20 N
Uit de vergelijkingen blijkt dat voor rollen feff = F/3G = 10/3.20 = 0,166...
Eerste geval : f = 0,2
In dit geval heeft men dus rollen. Uit de vergelijkingen volgt:
aC = 2F/3m = 2.10/3.2 = 10/3 m/s2 = 3 1/3 m/s2
α = aC/r = 10/3.0,2 = 50/3 rad/s2 = 16 2/3 rad/s2
Als men de zaak nu vanuit energetisch standpunt bekijkt, moet de arbeid geleverd door F omgezet zijn in kinetische energie. Na 1 s moet dan gelden:
s = aC.t2/2 = 10.12/3.2 = 10/6 m = 1 2/3 m
vC = aC.t = 10/3 m/s = 3 1/3 m/s
ω = α.t = 50/3 rad/s = 16 2/3 rad/s
A = F.s = 10.10/6 = 50/3 J = 16 2/3 J
Ek = mvC2/2 + Iω2/2 = 2(10/3)2/2 + 0,04(50/3)2/2 = 50/3 J = 16 2/3 J
De arbeid die wordt geleverd door F is dus inderdaad terug te vinden als kinetische energie.
Tweede geval : f = 0,1
Hiermede zit men in het gebied van rollen met slippen. Uit de vergelijkingen volgt:
F - f.G = m.aC waaruit aC = (10 - 0,1.20)/2 = 4 m/s2
α = 2.f.G/(mr) = 2.0,1.20/(2.0,2) = 10 rad/s2
Vanuit energetisch standpunt bekeken, na 1 s, met zelfde formules als hierboven:
s = 4.1/2 = 2 m A = 10.2 = 20 J
vC = 4 m/s ; ω = 10 rad/s
Ek = 2.42/2 + (1/2)(1/25).102 = 18 J
Wat ontbreekt is natuurlijk de energie die verloren gegaan is door wrijving bij het slippen. Om die uit te rekenen moet men eerst de absolute versnelling van het contactpunt met de grond kennen:
- aabs = aC - r.α = 4 - 0,2.10 = 2 m/s2
Met deze versnelling is er na 1s een afstand afgeleged van 2.1/2 = 1 m. De energie verloren door wrijving is dan W.s = 0,1.20.1 = 2 J . En hiermede sluit de balans als een bus.

Er zijn echter ook situaties waar er reeds een andere kracht is die zowel voor translatie als rotatie kan zorgen. Hiernaast het geval van een rol waaromheen een touw gewikkeld is. Als men aan het touw trekt, dan oefent men een kracht uit die de juiste zin heeft voor zowel de translatie- als rotatieversnelling. De zin van de wrijving is dus moeilijk op het zicht te voorspellen. Als het systeem uit rust vertrekt, kan men in deze situatie kijken wat er zou gebeuren met het contactpunt onderaan de rol als er geen wrijving is. Men kan volstaan met de versnelling van dat punt uit te rekenen, want als er een versnelling in een bepaalde zin is, dan zal er het volgende ogenblik een snelheid en een verplaatsing in die zin zijn. De wrijving zal zich tegen de verplaatsing van dat punt verzetten en dus de tegengestelde zin ervan hebben. Bemerk dat ook in vorig voorbeeld de juiste zin zo gevonden kan worden.
- Voor de translatie:
- Voor de rotatie t.o.v. het massacentrum:
- Versnelling van P:
Als het wiel een volle schijf is met I = m.r2/2, dan volgt uit de 2e vergelijking dat rα = 2F/m . Uit de 1e vergelijking volgt dat aC = F/m . Beide uitdrukkingen invoeren in de 3e vegelijking levert:
Het minteken betekent dat aP naar links gericht is. Men heeft immers de projecties die horizontaal naar rechts gericht zijn als positief genoteerd. De wrijving zal dus naar rechts wijzen, d.i. helpen bij de translatie maar tegenwerken voor de rotatie.
Men kan nu de vergelijkingen opstellen voor rollen met wrijving. Hierbij moet men weer beide mogelijkheden onderzoeken zoals hierboven. Dus:
- Voor de translatie:
- Voor de rotatie t.o.v. het massacentrum:
- Bij zuiver rollen:
- Wrijvingskracht:

Een meer intrigerende situatie is hiernaast geschetst. De eerste vraag die zich stelt is of er zuiver rollen naar rechts mogelijk is. Daarbij zou het touw immers opwinden i.p.v. afwinden. Deze vraag kan snel beantwoord worden als men de zaak weer vanuit energetisch standpunt bekijkt. De kracht F moet arbeid leveren als de zaak in beweging wil komen. Het touw moet zich dus naar rechts verplaatsen. Men weet dat het onderste punt van de rol het ogenblikkelijk rotatiecentrum is. Dan is het duidelijk dat bij rollen naar rechts het contactpunt van het touw met de rol zich ook naar rechts zal verplaatsen. De snelheid van het middelpunt van de rol naar rechts is groter dan de relatieve snelheid van dat contactpunt naar links. De wrijving is in elk geval naar links gericht. Men zal voor stijgende kracht F vier fases hebben: eerst een zuiver rollen naar rechts, dan een rollen met slippen, waarbij de rol nog altijd naar rechts draait, dan een zuiver schuiven van de rol als het moment van F t.o.v. de as van de rol gelijk is aan het moment van de wrijving, en ten slotte een slippen met de rol draaiend naar links (tegenwijzerzin).
Wrijving over gebogen oppervlak
[bewerken]
Een zeer speciaal geval van wrijving is de wrijving die optreedt wanneer een kabel rond een gebogen oppervlak gespannen wordt. Wanneer men een kabel, die gespannen staat onder een kracht F, een stukje rond een cirkelvormig voorwerp leidt, dan kan men voor de kracht van de kabel op het voorwerp opschrijven:
Dat hier voor een cirkelvormig voorwerp gekozen werd, doet niets af aan de algemeenheid van de afleiding want elke kromme kan men in een punt benaderen door een osculerende cirkel, d.i. een cirkel die zo nauw aansluit bij de kromme dat de eerste en tweede afgeleide dezelfde zijn als die van de kromme.
In de limiet voor Δφ gaande naar 0 krijgt men dN = F.dφ
Bij een wrijvingscoëfficiënt f geeft deze kracht aanleiding tot een wrijvingskracht dW = f.dN = f.F.dφ . Dit betekent dat er aan één zijde nu een kracht dF = dW meer mag aangrijpen zonder dat het evenwicht verbroken wordt. Of dF = f.F.dφ . Dit is een differentiaalvergelijking met als oplossing:
In woorden: als men aan het ene einde van een kabel trekt met een kracht F1 en die kabel wordt rond een voorwerp geleid zodat hij er een hoek φ is tussen begin een einde, dan mag er aan het andere einde getrokken worden met een kracht F2, die exponentieel stijgt met de hoek φ. Dit is een zeer sterke stijging. Voor berekeningen moet φ natuurlijk in radialen uitgedrukt worden, want dat is de enige coherente eenheid voor hoeken. Eén toer is dan 2π radialen. Een paar cijfers:
| f | toeren | exp(2.π.f.t) |
|---|---|---|
| 0,1 | 1 | 1,87 |
| 0,1 | 2 | 3,51 |
| 0,1 | 3 | 6,59 |
| 0,2 | 2 | 12,3 |
| 0,2 | 3 | 43,4 |

Hiervan wordt dagelijks gebruik gemaakt om lasten op te hijsen op schepen of op werven. Daar werkt men dikwijls met een horizontale of verticale kaapstander. Dit is een cilinder die continu draait. Om iets op te hijsen leidt men het losse einde van de kabel twee of driemaal rond deze cilinder en trekt aan. De man die aan het losse einde trekt hoeft maar een fractie van de kracht uit te oefenen die de kabel aan de andere zijde kan leveren. Laten stijgen of dalen van de last gebeurt niet door de snelheid van de cilinder te regelen, maar gewoon door meer of minder te trekken aan het losse einde van de kabel.
De foto toont hoe vroeger een kaapstander door een groep matrozen in beweging gebracht werd. Hij toont een deel van een maquette in het San Francisco Maritime Museum.
Een eenvoudig proefje laat ook zien hoe sterk het verschil in spanning aan beide zijden kan zijn. Men neemt een stekjesdoosje en een sleutelbos en verbindt beiden met een touwtje van 60 à 70 cm. Men leidt dit touwtje over een horizontale ronde staaf (de steel van een houten lepel bv.) zodat de sleutelbos dicht bij de staaf hangt en houdt het andere einde met het doosje horizontaal. Men lanceert het doosje naar beneden. Het blijkt dat na 3 of 4 toeren van het touw rond de staaf de sleutelbos in zijn val gestopt wordt. Het doosje van 8 à 10 g blijkt de sleutelbos van 100 g te kunnen tegenhouden!
Rollende wrijving
[bewerken]Wanneer een voorwerp verplaatst kan worden op wielen, dan weet men dat dit veel minder inspanning vraagt dan het voorwerp verslepen. Het gaat echter niet vanzelf. Ook om een fiets, kar of auto in beweging te houden op een vlakke weg, is een continue kracht nodig. Men zegt dat er een rollende wrijving moet overwonnen worden. Het mechanisme achter die rollende wrijving is echter complex. In feite zijn er veel verschillende mechanismen die spelen.

Een eerste oorzaak van rollende wrijving komt doordat een wiel in zijn contact met de grond altijd een beetje afgeplat wordt. Ook het materiaal waarop het wiel rust zal op die plaats lichtjes ingedeukt worden. Wanneer het wiel in beweging komt, moet het als het ware kantelen (zie vorige paragraaf) rond de voorzijde van deze afgeplatte strook. Dit betekent dat de normale resultante naar voor zal schuiven en daardoor vóór de as van het wiel zal wijzen. Hierdoor ontstaat een tegenwerkend moment, dat voortdurend moet overwonnen worden om de beweging in stand te houden. Het blijkt dat deze kracht, voor zelfde wielen op zelfde ondergrond, in een groot gebied evenredig is met het gewicht van het voorwerp. Vandaar dat men het ook als een soort wrijving beschrijft.
Wanneer het wiel rolt, wordt er natuurlijk telkens vooraan nieuw materiaal samengedrukt. Men zou kunnen denken dat het materiaal dat zich achteraan kan ontspannen hiervoor een compensatie levert, maar dat is niet zo. Geen enkel materiaal is volkomen elastisch, d.w.z. herstelt zich volledig en ogenblikkelijk na een indrukking. Elk materiaal heeft een zekere hysteresis, d.i. het bijhouden van een restje van de vorige toestand. Of meer wetenschappelijk is hysteresis het feit dat bij een vervormbaar materiaal de energie teruggegeven bij herstel van een vervorming, altijd kleiner is dan de energie die nodig was voor de vervorming. Dit heeft ook met inwendige wrijving te maken, die bij de indrukking een verlies van energie veroorzaakt i.p.v. een zuivere omzetting in potentiële energie. Vooral bij banden van fietsen en auto's speelt deze hysteresis een belangrijke rol in de rolweerstand. De energie die erdoor verloren gaat, wordt omgezet in warmte. Banden die te zacht opgepompt zijn, worden bij elke omwenteling van het wiel meer vervormd dan nodig en zullen dus meer opwarmen. Daarom moeten zeker bij een lange rit over een autosnelweg met een goed geladen wagen, zoals bij een vakantieuittocht dikwijls het geval is, de banden correct opgepompt zijn. Velen geven zelfs de raad om in die omstandigheden de banden een 100 g/cm2 harder op te pompen dan wat opgegeven wordt. Het energieverlies door de vervorming van de flanken van de band kan verminderd worden door een soepeler rubber te gebruiken voor de flanken (vooral bij fietsbanden).
Voor het karakteriseren van de rollende wrijving zijn twee systemen in gebruik. Het eerste systeem definieert een coëfficiënt voor rolweerstand Crw als de verhouding van de kracht nodig om de beweging in stand te houden over het gewicht zoals bij de slepende wrijving. Deze wrijvingscoëfficiënt is dan een dimensieloze grootheid, zoals die bij slepende wrijving. Enkele numerieke waarden (naar Rolling resistance in de engelstalige Wikipedia):
| Crw | materiaal |
|---|---|
| 0,0002 - 0,0010 | Stalen treinwiel op trein rail |
| 0,005 | Tramwiel op tramrail |
| 0,006 - 0,01 | banden met lage rolweerstand op een zeer vlakke baan |
| 0,01 - 0,015 | gewone banden op betonnen baan |
| 0,02 | auto op stenen platen |
| 0,030 | auto of bus op asfalt |
Het tweede systeem houdt rekening met de diameter van het wiel. Het gaat uit van de redenering dat, bij rollen over een vlakke ondergrond, een kleiner wiel een grotere indeuking zal veroorzaken dan een groot, door zijn grotere kromming in de contactzone. Dit zou een coëfficiënt moeten opleveren die in een breder gebied kan toegepast worden. Men vermenigvuldigt dan de vorige coëfficiënt met de straal van het wiel en bekomt zo een coëfficiënt die de dimensies heeft van een lengte. Om de kracht te berekenen moet men hier die coëfficiënt vermenigvuldigen met het gewicht van de last en delen door de straal van het wiel. Een stalen treinwiel op een treinrail zou dan een Crw = 0.5 mm hebben.
Het is pas op het einde van de 19e eeuw dat de kogel- en rollagers algemeen in gebruik gekomen zijn in de machinebouw. Een goed kogellager vereist immers zeer hard en goed gepolijst staal en zeer nauwe toleranties bij de constructie. Wie hierover meer wil weten kan een mooi geschiedkundig overzicht vinden op http://www.alexdenouden.nl/08/rolling1.htm en volgende pagina's.
Viskeuze wrijving
[bewerken]Dit onderwerp behoort tot de hydrodynamica of studie van de stroming van gassen en vloeistoffen. Voor de volledigheid wordt hier een kort woordje erover gezegd.
Wanneer een voorwerp beweegt in een vloeistof of gas, dan ondervindt het een tegenwerkende kracht die bij lage snelheid evenredig is met de snelheid en bij hogere snelheden evenredig met het kwadraat van de snelheid. Een steen die met een kleine beginsnelheid in het water valt, is een voorbeeld van het eerste geval, maar de beweging van een tennisbal valt onder de tweede wet. Wat in deze context als hoge of lage snelheid moet worden beschouwd, wordt bepaald door het reynoldsgetal (zie ook: Reynolds number in de Engelse Wikipedia). Dit getal is gedefinieerd als:
waarin:
- Re = reynoldsgetal
- ρ = dichtheid van het medium, vloeistof of gas
- l = karakteristieke lengte (voor bol of buis: diameter)
- v = snelheid van de stroming (of van het voorwerp in het medium)
- η : viscositeit van het medium
Een voorbeeld van een grafiek van de weerstandscoëfficiënt in functie van het reynoldsgetal vindt men in onderstaande figuur.

Hierbij stelt 2 het gebied voor met een continue stroming rondom de bol (het gebied van de wet van Stokes), 3 is het gebied met een stabiele stroming vooraan maar een stroming die stilaan turbulent wordt achter de bol, 4 is het gebied met onstabiele stroming vooraan een chaotische turbulente stroming achteraan en 5 is het gebied met turbulente stroming rondom de bol.
Waarden kleiner dan 10 beschouwt men als lage, tussen 103 en 105 als hoge reynoldsgetallen. Wanneer men in een laboratorium een proef op een schaalmodel uitvoert, moet men zorgen voor zelfde reynoldsgetallen. Voor een kleiner model betekent dit hogere snelheden of werken met een minder viskeus medium.
De bewegingsvergelijking van een bol die valt in een medium kan men schrijven als:
waarin:
- m = massa van het voorwerp
- m' = massa van het verplaatste medium, vloeistof of gas
- fm = tegenwerkende kracht van het medium, hier opwaartse kracht
1 - Lage reynoldsgetallen
Bij lage reynolds getallen is fm evenredig met de snelheid. Hiervoor geldt de bekende formule van Stokes ( ook bekend als formule van Navier-Stokes of formule van Poiseuille voor de Franstaligen):
waarin r = straal van de bol is en de rest als hoger. In dit gebied is vooral de viscositeit van belang.
De bol zal versnellen tot het rechterlid van bovenstaande bewegingsvergelijking 0 is. Dan is de eindsnelheid bereikt. Dit zal het geval zijn voor:
Daar de massa evenredig is met r3, betekent dit dat de eindsnelheid, voor zelfde materiaal, evenredig is met r2.
De bewegingsvergelijking is een differentiaalvergelijking met als oplossing:
waarin
Voor lage reynoldsgetallen ligt in het bereikt van 1 to 100 ms. Men kan zien als de tijd die nodig is om 63% van de eindsnelheid te bereiken. In theorie wordt de eindsnelheid pas na een oneindig lange tijd bereikt. 95% van die eindsnelheid wordt echter bereikt na ongeveer 3 x en 99% reeds na 4,61 x . Het is het laatste stukje van het laatste percent dat veel tijd nodig heeft!
2 - Hoge reynoldsgetallen
Bij hoge reynoldsgetallen kan men de tegenwerkende kracht beschrijven als:
waarin
- Cd een coëfficiënt is die experimenteel te bepalen is en afhangt van Re (zie de grafiek supra)
- S = oppervlak van de doorsnede van het voorwerp
- ρ = dichtheid van het medium
De eindsnelheid kan nu geschreven worden als:
Wanneer men weer rekening houdt met het feit dat de massa evenredig is met r3, dan is de eindsnelheid nu evenredig met r1/2.
De bewegingsvergelijking leidt nu tot een differentiaalvergelijking met als oplossing voor de snelheid:
De snelheid als functie van de positie is:
De eindsnelheid wordt nu veel trager bereikt. Voor een voorwerp met een eindsnelheid van 250 km/u wordt 90% van die snelheid pas bereikt na meer dan 560 m.
Voor een vallende persoon ligt de eindsnelheid rond 160 à 180 km/u. Een orkaanwind van boven de 200 km/u kan dus zonder problemen een persoon oppakken en een eindje meevoeren.
In het luchtledige vallen alle voorwerpen even snel. Er is een Youtube filmpje (https://www.youtube.com/watch?v=zzTwoXwtO7E) waarin een astronaut een hamer en een pluim gelijktijdig laat vallen op de maan en beide komen mooi tegelijk op de grond. In een medium (lucht, water ...) echter wordt de valsnelheid bepaald door de verhouding van het gewicht over de weerstand van het medium. Bij zelfde vorm en volume zal een zwaarder voorwerp sneller vallen dan een lichter. Bij gelijk gewicht en verschillende vorm en volume zal een kilogram lood sneller vallen dan een kilogram pluimen.
Bij nog hogere reynoldsgetallen, boven 3.105, treedt er plots een dip op in de weerstandscoëfficiënt, waarbij de weerstand weer evenredig wordt met de snelheid. De tijdconstante is nu echter veel groter. Voor een tennisbal ligt die rond 2 s. Als de bal bij de opslag vertrekt met een snelheid van 180 km/u (= 50 m/s) dan is hij op een halve seconde aan de andere zijde van het terrein (ongeveer 24 m). De bal heeft dan nog ongeveer 78% (e-0.25 x 100) van zijn beginsnelheid. De vertraging is nauwelijks merkbaar. Het donzige oppervlak van een tennisbal en de putjes in een golfbal dienen om de luchtweerstand te verkleinen en nog vroeger in deze dip te komen. De volledige beweging van bv. een golfbal kan niet in één formule worden gevat, maar alleen realistisch worden berekend via numerieke simulatie, waarbij de luchtweerstand kan worden aangepast als functie van de snelheid.
De grafiek van Cd versus Re werd aan de Wiki Commons geschonken door de NASA. Referentie bij de NASA: http://www.grc.nasa.gov/WWW/k-12/airplane/dragsphere.html. Op die bladzijde kan men ook een verklaring vinden voor het geluid dat de wind soms maakt in elektrische draden.
De formule, waarbij de weerstand evenredig is met de snelheid, laat een analytische oplossing voor de differentiaalvergelijkingen toe, zeg maar een pasklare formule voor snelheid en positie in functie van de tijd. Neemt men een klassiek assenkruis met x-as horizontaal en y-as verticaal omhoog, kv de grootte van de weerstand en een bal die vertrekt uit de oorsprong, dan worden de differentiaalvergelijkingen voor de x- en y-as:
In de laatste vergelijking is vy een veranderlijke die zowel positief als negatief kan zijn. Brengt men deze vergelijkingen in een formulering met de D-operator, dan krijgt men:
De algemene oplossing voor de eerste vergelijking is:
Stelt men m/k = en houdt men rekening met de beginvoorwaarde dat vx = vx0 voor t=0, dan kan de integratieconstante C bepaald worden en krijgt men:
De algemene oplossing voor de tweede differentiaalvergelijking bestaat uit een oplossing voor de homogene vergelijking (d.i. met rechterlid = 0) en een oplossing met constante vy:
Wanneer de bal uit stilstand verticaal naar beneden valt, zal de eindsnelheid in de y-richting bereikt worden als er geen versnelling meer is. Uit de differentiaalvergelijking blijkt dat die eindsnelheid vf = mg/k is in grootte. Men noemt de term mg/k in het vervolg vf. De integratieconstante wordt bepaald uit de beginvoorwaarde dat vy = vy0 voor t=0. Men krijgt ten slotte:
Door integreren van de uitdrukkingen voor vx en vy en rekening houdend met de beginvoorwaarden dat voor x=0 en y=0 voor t=0, vindt men:
De lezer kan controleren dat deze vergelijkingen inderdaad voldoen aan de beginvoorwaarden.
Corollarium: de proef van Galilei en van Simon Stevin
[bewerken]Aristoteles beweerde dat voorwerpen des te sneller vallen naarmate ze zwaarder zijn. Deze theorie bleef aanvaard tot in de Middeleeuwen. Er is een verhaal dat Galilei, ergens tussen 1589 en 1592, 2 loden bollen van verschillende diameter en dus verschillend gewicht van de scheve toren van Pisa naar beneden zou gegooid hebben om de theorie te weerleggen. Het verhaal gaat dat beide bollen gelijktijdig de grond bereikten. Er is echter nergens een betrouwbaar verslag hiervan.
De grote wiskundige uit onze streken, Simon Stevin, heeft de proef ook gedaan en daarvan is wel een verslag. Hij liet in Delft 2 loden bollen, de ene 10 maal zwaarder dan de andere, van 30 voet (ongeveer 10 m) naar beneden vallen. Zijn vriend Johan Cornets-de Groot, burgemeester van Delft, hielp hem hierbij. Simon Stevin noteerde dat ze zo gelijktijdig de grond bereikten dat er maar één klop te horen was. Het is niet duidelijk wanneer de proef uitgevoerd werd. Vermoedelijk was het in het jaar 1586. (naar Devreese, J.T. Vanden Berghe, G.: Wonder is gheen wonder.De geniale wereld van Simon Stevin 1548-1620 Davidsfonds, Leuven (België) ISBN: 90-5826-174-3)
Volgens de formules voor de eindsnelheid moet de grote bol een grotere eindsnelheid krijgen dan de kleine bol. Spijtig genoeg wordt nergens vermeld hoe zwaar de bollen waren. Een numerieke simulatie met een loden bol van 10 cm diameter en een van 21,6 cm (2,163 = 10,08) geeft als resultaat dat na 1,5 s ongeveer 11 m afgelegd is en dat het verschil in positie dan nog maar 5 à 6 mm is. Dat valt noch op het gezicht noch op het gehoor als verschil vast te stellen.
Feitelijk is deze proef niet goed bedacht want hij wijzigt 2 parameters tegelijk: het gewicht en de doorsnede van de bollen. Deze parameters hebben daarenboven een tegengestelde invloed. Een betere proef zou zijn om 2 bollen te nemen van dezelfde omvang maar verschillend gewicht, bv. een loden en een houten bol (=0,9 g/cm3). Van alle parameters die een invloed hebben is dan alleen het gewicht verschillend. De simulatie met 2 bollen van 10 cm diameter leert dat na ongeveer 11 m het verschil in positie nog maar 11 cm bedraagt. Zelfs als men de valhoogte opvoert tot rond de 30 m (valtijd = 2,5 s) dan nog is het verschil in positie voor de loden bollen maar 4 cm terwijl het voor de loden en de houten bol reeds 85 cm bedraagt.
De proef van Simon Stevin heeft dus geen correcte conclusies opgeleverd omdat de valhoogte veel te klein was.




























































