Gebruiker:TeunSpaans/Verzamelingen-pdf
Welkom in dit boek over verzamelingen!
Inhoudsopgave
- Inleiding
- I. Wat is een verzameling?
- II. Deelverzamelingen
- III. Basisbewerkingen
- IV. Carthesisch product
- V. Relaties
- VI. Inleiding in de booleaanse logica
- VII. Wetten van de Morgan
- Oplossingen opgaven
- Geschiedenis van de verzamelingenleer
- Bronnen
0 Inleiding
[bewerken]Is dit voor mij?
[bewerken]Wat leer ik in dit boek? Is dit voor mij? Wat heb ik hieraan? Dit hoofdstuk probeert hierop een antwoord te geven.
Dit e-boek leert je wat verzamelingen zijn, waarom ze in de wiskunde belangrijk zijn, en wat je er mee kunt doen. Het is bedoeld voor middelbare school leerlingen en studenten op HBO en universitair niveau. Ook als je je wiskunde weer wilt ophalen, kan dit boek nuttig zijn. Het is niet bedoeld als vervanging van je schoolboeken. Je kunt het wel als aanvulling gebruiken.
In dit boek gaan we in op vragen als:
- wat is een verzameling?
- wat kun je met verzamelingen?
- waarom zijn verzamelingen in de wiskunde belangrijk?
Verzamelingen vormen de basis waarop de wiskunde sinds het begin van de 20e eeuw is opgebouwd. In het hoofdstuk over afbeeldingen zullen we zien hoe we functies en afbeeldingen kunnen definiëren op basis van verzamelingen. Ook getallen worden sindsdien gedefinieerd op basis van verzamelingen. Hiernaast spelen verzamelingen een belangrijke rol in de w:klassieke logica. In het hoofdstuk over deelverzamelingen gaan we hier verder op in.
Opbouw van dit boek:
[bewerken]Elk hoofdstuk bevat een uitleg van de begrippen, en waar mogelijk een formele definitie. De definitie wordt concreet gemaakt met voorbeelden. Van alle belangrijke termen geven we ook de Engelse naam. Het hoofdstuk wordt afgesloten met een aantal oefeningen, waarmee je je de stof kunt eigen maken.
Wat betreft de oefeningen: Maak die! Door de oefeningen te maken, ben je actief met de stof bezig, en maakt je geheugen extra 'paden', extra verbindingen aan naar de plaatsen in je hersens waar de informatie ligt opgeslagen. Door de oefeningen worden de abstracte begrippen ook concreter, je kunt je er meer bij voorstellen. De opgaven beginnen meestal met een eenvoudige overhoring in de vorm van een aantal ja/nee vragen over de theorie uit het hoofdstuk. Deze worden gevolgd door een paar 'reken' opgaven.
Tip: Als je halverwege een hoofdstuk vastloopt, spring dan eens naar de opgaven en maak vast een aantal opgaven, en lees daarna het eerste deel van de theorie nog eens.
Vereiste voorkennis
[bewerken]Er is geen specifieke voorkennis vereist. Het is wel prettig als je vertrouwd bent met abstract denken (al oefen je dat met deze stof ook) door het rekenen met letters, zoals een formule f(x) = 2x + 3. Zulke formules worden soms tot het vak algebra gerekend, al rangschikken anderen het onder de tak van wiskunde die analyse genoemd wordt. Vooral in de voorbeelden zullen we zulke formules herhaaldelijk gebruiken. Als je daar nog niet mee vertrouwd bent, kun je twee dingen doen: of je slaat deze voorbeelden over, en beparkt je tot de voorbeelden van getallen, letters en meetkundige figuren, of je probeert wat over functies te lezen om er in elk geval een basis begrip van te krijgen. Je vindt bijvoorbeeld informatie in het boek Analyse en in het boek Wiskunde/Algebra. Helaas zijn beiden op het moment van schrijven niet af en hebben ook niet de vorm van een leerboek.
Zie ook
[bewerken]Andere plaatsen waar je op wikibooks of wikipedia over verzamelingen kunt leren zijn:
- Basiswiskunde/Getallen/Verzamelingen geeft een kort overzicht van de basis begrippen van de verzamelingenleer.
- w:Verzameling (wiskunde)
- w:Verzamelingenleer gaat dieper in op achtergronden en geschiedenis van de Verzamelingen in de wiskunde.
I Verzamelingen
[bewerken]Na het bestuderen van dit hoofdstuk:
- Heb je een idee van wat verzamelingen in de wiskunde voorstellen
- weet je hoe je een verzameling definieert
- ken je twee bijzondere verzamelingen
- weet je wat de kardinaliteit van een verzameling is
Wat is een verzameling?
[bewerken]Wat is een verzameling? Het begrip Verzameling is de basis waarop het hele gebouw van de wiskunde gebouwd is. Omdat het aan de basis staat, is het niet gedefinieerd uit meer elementaire onderdelen.
De betekenis van het woord verzameling in de wiskunde leunt dicht aan tegen de betekenis van het woord verzameling in het normale spraakgebruik. Ik gewone taal hebben we het bijvoorbeeld over iemands Lego verzameling of zijn verzameling muziek. We hebben het dan over alle Lego blokjes die iemand heeft of over zijn collectie cd’s of MP3’s.
Laten we beginnen met wat voorbeelden van verzamelingen:
- de kleuren van de Nederlandse vlag.
- Alle diersoorten van nu levende diersoorten
- Alle nu levende zoogdierdiersoorten
- Alle regelmatige veelhoeken
- de letters van het alfabet
Tot zo ver voorbeelden uit het dagelijks leven. Maar als wiskundigen zijn we natuurlijk meer geïnteresseerd in voorbeelden met wiskundige zaken zoals getallen:
- Gelijkzijdige driehoek, vierkant, regelmatige vijfhoek, regelmatige zeshoek

- de Natuurlijke getallen 0, 1, 2, 3, …
- De gehele getallen … -3, -2, -1, 0, 1, 2, 3, …
- De rationale getallen 0, 1, 2, ½, 3, 1/3, 2/3 , …
- de reële getallen, dus ook wortel(2), wortel(3), 5 x wortel(2) etc.
- de even getallen
- de waarden Waar en Onwaar
- alle vergelijkingen van de vorm y=ax+b
Definitie
De Duitse wiskundige Georg Cantor definieerde een verzameling als "een collectie van elementen, die volgens een bepaalde definitie bij elkaar horen, en daardoor een geheel vormen".
En als je denkt: "Dat is toch geen lekkere definitie", dan klopt dat helemaal. Want het woord "collectie" is gewoon een synoniem voor het woord "verzameling". Het intuïtieve benaderen van Verzamelingen leidde later tot problemen, wat bleek uit paradoxen zoals de Barbier van Sevilla en de bibliotheek met catalogussen. In het volgende hoofdstuk geven we een verwijzing naar de manier waarop dit probleem in het begin van de 20-ste eeuw werd opgelost.
Notatie
Verzamelingen geven we aan met een Hoofdletter, bijv. A. Voor de elementen in een verzameling gebruiken we een kleine letter, bijvoorbeeld a. Dat een element in een verzameling zit, geven we aan als a A. We spreken dat uit als “a is een element van A” of “a zit in A”.
We noteren een verzameling door de elementen tussen accolades te vermelden. Zolang een verzameling weinig elementen heeft, kunnen we ze gewoon opsommen. Bijvoorbeeld de verzameling van de kleuren van de Nederlandse vlag kunnen we weergeven als { rood, wit, blauw}.
Zoals je ziet worden de elementen van de verzameling gescheiden door een komma.
Wanneer het aantal elementen groot wordt, werkt dat natuurlijk niet meer. Bij A={a, b,c,d,e,f,g,h,i,j,k,l,m,n,o,p,q,r,s,t,u,v,w,x,y,z} is dat nog te doen, maar in het voorbeeld van de zoogdiersoorten wordt het te groot. En dat is nog afgezien van de vraag of alle soorten zoogdieren bekend zijn, of dat er nog onbekende zoogdiersoorten op onze planeet bestaan.
In een aantal gevallen kunnen we dat oplossen door met puntjes te werken. Met {1, 2, 4, 8, 16, 32, 64, ...} geven we aan dat de serie oneindig doorloopt. We kunnen dat ook doen als de serie beperkt is. Bijvoorbeeld de letters van het alfabet V={a, b, c, ..., y, z}.
Voor echt grote verzamelingen kunnen we een verkorte notatie gebruiken:
- A = {alle diersoorten x : waarvoor geldt dat x is levendbarend en de jongen worden gezoogd}
- We spreken dit uit als: A is de verzameling van alle diersoorten x, waarvoor geldt dat x levendbarend en de jongen worden gezoogd.
Alternatieve notatie: In plaats van ":" wordt ook "|" gebruikt.
Als we willen zeggen dat a en b elementen van de verzameling L = letters zijn, noteren we dat als L en L
Of een wiskundig voorbeeld:
- V={3x:x} komt overeen met de verzameling {3, 6, 9, 12, ...}
2 restricties
- De volgorde waarin elementen worden opgesomd is niet belangrijk. Een verzameling bestaat uit zijn elementen en niets anders. Als een verzameling A bestaat uit de elementen 1, 2 en 4 en verzameling B bestaat uit de elementen 4, 2 en 1, dan zijn beide verzamelingen hetzelfde. We schrijven dan A = B. Het is wel de gewoonte om elementen, als het getallen zijn, van klein naar groot te noteren.
- We noemen elementen ook maar 1 maal bij de definitie van een verzameling, een verzameling bevat dus nooit twee identieke elementen. Dus een verzameling met de elementen {1, 2, 2, 3, 3} schrijven we gewoon als {1, 2, 3}.
Bekende verzamelingen
[bewerken]Voorbeelden van getallenverzamelingen zijn:
- De natuurlijke getallen stellen gewoon aantallen voor: 0, 1, 2,3 etc. Deze verzameling wordt aangegeven met de letter .
- De gehele getallen bevatten naast de natuurlijke getallen ook de negatieve getallen”: … -3, -2, -1, 0, 1, 2, 3, … Deze verzameling wordt weergegeven met de letter .
- De rationale getallen, die bestaan uit de gehele getallen en de w:Breuk (wiskunde):breuken. Deze verzameling geven we aan met de letter .
- De Algebraische getallen, die bestaan uit de oplossingen van de polynomen: ax+b=0, ax2+bx+c=0, a1x3+a2x2+a3x+a4=0, etc. Hieronder vallen dus alle tweede en derde machtswortels.
- De reële getallen, waaronder ook de transcendente getallen vallen. Deze verzameling geven we aan met de letter
- De complexe getallen verschijnen als oplossing van vergelijkingen als . Deze verzameling geven we aan met de letter .
Let op de dubbele streep in de letters die de naam aangeven.
De Lege Verzameling
[bewerken]Een bijzondere verzameling is de verzameling ={}: de lege verzameling. De lege verzameling heeft geen elementen. Spreek de naam uit als 'fie'. Nu denk je misschien: wat kan ik met die lege verzameling? Maar dat is heel wat. Die blijkt heel essentieel voor de opbouw van de wiskunde. We komen daar verderop in dit Hoofdstuk, onder het kopje kardinaliteit, op terug.
De Universele verzameling
[bewerken]Voor we aan de bewerking gaan beginnen die Vereniging genoemd wordt, is het nuttig eerst iets te definiëren dat we Universele verzameling noemen. Wanneer we over verzamelingen praten, doen we dat meestal in een bepaalde context, in een bepaald verband. Dat verband noemen we in de verzamelingenleer het Universele verzameling en geven we aan met de letter U.
Laten we het verduidelijken met een aantal voorbeelden.
- Wanneer we het hebben over een verzameling letters, doen we dat meestal in het verband van de letters van het alfabet. Ons Universele verzameling is dan U={a, b, c, d, e, f,
g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z}. Het is goed om altijd het Universele verzameling duidelijk te benoemen. Voor de letters kun je ook kiezen voor alle letters die in de Arial tekenset zitten. Die verzameling is uitgebreider dan de 26 letters van het alfabet.
- Wanneer we praten over rechte lijnen, kunnen we als ons Universele verzameling de verzameling van alle rechte lijnen kiezen. Definitie: U={f(x): f(x) = ax+b , met a, x en b reële getallen }
Het Universele verzameling is zelf een verzameling, en net als de lege verzameling is het een bijzondere verzameling die we vaak zullen tegenkomen.
Kardinaliteit
[bewerken]De kardinaliteit is het aantal elementen in een verzameling. De kardinaliteit van is 0. De kardinaliteit van {Zwart, Geel, Rood} is 3. De kardinaliteit van de verzameling Natuurlijke getallen is oneindig, meer precies aftelbaar oneindig. Dat geldt ook voor de verzameling en . We noteren de kardinaliteit van een verzameling A als : |A|.
Hierboven hadden we het over de lege verzameling . Die kunnen we gebruiken om andere verzamelingen met te bouwen.
- is gewoon de lege verzameling
- {} is een verzameling met 1 element, namelijk de lege verzameling. We hebben dus een verzameling met als element een andere verzameling!
- {{}} is een verzameling met 1 element, namelijk de verzameling met als enige element de lege verzameling. We halen dus eigenlijk bovenstaande trucje nog een keer uit en krijgen zo een tweede verzameling.
- {{{}}} is een verzameling met 1 element, namelijk de verzameling hierboven.
In de inleiding schreven we dat in de wiskunde de getallen gedefinieerd konden worden aan de hand van verzamelingen. Dat werkt ruwweg als volgt:
- 0 = de kardinaliteit van de lege verzameling = ||.
- 1 = de kardinaliteit van de verzameling {} (dus de verzameling met als enige element de lege verzameling ) = |{}|
- 2 = de kardinaliteit van {, {}} = |{, {}}|
- 3 = de kardinaliteit van {, {}, {{}}} = |{, {}, {{}}}|
etc.
Oneindig
[bewerken]Wat is de kardinaliteit van ? We noemen die oneindig. Maar wat is oneindig? Is oneindig altijd hetzelfde of zijn daar nog gradaties in? Daarover gaat dit stukje. We zagen hierboven dat er behalve de natuurlijke getallen ={1, 2, 3, 4,5 5, ...} ook een verzameling voor de gehele getallen is. Heeft meer getallen dan ?
Het hangt er een beetje vanaf hoe je telt, maar we noemen twee verzamelingen gelijkmachtig als we er een 1:1 afbeelding tussen kunnen definiëren. We noemen de kardinaliteit van N (alef nul).
we kunnen eenvoudig een 1:1 afbeelding tussen en definiëren. Namelijk:
- 0-->0
- 1-->1
- -1-->2
- 2-->3
- -2-->4
etc.
Het blijkt dat we ook een 1:1 afbeelding tussen en kunnen definiëren. Dat kan als volgt:
Maar het kan ook meer visueel:

Dit geldt ook voor de algebraïsche getallen , als is dat wat lastiger te illustreren. We noemen zowel , als aftelbaar oneindig. Pas bij de reëel getallen gaat dit niet meer op. Die heeft een andere graad van oneindig, en die nomen we overaftelbaar oneindig.
Engelse namen
[bewerken]- Verzameling: Set of Class
- Element: Element
- Natuurlijke getallen: Natural numbers
- Gehele getallen: Integers
- Reële getallen: Real Numbers
- Complexe getallen: Complex numbers
- Kardinaliteit: Cardinality
- Universele verzameling: Universe (soms Universe of Discourse genoemd). Omdat de universele verzameling in het Engels Universe wordt genoemd, en ook omdat Universum korter is, gebruiken we in het Nederlands ook wel het woord Universum in plaats van Universele verzameling.
Opgaven
[bewerken]- I.1) Geef van de volgende beweringen aan of ze goed of fout zijn:
- i) Verzamelingen en elementen zijn hetzelfde
- ii) Een verzameling heeft altijd minstens 1 element
- iii) Een verzameling kan andere verzamelingen als element bevatten
- iv) Bij elke element in een Universele verzameling is een verzameling te bedenken waar dit element in zit
- v) A={x:x } bevat alle breuken
- vi) A={x:x=a/b met a,b} bevat alle breuken
- I.2) Schrijf op twee manieren de verzameling klinkers
- I.3) Schrijf de kleuren van de Belgische vlag als verzamelingen
- I.4) Zonder in de stof hierboven te spieken, schrijf de namen van de belangrijkste verzamelingen van getallen op.
- I.5) Hoe zou je de verzameling even getallen definiëren?
- I.6) Wat is de kardinaliteit van de verzameling {0, 1, 2, 3, 4}?
- I.7) Wat is de kardinaliteit van de complexe getallen?
- I.8) Schrijf de verzameling met de kleuren Blauw, Rood en Wit op zo veel mogelijk verschillende manieren.
Samenvatting: Wat heb je geleerd?
- Je weet wat verzamelingen voorstellen.
- Je weet dat je een verzameling noteert als {x:voorwaarde(n) waaraan x voldoet} of als {opsomming van elementen}
- Je kent twee bijzondere verzamelingen, en het Universele verzameling U.
- Je weet dat de kardinaliteit het aantal elementen van een verzameling is en dat je die noteert als |V|
II Deelverzamelingen
[bewerken]Na het bestuderen van dit hoofdstuk:
- Weet je wat een deelverzameling is
- Ken je de verschillende notaties voor deelverzameling
- Weet je wat een machtsverzameling is
- Weet je wat een partitie is
Deelverzameling
[bewerken]We zagen in het vorige hoofdstuk dat een Verzameling uit elementen bestaat. Laten we als voorbeeld een eindige verzameling nemen L die bestaat uit de letters van het alfabet zoals we dat in Nederland en België kennen. L={a,b,c,d,e,f,g,h,i,j,k,l,m,n,o,p,q,r,s,t,u,v,w,x,y,z} Stel dat we vanuit bovengenoemde L :
- A={a,b,c}
- E={a,b,c,d,e}
- K={a,e,i,o,u}
- Z={x,y,z}
- Y={v,w,x,y,x}
Omdat alle elementen van A in L voorkomen, noemen we A een deelverzameling van L Hetzelfde geldt voor de hier genoemde verzamelingen E, K, Z en Y. We noteren dat als A ⊂ L of We zeggen dan “A is een deelverzameling van L”.

De notatie A ⊆ L wordt gebruikt om aan te geven dat A een deelverzameling is van L, maar niet noodzakelijk een echte deelverzameling.
Helaas gebruiken niet alle auteurs hier dezelfde betekenis.
- Sommige schrijvers gebruiken A ⊂ B om aan te geven dat A een deelverzameling van B is, en niet noodzakelijk een echte deelverzameling. Ze gebruiken dit symbool om zowel echte als niet echte deelverzamelingen aan te geven.
- Een tweede groep gebruikt Anderen gebruiken A ⊂ B om aan te geven dat A een echte deelverzameling van B is. Ze gebruiken A ⊆ B als deelverzameling A gelijk kan zijn aan B.
- Een derde groep wiskundigen gebruikt A ⊆ B om aan te geven dat A een deelverzameling is van B, maar niet noodzakelijk een echte deelverzameling. Ze gebruiken A ⊊ B om een echte deelverzameling aan te geven.
In dit document gebruiken we zo veel mogelijk:
- A ⊆ B om aan te geven dat A een deelverzameling is van B, maar niet noodzakelijk een echte deelverzameling. Omgekeerd kunnen we dit schrijven als B ⊇ A.
- A ⊊ B om aan te geven dat A een echte deelverzameling is van B. We kunnen dit ook omgekeerd schrijven als B ⊋ A. Let op de streepjes door lage horizontale streep.
Voorbeelden:
- In bovenstaande voorbeeld geldt: A ⊊ L, E ⊊ L, K⊊ L, Y⊊ L en Z ⊊ L
- Z ⊊ Y ⊊ L oftewel Z is bevat in Y is bevat in L.
- ⊊
- ⊊
De lege verzameling wordt als deelverzameling van elke verzameling gezien.
Machtsverzamelingen
[bewerken]De machtsverzameling van een verzameling is de verzameling van alle deelverzamelingen.
- Voorbeeld 1: Laat B={a,b}
Dan is de machtsverzameling (B) = {{}, {a}, {b}, {a,b}}. De kardinaliteit van deze machtsverzameling is 2^2=4.
- Voorbeeld 2: in bovenstaande Z={x,y,z} is de machtsverzameling P(Z) = {A:A ⊆ Z}
(Z)= {{}, {x}, {y}, {z}, {x,y), {x,z}, {y,z}, {x,y,z}}. Merk op dat de kardinaliteit van deze machtsverzameling 2^3=8 is. De kardinaliteit van een machtsverzameling van ene verzameling met n elementen is 2^n. Hiervan is het woord machtsverzameling afgeleid. We gaan deze formule hier niet bewijzen, dat valt onder het hoofdstuk w:combinatoriek.
Partities
[bewerken]Wanneer we alle elementen van een verzameling over een aantal deelverzamelingen verdelen, spreken we van een ‘’partitie’’. In een partitie hebben we verschillende deelverzamelingen, die samen alle elementen van de oorspronkelijke verzameling bevatten, zonder dat een element dubbel voorkomt of weggelaten wordt.
Als plaatje een voorbeeld:

Het linker vakje bevat de elementen a en b. Het middelste vakje bevat het element c. Het rechter vakje bevat de elementen d en e.
Voorbeeld 2:
- Laat V={a, b, c}. Dan is {{A}, {b,c}} een partitie van V.
We zetten de eisen aan een partitie nog even op een rijtje:
- Een partitie van een verzameling V bestaat uit deelverzamelingen van V
- Elk element van V komt in een van de elementen van de partitie.
- De deelverzamelingen in de partitie bevatten alleen elementen uit V
Daarnaast spreken we af dat de lege verzameling geen deel is van de partitie
Stellingen
[bewerken]- Als A ⊆ B en B ⊆ A dan A=B . (stelling 2.1)
- Omgekeerd geldt dat als A=B dan A ⊆ B en B ⊆ A (stelling 2.2)
- Als a ∈ A en A ⊆ B, dan a ∈ B. (stelling 2.3)
- Als A ⊆ B en B ⊆ C, dan A ⊆ C. (stelling 2.4)
Bewijs van nr 1: Als A ⊆ B wil dit zeggen dat alle elementen van A in B zitten. Omgekeerd wil B ⊆ A zeggen dat alle elementen van B in A zitten. Kortom, de elementen van beide verzamelingen zijn gelijk, wat de definitie is van gelijke verzamelingen.
De andere 2 bewijzen komen voor als opgave.
Deelverzamelingen en Klassieke logica
[bewerken]Deelverzamelingen vormen de basis van wat vroeger als de Klassieke Logica of Aristotelische Logica werd beschouwd, hoewel John Baez terecht schreef dat Deelverzamelinglogica een betere naam is dan Klassieke logica.
Ons instrumentarium is op dit moment voldoende om twee vormen te beschrijven.
vorm 1
[bewerken]Laat a een element van verzameling A zijn, dus aA. Laat A ⊆ B. Dan is a niet alleen een element van A, maar ook van B. (stelling 2.3 hierboven)
Geïllustreerd:
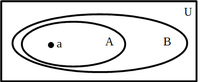
- Voorbeeld 1: Jan is veeboer, en alle veeboeren zijn boeren. Is Jan een boer?
- Laat veeboeren een verzameling zijn. Omdat alle veeboeren boeren zijn, is veeboeren een deelverzameling van boeren. Jan is element van de verzameling veeboeren, deelverzameling van de verzameling boeren, dus Jan is een element van de verzameling boeren.
- Voorbeeld 2: Een hamer is een stuk gereedschap. Alle gereedschappen zijn door mensen gemaakt. Wat kunnen we over een hamer zeggen?
- Laat gereedschappen verzameling A zijn. Laat door mensen gemaakte voorwerpen verzameling B zijn. A is een deelverzameling van B. Hamer is een element van A. Dus hamers zijn door mensen gemaakt.
Dit geldt voor alle punten a A. Elke keer als we dit in onze omgeving tegenkomen, weten we dat deze afleiding juist is. We hoeven dat niet elke keer opnieuw te beredeneren.
vorm 2
[bewerken]Bekijk de zinnen:
- alle aanhangers van Socrates zijn filosofen
- alle filosofen zijn mensen
- alle mensen zijn sterfelijk
We herkennen in bovenstaande zinnen drie verzamelingen: A={aanhangers van Socrates}, B={filosofen}, C={mensen} en D={sterfelijke wezens}. De drie zinnen komen dan neer op:
- A ⊆ B
- B ⊆ C
- C ⊆ D
Door herhaaldelijk stelling 2.4 te gebruiken, kunnen we concluderen dat A ⊆, en dus alle aanhangers van Socrates sterfelijk zijn.
In een Venn-diagram wordt dat weer heel duidelijk geïllustreerd:

Beide vormen zijn heel elementair, en in het volgende hoofdstuk gaan we hier verder op in en kijken we ook naar ingewikkelder situaties.
Engelse termen
[bewerken]- deelverzameling: subset
- machtsverzameling: powerset of kortweg poset
- partitie: partition
Opgaven
[bewerken]- II.1) Geef aan of de volgende beweringen juist of onjuist zijn:
- 1.i) Elke verzameling is een deelverzameling van zijn Universele verzameling U.
- 1.ii) Elke verzameling is een deelverzameling van
- 1.iii) De Machtsverzameling van {a, b, c, d} heeft 16 elementen
- 1.iv) Als A={1, 2, 4}, B={3, 7, 8} en C={5, 6, 9, 10} dan is dit een partitie van {1 2, 3, 4, 5, 6, 7, 8, 9, 10}
- II.2) Als Betsy een koe is, en alle koeien in de wei staan, waar staat Betsy dan?
- II.3) Als Jan een loodgieter is, en alle loodgieters verantwoordelijk werk doen, wat kunnen we dan over Jan zeggen?
- II.4) Dagpauwogen zijn vlindersoorten. Alle vlindersoorten zijn insecten. Wat kunnen we zeggen over dagpauwogen?
- II.5) Beredeneer de waarheid van stelling 3.
- II.6) Beredeneer de waarheid van stelling 4.
Samenvatting: In dit hoofdstuk heb je geleerd
- Wat een deelverzameling is
- Hoe je een deelverzameling noteert (A ⊆ B)
- Wat een machtsverzameling is en hoeveel elementen die bevat
- Wat een partitie is
III Basisbewerkingen
[bewerken]Na het bestuderen van dit hoofdstuk:
- Weet je wat doorsnede van twee verzamelingen is
- Weet je wat de vereniging van twee verzamelingen is
- Weet je wat het complement van een verzameling is.
- Weet je hoe je twee verzamelingen kunt aftrekken.
Basisbewerkingen van en Operaties op verzamelingen
[bewerken]In het vorige hoofdstuk hebben we gezien wat een deelverzameling is en wat we er mee kunnen doen. In dit hoofdstuk kijken we naar 3 bewerkingen op verzamelingen: De doorsnede, de vereniging en het complement. We gebruiken Venn-diagrammen als illustratie.
Doorsnede
[bewerken]
De doorsnede van twee verzamelingen is een verzameling met de elementen die in beide verzamelingen voorkomen. We noteren de doorsnede met het ∩ teken.
Voorbeeld:
- Als A={1,2,3,4,5} en B={4,5,6,7,8}, dan bestaat de doorsnede A B = {4,5}
Definitie:
Andere voorbeelden zijn:
- Als B={de kleuren van de Belgische vlag}={Geel, Rood, Zwart} en D={de kleuren van de Duitse vlag} dan BD = B=D.
- Als A={a,b,c} en B={ x,y,z} dan AB =
- Als en , dan
- Laat . Laat . Dan bestaat uit het kruispunt van de twee lijnen.
De Doorsnede heeft een aantal overeenkomsten met het optellen bij gewoon rekenen in :
Eigenschap Rekenen Doorsnede Gesloten Als a en b natuurlijke, gehele, rationele of reële getallen zijn,
dan is a+b een natuurlijk, geheel, rationaal of reëel getalAls A en B verzamelingen zijn, dan is A ∩ B ook een verzameling. Commutatief a + b = b+a A ∩ B = B ∩ A Associatief a + (b + c) = (a +b ) + c A ∩ (B ∩ C) = (A ∩ B) ∩ C Neutraal element of 0-element a + 0 = a voor alle a A ∩ U = A voor alle A Inverse bewerking Voor alle a is er een invers element b zodat a+b = 0 Voor deze eigenschap kent de doorsnede geen overeenkomst
In de tak van wiskunde die w:Groep (wiskunde):Groepentheorie genoemd wordt, wordt een set verzamelingen met de doorsnede bewerking als een (abelse) semi-groep gezien.
Vereniging
[bewerken]
De tegenhanger van de doorsnede is de Vereniging. Wanneer we 2 verzamelingen A en B hebben, dan bevat de vereniging A ∪ B van die twee verzamelingen alle elementen die in A zitten, en daarbij alle elementen die in B zitten, en natuurlijk dus ook alle elementen die in de doorsnede A
Voorbeelden:
- Als A={a, b, c} en B={c, d, e}.
- Dan is A ∪ B = {a, b, c, d, e}
- Als A={y(x):y(x)=ax+b} en B={f(y):x(y)=c}, dan bevat A alle lijnen in het platte vlak met uitzondering van de vertikale lijn, en B bevat alle vertikale lijnen. De vereniging bevat dan alle lijnen in het platte vlak.
Definitie
- A ∪ B = {x:x A of x B}
We kunnen hier een zelfde tabel opstellen als bij de doorsnede.
Eigenschap Rekenen Vereniging Gesloten Als a en b natuurlijke, gehele, rationele of reële getallen zijn,
dan is a+b een natuurlijk, geheel, rationaal of reëel getalAls A en B verzamelingen zijn, dan is A ∩ B ook een verzameling. Commutatief a + b = b+a A ∪ B = B ∪ A Associatief a + (b + c) = (a +b ) + c A ∪ (B ∪ C) = (A ∪ B) ∪ C Neutraal element of 0-element a + 0 = a voor alle a A ∪ = A voor alle A Inverse bewerking Voor alle a is er een invers element b (namelijk -a) zodat a+b = 0 Voor deze eigenschap kent de vereniging geen overeenkomst
Complement
[bewerken]De derde basisbewerking is het complement.
Definitie: Het Complement van een verzameling A bestaat uit alle elementen uit het Universele verzameling U die niet in de verzameling A zitten.. We noteren het complement als : of . Er is geen verschil in betekenis tussen en , het zijn gewoon twee verschillende notaties voor een en hetzelfde begrip.
Meer wiskundig geformuleerd:
Voorbeelden:
- U={0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, oftewel de verzameling van alle cijfers. Stel A={1, 2, 3}. Dan = {0, 4, 5, 6, 7, 8, 9}}
In een Venndiagram:

.
Eigenschappen
[bewerken]Het complement van het complement van een verzameling is de verzameling zelf:
- (stelling 3.1)
Samen met het complement vormt een verzameling de hele universele verzameling:
- (stelling 3.2)
Een verzameling heeft geen gemeenschappelijk element met zijn complement:
- (stelling 3.3)
'Buiten' de universele verzameling is niets:
- (stelling 3.4)
- (stelling 3.5)
Verschil
[bewerken]De Vereniging van verzamelingen lijkt ogenschijnlijk wel wat op optellen, al is het duidelijk dat er verschillen zijn. Zo is bijvoorbeeld het aantal elementen in A ∪ B niet per definitie hetzelfde als de som van het aantal elementen in A + het aantal elementen in B.
Toch bestaat er een operatie die we 'aftrekking' noemen.

Definitie
- B-A=(x:xB en xA}
Voorbeelden
- Laat A={1, 2, 3, 4, 5} en B={4 , 5, 6, 7, 8, 9}. Dan is B-A={1, 2, 3}
- Laat A={(x,y): y=ax^2+bx+c} en B={(x,y):y=dx=e}. Dan bestaat A-B uit de verzameling 'echte' parabolen, A-B={(x,y): y=ax^2+bx+c met a ongelijk 0}
Toepassingen
[bewerken]De Engelse wiskundig Charles Ludwig Dodgson, beter bekend als w:Lewis Carroll, schreef behalve verrukkelijke kinderboeken ook wiskundige boeken. Hij verzamelde een groot aantal problemen in boeken als "Symbolic Logic" en "The game of Logic". We zullen er hier enkele beschrijven, omdat deze met verzamelingen kunnen worden opgelost.
Voorbeeld
a. Geen vette dieren rennen goed
b. Sommige hazewindhonden rennen goed
Wat kunnen we hier uit concluderen?
Hoe pakken we dit aan?
We zien 3 verzamelingen, die we hierbij gelijk met een letter aangeven. V=Vette dieren, G=Goede renners, H=hazewindhonden.
De eerste bewering (a.) zegt dat de verzamelingen V en G disjunct zijn, dus een lege doorsnede hebben.
De tweede bewering (b.) zegt dat de doorsnede van G en H niet leeg is.
Laat x een element van de doorsnede van G en H zijn. Omdat x dan element van G is, en G en V geen gemeenschappelijke elementen hebben, is x dus geen element van V. Terugvertaald naar onze vraag: Sommige hazewindhonden zijn niet vet.
Zie de opgaven voor meer van zijn problemen.
Engels
[bewerken]- Doorsnede: Intersection
- Vereniging: Union
- Complement: Complement
- Verschil: Difference
Opgaven
[bewerken]- III.1 Geef van de volgende beweringen aan of ze waar of niet waar zijn:
- III.1.i) De Universele verzameling U heeft complement
- III.1.ii) De Universele verzameling U heeft geen complement
- III.1.iii) De leger verzameling is zijn eigen complement
- III.1.iv) Als twee verzamelingen A en B disjunct zijn, is de doorsnede
- III.1.v) Als een element e geen element is van A, die deel is van Universele verzameling U, dan is e Ac
- III.2 Schrijf de volgende verzamelingen uit in de vorm {element 1, ... , element n}
- III.2.i) Als A= {1, 2, 3, 4, 5} en B={2, 4, 6, 8}, wat is dan A ⋂ B?
- III.2.ii) Als A= {1, 2, 3, 4, 5} en B={2, 4, 6, 8}, wat is dan A ⋃ B?
- III.2.iii) Als A= {1, 2, 3, 4, 5} en B={2, 4, 6, 8}, wat is dan A-B?
- III.2.iv) Als A= {1, 2, 3, 4, 5} en B={2, 4, 6, 8}, wat is dan A\B?
- III.2.v) Als A= {1, 2, 3, 4, 5} en de Universele verzameling is , wat is dan Ac?
- II.3) Schrijf minstens 3 deelverzamelingen van {Geit, Varken, Koe, Kip} op.
- II.4) Wat is de vereniging van {do, re, mi} en (bas, tenor}?
- II,5) Wat zijn de elementen van {Koe, kip, kat, kariboe, krokodil} - {kip, kariboe, kat, koala, kolibri}?
- III.6
Sommige vakanties zijn regenachtig.
Regenachtige dagen zijn vermoeiend.
Wat kun je hieruit concluderen?
- III.7
Geen oude konijnen zijn egoïstisch
Alle zwarte konijnen zijn egoïstisch
Wat kun je hieruit concluderen?
- III.8
Babies zijn onlogisch
Niemand die een krokodil aankan, wordt veracht
Onlogische personen worden veracht
Wat kun je hieruit concluderen?
Samenvatting: In dit hoofdstuk heb je geleerd dat:
- de doorsnede van twee verzamelingen (A ∩ B) bestaat uit de elementen die in zowel A als B voorkomen
- de vereniging van twee verzamelingen (A ∪ B) bestaat uit de elementen die in minstens 1 van de twee verzamelingen voorkomen.
- het Complement van een verzameling bestaat uit de elementen die niet in verzameling A voorkomen. We noteren het Complement als AC
- Het verschil van 2 verzamelingen A-B bestaat uit de elementen die wel in A maar niet in B zitten.
IV Carthesisch product
[bewerken]Na het bestuderen van dit hoofdstuk:
- Weet je wat het Cartetisch product van twee verzamelingen is
- Kun je zelf het product van twee verzamelingen samenstellen
Carthesisch product
[bewerken]In het vorige hoofdstuk zagen we hoe we met de doorsnede, de vereniging en het verschil van twee verzamelingen nieuwe verzamelingen konden maken. In dit hoofdstuk komen we nog een manier tegen: het product van twee verzamelingen.
Stel we hebben twee verzamelingen A en B. Dan definiëren we het product van die twee verzamelingen als :
- A X B = {(a,b):aA en bB}
Of in gewoon Nederlands: als we twee verzamelingen A en B hebben, dan bestaat het product uit alle verschillende paren elementen van die twee verzamelingen.
Voorbeeld 1:
- Laat A={1, 2, 3) en B={5, 6}
- Dan A X B = {(1,5), (1,6), (2, 5), (2,6), (3,5), (3,6)}
- En B X A = {(5,1), (5,2) (5,3) (6,1), (6,2) (6,3)}
Voorbeeld 2:
- x = verzameling van alle roosterpunten in het platte vlak.
Eigenschappen
- Voor eindige verzamelingen A en B geldt duidelijk dat:| A X B | = | A | x | B |. Immers bij de paren (a, b) hebben we voor a |A| mogelijkheden en voor b hebben we |B| verschillende mogelijkheden.
- In het eerste voorbeeld zien we dat A x B niet hetzelfde is als B X A. De commutatieve eigenschap die we bij het vermenigvuldigen van getallen kennen (2 x 3 = 3 x 2), gaat hier dus niet op.
- A X = = X A, oftewel als een van de te vermenigvuldigen verzamelingen leeg is, dan is het product ook leeg.
- Het Cartesisch product is evenmin associatief: (A X B) X C ≠ A X (B X C)
- Merk op dat X het platte vlak geeft.
A x A
[bewerken]Wanneer we het product van een verzameling A met zichzelf nemen, zoals A X A, dan schrijven we dit ook als A2.
Generalisatie
[bewerken]Natuurlijk kunnen we dit generaliseren. Wanneer we 3 verzamelingen A, B en C hebben, dan kunnen we praten over A X B X C = {(a,b,c)|aA, bB, cC}
En nog verder: A1 X A2 X A3 ... X An = An = {(a1, a2, a3, ... an)|a1 A1, a2 A2, a3 A3, ... an) An}.
Engels
[bewerken]- Carthesisch product : Cartesian product
Opgaven
[bewerken]- Zijn de volgende beweringen Waar of Onwaar?
- IV.1.i) Het Cartesisch product van A={1} X heeft geen elementen
- IV.1.ii) | A={1} X | = 1
- IV.1.iii) Het Cartesisch product van A={1} X B={a,b} = {(a,1), (b,1)}
- IV.2a Als A={a, b} en B={3,4}, schrijf dan de elementen op van A X B.
- IV.2a Als A={a, b} en B={3,4}, schrijf dan de elementen op van B X A.
- IV.3a Als L={Waar, Onwaar}, wat zijn dan de elementen van L2?
- IV.3b Als L={Waar, Onwaar}, wat is dan de kardinaliteit van L2?
- IV.3c Als L={Waar, Onwaar}, wat is dan de kardinaliteit van L3?
- IV.3d Wat denk je dat de algemene formule is voor de kardinaliteit van Ln als L={Waar, Onwaar}?
- IV.4 Schrijf alle elementen op van L3 als L={W, O}
Samenvatting: In dit hoofdstuk heb je geleerd dat:
- wat het product van twee verzamelingen is
- hoe je dit zelf kunt samenstellen
V Relaties
[bewerken]Na het bestuderen van dit hoofdstuk:
- Weet je wat een afbeelding is
- Weet je wat een operator is
- Weet je wat een relatie is
- weet je wat een equivalentieklasse is
- weet je wat een partiele ordening is
Relaties
[bewerken]Met een relatie bedoelen we een verband (de relatie) tussen 2 verzamelingen.
Voorbeeld:

Afb. 5.1
Vaak worden relaties gedefinieerd op basis van gemeenschappelijke eigenschappen of kenmerken. De wiskundige en logicus De Morgan, die we in het vorige hoofdstuk tegen kwamen, definieerde relaties als:
- "When two objects, qualities, classes, or attributes, viewed together by the mind, are seen under some connexion, that connexion is called a relation."
of in het Nederlands:
- Wanneer twee objecten, kenmerken, attributen, of klassen samen beschouwd worden, en hier een verband gezien wordt, dan wordt dat verband een relatie genoemd.
Merk op dat hier strikt genomen enkel op tweeplaatsige relaties gedoeld wordt.
Tegenwoordig gebruiken we een exactere definitie: Een relatie R tussen een aantal verzamelingen A1, A2 ... An definiëren we als een aantal n-tupels (rijen) (a1, a2, ... an) waarin a1 A1 etc. Zo'n rij is een element van van het cartesisch product A1> X A2 X ... X An is dan een element van de verzameling R.
Illustratie:

We kunnen tussen deze twee verzamelingen 3 voor de hand liggende relaties definiëren. We illustreren twee hiervan:

De linker relatie is gelegd op grond van de vorm (driehoek met driehoek, etc), de rechter is gelegd op grond van de vulling van het vlak.
Afb. 5.2
Opgave
Kun je zelf de 3e relatie schetsen?
Het aantal verzamelingen noemen we de plaatsigheid van een relatie.
Sommige wiskundigen gaan nog een stap verder in het formaliseren. We schreven hierboven dat een relatie bestaat uit een aantal n-tuples op het cartesisch product van n- verzamelingen. Sommigen noemen deze verzameling n-tuples G en definiëren een relatie R als bestaande uit G en het cartesisch product, dus R={G, A1, A2 ... An}. Het verschil is wat theoretisch semantisch, maar met beiden wordt hetzelfde bedoeld. Zo volgt de Engelstalige wikipedia in haar artikel de definitie wara we mee begonnen, terwijl de Nederlandstalige wikipedia in het artikel over relaties de laatste vorm kiest.
Er zijn 3 soorten relaties die we bijzonder aandacht geven:
Deze 3 soorten relaties worden in dit hoofdstuk hierna verder uitgewerkt.
Afbeeldingen
[bewerken]Een afbeelding is een vorm van een relatie, zoals hierboven beschreven. Het verschil is dat een afbeelding een richting heeft. Wanneer we met getallen werken, gebruiken we het woord functie.
Grafische illustratie van een afbeelding:

Afb. 5.3
De linker verzameling heeft 3 elementen, de letters a, b en c, de rechter 2, namelijk de cijfers 1 en 2. De afbeelding beeldt a en b op 2 af, en de letter c op 1.
De 'van' verzameling A wordt het domein genoemd, de 'naar' verzameling B wordt het codomeinof Bereik genoemd. We spreken van een afbeelding in als er elementen in B zijn waarop geen enkel element van A wordt afgebeeld, en van afbeelding op als er voor alle elementen in B een element van A bestaat dat hierop wordt afgebeeld. In dit geval wordt met het bereik de verzameling waarden van f(x) bedoeld, dus het bereik=:F(x)|xA}.
Definitie:
Een afbeelding F van verzameling A naar verzameling B is een deelverzameling van het Cartesisch product A X B. De paren zijn geordend. Hierbij geldt
- (a) Een afbeelding gaat altijd naar 1 element van het bereik.
- (b) meerdere elementen uit het domein mogen worden afgebeeld op 1 element van het bereik.
Notatie: Een afbeelding F van A naar B wordt genoteerd als:
of ook als
of als
- f=(G, A, B) waarbij G de verzameling geordende paren is.
Wanneer we het over afbeeldingen met getallen hebben, spreken we meestal over functies.
meerplaatsige afbeeldingen
Bovenstaande definitie gaat uit van een tweeplaatsige afbeelding. We kunnen meerplaatsige functies definiëren, bijvoorbeeld een functie
Voorbeelden van afbeeldingen:
- Laat A = B =. Definieer f(x)=2x+3.
- Laat A={Verzameling geometrisch figuren}, en B=. Definieer f(x) als {f(x):aantal rechte lijnstukken van x waarbij xA}
- Laat A={Verzameling driehoeken}, en B=. Definieer f(x) als f(x)=de oppervlakte van driehoek x.
- f(x)=3x
- f(x)=sin(x)/x
Operatoren
[bewerken]Bij het gewone rekenen kennen we operaties als optellen, aftrekken, vermenigvuldigen, delen, machtsverheffen en worteltrekken. We noemen de "+", "-", "x" en "/" operatoren. Met bovenstaande kennis kunnen we nu zien dat de optelling "+" een afbeelding is van X op . Hetzelfde geldt voor de operatoren "-", "x" en "/" en machtsverheffen en worteltrekken.
En we hebben inmiddels meer operatoren voorbij zien komen, zoals en in de propositielogica. Een ander voorbeeld is de doorsnede ∩ tussen twee verzamelingen .
De operatoren "+", "-", "x" en "/" zijn net als ∩ en X tweeplaatsige operatoren. Het complement Ac en de ontkenning zijn eenplaatsige operatoren.
Definitie:
Een operatie R is een afbeelding van A X B in C en we noteren deze als aRb waarbij a en b elementen van A respectievelijk B zijn.
Vaak zullen A en B identieke verzamelingen zijn, zoals in bovenstaande voorbeelden, maar dit is niet noodzakelijk.
Generalisatie
We kunnen een operator definiëren van A1 X ... X An naar B. We spreken dan van een n-plaatsige operator.
Equivalentie relaties
[bewerken]Een equivalentierelatie is een relatie die elementen met een gemeenschappelijk kenmerk aan elkaar koppelt.
Voorbeeld: bij de meetkundige figuren kunnen we een equivalentierelatie definieren "heeft n hoeken". Dan zijn de volgende figuren equivalent:
![]()
Afb. 5.4
Definitie
Een equivalentierelatie R op een verzameling X is een tweeplaatsige relatie ab op X met de eigenschappen:
- reflexiviteit: voor alle x X geldt: xx (elke x is equivalent met zichzelf)
- symmetrie: voor alle x,yX geldt: als xy, dan yx (als x equivalent is met y, dan is y dit ook met x)
- transitiviteit: voor alle x,y,zX geldt: als xy en yz, dan xz
Een equivalentie relatie R op een verzameling V is dus een deelverzameling van V X V.
Notatie:
Er zijn verschillende notaties in gebruik. Zowel de hierboven genoemde ab als ab en ab worden gebruikt. Om de relatie R expliciet aan te geven, kunnen we aRb gebruiken. Het niet equivalent zijn van a en b kunnen we aangeven met a≁b of ab.
Voorbeelden van equivalentie relaties:
- De kleur van de schoenen van leerlingen op een school
- Musici die op dezelfde datum geboren zijn
- De restwaarde van natuurlijke getallen bij delen door n.
- Functies f(x)=ax+b met f(2)=3
- De waarden x die dezelfde waarde f(x)=sin(x) hebben
- Congruente driehoeken
- Gelijkvormige driehoeken
De waarden van een equivalentie relaties groeperen de elementen van een verzameling in een aantal equivalentierelaties. Dus als xy, dan zitten x en y in dezelfde equivalentieklasse. We noteren de quivalentieklasse van x met .
Omdat een equivalentierelatie reflexief is, zit elk element van een verzameling in een van de equivalentieklassen. Equivalentieklassen zijn onderling disjunct (niet overlappend), want als y in twee equivalentieklassen en zou zitten, zou xy en yz, wat volgens de transitiviteit betekent xz, dus = . De equivalentieklassen vormen samen dus een partitie (zie hoofdstuk 2) van de verzameling waarop de equivalentierelatie gedefinieerd is.
(Partiele) ordening
[bewerken]Ordenen is een heel elementaire activiteit van het menselijk brein. De eerste ordening die we als kind leren is vaak van klein naar groot, bijvoorbeeld houten blokjes van klein naar groot leggen. Of dominostenen van 0 naar 6 leggen. We leren dat 2 minder is dan 3, en iemand die 2 koekjes heeft, heeft er minder dan iemand die 5 koekjes heeft. OOk in de wiskunde komen we verschillende ordeningen tegen.
In het eerste hoofdstuk benadrukten we dat een verzameling geen ordening bezat. Dus de verzameling {1,2} is hetzelfde als de verzameling {2,1}. Daarmee bedoelden we dat een verzameling geen ordening in zichzelf bezit. We kunnen wel een ordening op een verzameling definiëren. Die is dan geen deel van de verzameling, maar daar bovenop gedefinieerd. Is dat nuttig? Ja, want soms zijn er verschillende ordeningen mogelijk op 1 zelfde verzameling.
Voorbeelden van ordeningen:
- Een verzameling letters of woorden kunnen we alfabetisch ordenen.
- Een verzameling meetkundige figuren kan geordend worden door naar de oppervlakte te kijken, of naar het aantal hoeken.
- Laat A={0, 1, 2, 3}. Hierop definiëren we de standaard ordening van de natuurlijke getallen, 0<1<2,3.
Een tweede ordening die we hierop kunnen definiëren is 0<1, 0<2, 1<3, 2<3.
- Neem de natuurlijke getallen. Hierop kunnen we de standaard ordening 0<1<2,3<4 etc definieren, maar we zouden die ook kunnen ordenen door eerste de oneven getallen en dan de even getallen te nemen, als volgt:{1 < 3 < 5 < 5 < 7 < ..., 0 < 2 < 4 < 6 ... te ordenen.
Definitie
Ordeningen zijn een vorm van binaire relaties. Laat V een verzameling zijn en R een relatie op V, d.w.z. een relatie op de elementen van V X V. We noemen R een ordening als de relatie reflectief, antisymmetrisch en transitief is.
- Voor alle a V geldt aRa (reflectief).
- als aRb en bRa dan a = b (antisymmetrisch of asymmetrisch)
- als aRb en bRc dan aRc (transitief).
Deze definitie lijkt dus sterk op die van equivalentieklasse, en het verschil is dat deze relatie a-symmetrisch in plaats van symmetrisch is.
Definitie
We noemen een ordening een partiele ordening als niet tussen alle elementen een < of ≤ bestaat. Met andere woorden: niet alle elementen zijn vergelijkbaar.
Een ordening waarbij wel alle elementen van een verzameling vergelijkbaar zijn, noemen we een totale orde.
Binnen de partiele ordeningen worden nog 2 vormen onderscheiden: strikt en niet strikt.
Definitie
Een ordening P=(V,<) noemen we een strikte partiele ordening wanneer voor alle vergelijkbare paren (a,b) van V X V geldt:
- a < b of b < a (antisymmetrisch of asymmetrisch)
- als a < b en b < c dan a < c (transitief).
Kortom, de reflectiviteit geldt dan niet. Een strikte ordening wordt ook wel een sterke of niet-reflexieve ordening genoemd, een niet strikte ordening wordt ook wel zwak of reflexief genoemd.
Als voor elk tweetal elementen a en b van V geldt dat ze vergelijkbaar zijn, dus a ≤ b of b ≤ a, dan noemen we de ordening totaal. Deze worden ook lineaire ordeningen of ketting ordeningen genoemd.
Voorbeelden van partiele ordeningen
Omdat je je misschien in eerste instantie niet zo veel kunt voorstellen bij een partiele ordening, geven we enkele voorbeelden:
- Blokfluiten zijn een deelverzameling van de verzameling blaasinstrumenten. Dat geldt ook voor trombones. Maar blokfluiten en trombones zijn geen deelverzameling van elkaar en hebben niet direct een onderlinge vergelijking.
- Neem de verzameling van de natuurlijke getallen . Orden deze op deelbaarheid. Daarmee bedoelen we 1<2, want 1 deelt 2. 1<3, want 1 deelt 3. 1<4 en 2<4, want zowel 1 als 2 delen 4. Dit is een voorbeeld van een partiele ordening, want bijvoorbeeld 2 en 3 zijn niet vergelijkbaar.
- Neem een verzameling A, laat P(A) de machtsverzameling van A zijn. Dan kunnen we een ordening op de deelverzamelingen van P(A) definiëren door A1 ≤ A2 dan en slechts dan als A1 ⊆ A1. We noemen dit een ordening op inclusie. Dit is een partiele ordening, want als we van {1, 2, 3} de deelverzamelingen {1,2} en {1,3} bekijken, zijn deze niet vergelijkbaar.
- Een ander voorbeeld van een partiele ordening door inclusie is lokatie. Bijvoorbeeld de Kalvermarkt en het Waterlooplein liggen in Amsterdam. Amsterdam ligt in Noord-Holland. Noord-Holland ligt in Nederland. Nederland ligt in Europa. Europa ligt op de Aarde. We noteren Kalvermarkt < Amsterdam, Waterlooplein < Amsterdam, Amsterdam < Noord-Holland, etc. Het Binnenhof ligt in Den Haag. Den Haag ligt in Zuid-Holland. Zuid-Holland ligt in Nederland.
Amsterdam is in deze ordening niet < of > dan Den Haag, ze zijn in deze ordening niet vergelijkbaar. Amsterdam is wel vergelijkbaar met de Kalvermarkt en met de provincie Noord-Holland. Kalvermarkt en Waterlooplein liggen allebei in Amsterdam, maar zijn onderling niet vergelijkbaar. - Kijk naar familierelaties. We kunnen "Is kind van" noteren als "<" .
In dit voorbeeld geeft de pijl "<" dan aan, en staat voor "is kind van". De transitiviteit geldt, al moeten we dan lezen "stamt af van". Niemand is kind van zichzelf, dus de ordening is strikt. Het is duidelijk dat er niet-vergelijkbare elementen zijn, zoals Jan en Abdul, en Mike en Achoura.
Extremen
- Als er een element m is waarvoor geldt dat m ≤ a voor alle a in de ordening, dan wordt m het kleinste element van de verzameling genoemd.
- Als er een element m is waarvoor geldt dat a ≤ m voor alle a in de ordening, dan wordt m het grootste element van de verzameling genoemd.
Merk op dat er voor elke ordening maar 1 grootste en 1 kleinste element in een verzameling kan zijn.
Bewijs: Stel dat er twee grootste elementen, m1 en m2 zijn.
Omdat m1 het grootste element is, is m2 ≤ m1.
Omdat m2 het grootste element is, is m1 ≤ m2. Dus m2 ≤ m1 en m1 ≤ m2. Volgens de 2e eigenschap bij de definitie van een ordening hierboven geldt dus m1 = m2.
Merk op dat niet elke verzameling een grootste of kleinste element heeft. Neem bijvoorbeeld A={x| X.0 en x<1}. Dat is dus de verzameling van alle breuken die > 0 en < 1 zijn. 0 zit daar zelf niet in, en voor elke breuk 1/n kunnen we een element 1/(n+1) bedenken dat nog kleiner is. Op dezelfde manier kunnen we voor elke breuk n/(n+1) een breuk (n+1)/(n+2) bedenken die nog dichter bij 1 ligt.
We noemen een element p van verzameling V maximaal als er geen element a bestaat zo dat a >p. Omgekeerd noemen we een element p minimaal als er geen element a bestaat zo dat a>p.
Notatie
Er zijn een aantal manieren gebruikelijk om (eindige) partiele ordeningen aan te geven. De minst overzichtelijke methode is het opsommen van paren zoals aa, ab, ac, ad, bd, etc. Het werkt al een stuk overzichtelijker wanneer we de paren in een matrix weergeven.

Afb. 5.7
Nog iets beter wordt het wanneer we het weergeven als Hasse diagram:

Afb. 5.8
Een laatste mogelijkheid biedt een weergave in de vorm van bolletjes:

Afb. 5.9
Deze vorm wordt ook wel een vergelijkbaarheidsgraaf genoemd.
Een Hassediagram heeft een paar regels:
- de kleine elementen staan onderaan, en dan oplopend naar boven.
- pijlen zijn dus niet nodig.
- er worden alleen relaties aangegeven tussen elementen en de elementen die 1 stap groter zijn. Dus niet met zichzelf, en niet met elementen die weer boven heet eerst grotere element liggen.
In de 2e helft van de 20e eeuw is de theorie over ordeningen dermate gegroeid dat ze een aparte tak van de wiskunde is geworden, de w:Ordetheorie.
Ordeningen spelen een belangrijk rol in de universele algebra, in de topologie en in de categorie theorie.
Engels
[bewerken]- Afbeelding: mapping of gewoon map
- Equivalentierelatie: Equivalence relation
- Operatie: operator, operation
- Ordening: ordering
- Partiele ordening: partial ordening of afgekort poset (partially ordered set).
- Plaatsigheid: ary
- Relatie: relation
Opgaven
[bewerken]Opgaven Relaties
[bewerken]- V.1 Zijn de volgende beweringen Waar of niet waar?
- V.1.a Een relatie tussen elementen van verzameling V en verzameling W is een deelverzameling van het Cartesisch product V X W
- V.1.b Een relatie tussen elementen van een verzameling V raakt altijd alle elementen van die verzameling
- V.2: schets een derde relatie tussen A en B in het voorbeeld van relaties (fig 5.2).
Opgaven Afbeeldingen
[bewerken]- V.11 Zijn de volgende beweringen Waar of niet waar?
- V.11.a elke afbeelding van A in B is een relatie tussen A en B
- V.11.b elke relatie tussen 2 verzamelingen A en B is een functie van A naar B.
- V.11.c Afbeeldingen kunnen alleen op eindige verzamelingen gedefinieerd worden.
- V.11.d Het Domein van een afbeelding is altijd gelijk aan het codomein.
Opgaven Operaties
[bewerken]- V.21 Zijn de volgende beweringen Waar of niet waar?
- V.21.a Optellen is een operatie op de verzameling Natuurlijke getallen.
- V.21.b Vermenigvuldigen is een operatie op de verzameling Gehele getallen
- V.21.c Optellen is geen operatie op de verzameling rationele getallen
- V.21.d Een operatie is altijd gedefinieerd voor elk element van zijn domein.
- V.22 In de automatiseringen plakken programmeurs vaak teksten achter elkaar met een operatie die ze concatenatie noemen. Twee teksten (in de automatisering meestal "strings" genoemd) worden dan achter elkaar geplaatst. Als operatie symbool wordt meestal "&" gebruikt. "Plein" & " 2" levert dan "Plein 2". Geef aan wat "Abc " & "cbA" oplevert.
- V.23 Is deze concatenatie operatie associatief? Is deze operatie commutatief?
Opgaven Equivalentie klassen
[bewerken]- V.31 Zijn de volgende beweringen Waar of niet waar?
- V.31.a Binnen een equivalentieklasse is elke element equivalent met zichzelf.
- V.31.b Congruente driehoeken zijn een voorbeeld van een equivalentieklasse
- V.31.c Je kunt rode bloemen als equivalentieklasse definiëren.
- V.31.d is een element in een equivalentieklasse.
- V.32 Geef twee mogelijke equivalentieklasse indelingen van {a, b, c}
- V.33 Welke deelverzamelingen zijn mogelijke equivalentieklassen van {a, b}?
- V.34 De volgende relatie is gedefinieerd op {a, b, c}: {(a,a), (b,b), (a,c), (c,c)}. Welke equivalentieklassen horen hier bij?
Opgaven Ordeningen
[bewerken]- V.41.a Elke partiele ordening is een afbeelding.
- V.41.b Elke partiele of volledige ordening op verzameling A is een deelverzameling van A X A.
- V.41.c Een partiele ordening kan alleen op eindige verzamelingen worden gedefinieerd
- V.41.d Een verzameling met een partiele ordening kan een grootste element hebben, maar hoeft dat niet
- V.41.e Een eindige verzameling heeft altijd maar 1 grootste element.
- V.42: Laat zien dat voorbeeld 3, de partiele ordening van plaatsen en gebieden, een ordeningsrelatie is.
- V.43: Laat zien dat de partiele ordening van P(A) door inclusie een partiele ordening is.
- V.44: Teken een Hassediagram van alle elementen waarbij de ordeningsrelatie a|b (a deelt b) is voor de getallen 1 t/m 9.
Samenvatting: In dit hoofdstuk heb je geleerd dat:
- Wat een afbeelding is
- Wat een equivalentieklasse is
- wat een operator is
- wat een partiele ordening is
- en je hebt gezien hoe functies gebaseerd zijn op de theorie van verzamelingen.
VI Booleaanse logica
[bewerken]Na het bestuderen van dit hoofdstuk:
- Weet je wat er met booleaanse logica en booleaanse algebra bedoeld wordt.
- Kun je de operatoren EN, OF en NIET gebruiken
Operatoren
[bewerken]In hoofdstuk 1 zagen we een verzameling voorbij komen met twee elementen, L={Waar, Onwaar}.
Hierop definiëren we een aantal operatoren, en , en .
De is EN, terwijl de OF operator is. We bekijken ze een voor een.
In dit boek gebruiken we W=Waar en O=Onwaar. maar in veel boeken wordt de Engelse T=True en F=False gebruikt. Dat zien we soms ook in Nederlandstalige boeken. We kunnen ook Waar als 1 en Onwaar als 0 noteren.
De EN operator
In de Nederlandse taal gebruiken we het woord EN in zinnen als 'Jan zit op zijn kamer EN Marie is op de manage'. Die zin is alleen waar als beide onderdelen waar zijn, dus als het waar is dat Jan op zijn kamer zit en als Marie op de manage is.
Noem de eerste zin p en de tweede zin q. Er zijn dan 4 mogelijkheden:
| p | q | pq |
|---|---|---|
| W | W | W |
| W | O | O |
| O | W | O |
| O | O | O |
Hierbij staat W telkens voor waar en O voor Onwaar.
Zodra een van de twee beweringen Onwaar is, is de samenstelling ook Onwaar.
De EN wordt ook wel inclusie genoemd.
De OF operator
Het woordje OF geven we in de booleaanse logica een wat striktere betekenis dan in het gewone taalgebruik, maar de betekenis komt toch goed overeen.
Wanneer we zeggen "Jan is naar de supermarkt of naar de drogist", dan is dat een combinatie van 2 beweringen, namelijk "Jan is naar de supermarkt" of "Jan is naar de drogist".
Ook dit kunnen we in een tabelletje onderbrengen. Noem de eerste bewerking weer p en de 2e bewering q. Er zijn weer 4 mogelijkheden:
| p | q | pq |
|---|---|---|
| W | W | W |
| W | O | W |
| O | W | W |
| O | O | O |
Dus de samenstelling pq is waar dan en alleen dan als een van de twee beweringen waar is.
De OF wordt ook wel disjunctie genoemd.
NIET
Ten slotte is er nog de negatie NIET.
| p | p |
|---|---|
| W | O |
| O | W |
Dit waren de 3 basis operatoren. Hiermee kunnen we een aantal andere operatoren definiëren.
De XOR operator
De OF heeft in het gewone spraakgebruik een dubbele betekenis. De eerste betekenis hebben we hierboven gezien. Maar soms willen we dat mensen echt een keuze maken, zoals in "wil je thee of koffie?". Als we alleen de bovenstaande OF zouden hebben, zou iemand op de vraag "Wil je thee of koffie?" kunnen antwoorden met "ja, graag" als hij een van de twee wil drinken. Als we echt willen dat één van de twee ja is, kunnen we kiezen voor de Exclusieve disjunctie, oftwel de XOR, de exlusive OR.
| p | q | pq |
|---|---|---|
| W | W | O |
| W | O | W |
| O | W | W |
| O | O | O |
De Exclusieve OR wordt minder vaak gebruikt dan de gewone OF.
De Logische implicatie
De logische implicatie komt neer op 'uit p volgt q'.
Notatie: p → q of p ==> q of pq
We kunnen p → q uitschrijven als waarheidstabel:
| p | q | p → q |
|---|---|---|
| W | W | W |
| W | O | O |
| O | W | W |
| O | O | W |
We krijgen dezelfde waarheidstabel wanneer we definiëren:
. We kunnen daarom de logische implicatie p q uitschrijven als p
Deze tabel verdient nog wel wat toelichting. Zoals je ziet is waar als p onwaar is, onafhankelijk van q. Dat is een keuze. Maar het verschilt wel met wat we soms uit het gewone spraakgebruik ons voorstellen. Als iemand zegt: Als het morgen warm is, trakteer ik op ijs, bedoelt die persoon daarmee meestal 'als het niet warm is, trakteer ik niet op ijs.' Maar wanneer we 'het is morgen warm' p noemen, en 'ik trakteer op ijs' q noemen, dan krijgen we de volgende waarheidstabel:
| het is morgen warm | ik trakteer op ijs | als het morgen warm is, trakteer ik op ijs |
|---|---|---|
| W | W | W |
| W | O | O |
| O | W | W |
| O | O | W |
Dan zien we dat als het morgen niet warm is, de persoon zijn belofte in elk geval niet gebroken heeft, of hij nu op ijs trakteert of niet. Het is daarom niet onlogisch om deze definitie te hanteren.
Equivalentie:
betekent: .
De laatste operator die hier behandelen is de equivalentie. Deze spreken we vaak uit als "dan en slechts dan", waarmee we bedoelen "dan, en alleen dan".
Notatie:: is gebruikelijk maar ook wordt gebruikt.
Gebruik van de operatoren
[bewerken]We kunnen met deze operatoren rekenen. Dit wordt ook wel Booleaanse algebra genoemd. Net als bij gewoon rekenen kunnen we haakjes gebruiken om de voorrang aan te geven. Normaal gaat voor . We geven hier een paar voorbeelden:
- WO = WW=W
- WO O = O O = O
- WO O) = W O = O
Booleaanse algebra
[bewerken]Zoals hierboven getoond kunnen we met de operatoren , en 'rekenen'.
Ze hebben een aantal eigenschappen die we ook bij de gewone getallen tegenkomen: associativiteit
- (eigenschap 6.1)
- (eigenschap 6.2)
commutativiteit
- (eigenschap 6.3)
- (eigenschap 6.4)
distributiviteit
- (eigenschap 6.5)
- (eigenschap 6.6)
Ontkenning
- (eigenschap 6.7)
- (eigenschap 6.8)
En ja, deze eigenschappen kwamen we ook tegen bij de deelverzamelingen waar we werkten met de operatoren ∪, ∩ en Complement.
Identiteitselement
Er is nog een overeenkomst: zowel als hebben een identiteitselement.
Laat W=Waar en O=Onwaar. Dan geldt
- pWaar= p voor alle proposities (beweringen) p
- pOnwaar = p voor alle proposities p.
Notatie
[bewerken]Het is gebruikelijk om voor beweringen de hoofdletters P en Q te gebruiken. In dit wikibook gebruiken we de kleine letters p en q, en reserveren de hoofdletters P en Q voor de verzamelingen van alle logische beweringen.
Gebruik
[bewerken]- Booleaanse algebra wordt o.a. gebruikt in de elektronica. Hier zijn speciale symbolen voor de AND, OR en NOT schakelingen:
- In de Informatica worden waarheidsschema's en booleaanse algebra op grote schaal gebruikt bij het programmeren en bij het bevragen van databases zoals met SQL.
Een gefingeerd voorbeeld:
SELECT "Operationeel", salarisschaal, COUNT(distinct Medw_no), SUM(sal_bruto)
FROM Medewerker, Salaris, Medewerker_groep
WHERE medewerker.salarisschaal = Salaris.salarisschaal
AND medewerker.groepnr = Medewerker_groep.groepnr
AND NOT (Medewerker.groep = "Manager" OR Medewerker.groep = "Secretaris/Secretaresse")
GROUP BY salarisschaal
UNION
SELECT "Management", salarisschaal, COUNT(distinct Medw_no), SUM(sal_bruto)
FROM Medewerker, Salaris, Medewerker_groep
WHERE medewerker.salarisschaal = Salaris.salarisschaal
AND medewerker.groepnr = Medewerker_groep.groepnr
AND (Medewerker.groep = "Manager" OR Medewerker.groep = "Secretaris/Secretaresse")
GROUP BY salarisschaal
In bovenstaand voorbeeld wordt zowel de AND, de OR als de NOR operator gebruikt. Tevens wordt de UNION, oftewel de Vereniging gebruikt.
Meerwaardige logica
[bewerken]De Booleaanse algebra en de standaard propositielogica zijn tweewaardig. Er zijn ook meerwaardige logica's gedefinieerd. Vaak is daarbij sprake van een waarschijnlijkheidsfunctie. Meerwaardige logica worden in het Engels ook wel Fuzzy Logic geneomd.
Een voorbeeld van een 3-waardige logica zou zijn (True, False, Unknown}. We gebruiken in deze paragraaf even de Engelse True en False, omdat we met Waar, Onwaar en Onbekend geen unieke 1-letterige afkortingen hebben. We kunnen dan de EN definieren als:
| p | q | pq |
|---|---|---|
| T | T | T |
| T | F | F |
| W | U | U |
| F | T | F |
| F | F | F |
| F | U | U |
Een verdere uitwerking valt buiten de scope van dit boek.
Engels
[bewerken]- Onwaar: False
- Waar: True
Opgaven
[bewerken](@@@ nog uit te breiden)
Samenvatting: In dit hoofdstuk heb je geleerd dat:
- wat de logische operatoren zijn
- hoe je er mee kunt rekenen
VII Wetten van de Morgan
[bewerken]Na het bestuderen van dit hoofdstuk:
- Weet je wat de wetten van de Morgan voor verzamelingen zijn
- Kun je deze twee wetten gebruiken
August de Morgan was een wiskundige en logicus die leefde van 1806 tot 1871.
Wetten van de Morgan voor logische beweringen
[bewerken]In de inleiding noemden we al dat er een stevig verband ligt tussen de logica en de leer van de verzamelingen. In het vorige hoofdstuk gaven we een introductie in de booleaanse en propositie logica.
De wetten van de Morgan voor de propositielogica zijn:
en
Bewijs
[bewerken]Voor het bewijs maken we gebruik van waarheidstabellen: we schrijven de verschillende combinaties van de waarden van p en q uit:
p q pq W W W O W O W O O W W O O O O W
Als P waar is, en q waar is, dan is pq Waar, dus is Onwaar. Etc.
Hiermee hebben we de linkerhelft van de eerste wet van Morgan uitgewerkt. Dan blijft de rechter helft over:
p q p q W W O O O W O O W O O W W O O O O W W W
Bij elke zelfde combinatie van de waarden van p en q krijgen we voor en dezelfde waarde, de uitdrukkingen zijn dus identiek.
Het bewijs van de tweede stelling is een van de opgaven.
Wetten van de Morgan voor verzamelingen
[bewerken]Laten A, B en C willekeurige verzamelingen zijn. Dan zijn de twee wetten van de Morgan voor verzamelingen:
- (A ∩ B)c=Ac ∪ Bc
- (A ∪ B)c=Ac ∩ Bc
Bewijs
[bewerken]Bekijk de iets krachtiger beweringen:
- C - (A∪B) = (C-A)∩(C-B)
- C - (A∩B) = (C-A)∪(C-B)
Deze zijn iets krachtiger, want door C=U=de universele verzameling te kiezen, hebben we de wetten van de Morgan.
We beginnen met:
- C - (A∪B) = (C-A)∩(C-B)
Laat aC - (A∪B). Volgens de definitie van de verzameling X-Y geldt dan dus dat aC en aA∪B. Dat laatste betekent dat aA en dat aB. Kortom (aC en aA) en (aC en aB), oftewel aC-A en aC-B. ==> C - (A∪B) ⊆ (C-A)∩(C-B).(resultaat (i))
Dan moeten we nog de andere kant uit bewijzen:
Laat a(C-A)∩(C-B). ==> aC-A en aC-B.
aC-A ==> aC en aA
aC-B ==> aC en aB
Uit aA en aB ==> aA∪B
==> aA en aA∪B ==> a C - (A∪B) ==> (C-A)∩(C-B) ⊆ C - (A∪B) (resultaat (ii))
We kunnen resultaat (i) en resultaat(ii) combineren tot C - (A∪B) = (C-A)∩(C-B).
Dan moeten we natuurlijk nog de tweede wet bewijzen. Ook deze doen we in twee stappen, eerste bewijzen we dat de linkerhelft een deelverzameling is van de rechterkant, en vervolgens bewijzen we dat de rechterkant een deelverzameling is van de linkerkant:
- C - (A∩B) = (C-A)∪(C-B)
Laat a(C - (A∩B)) ==>
aC a(A∩B) ==>
aC (aA aB) ==>
(Noem aA even p en noem aB even q. Dan kunnen we (p q) volgens de 2e wet van Morgan voor logica herschrijven als p q)
aC ( a A a B) ==>
aC ( a A a B) (gebruik eigenschap 6.3) ==>
(a(C-A) (a(C-B)).
Oftewel C - (A∩B) ⊆ (C-A)∪(C-B)
Dan hebben we nog de andere kant uit te bewijzen, dus (C-A)∪(C-B) ⊆ C - (A∩B). Dit bewijs geven we als opgave.
Engels
[bewerken](geen)
Opgaven
[bewerken]- VII.1 Toon aan dat .
- VII.2 Toon aan dat (C-A)∪(C-B) ⊆ C - (A∩B)
Samenvatting: In dit hoofdstuk heb je geleerd wat de wetten van de Morgan zijn.














































![{\displaystyle [x],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57d39d8cf0d128792d2e0ca013101a731a888ae5)
![{\displaystyle [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07548563c21e128890501e14eb7c80ee2d6fda4d)
![{\displaystyle [z]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19b38ec99854bf1fd78d52db38a1518ffed72394)




























