Sterkteleer/Basisbegrippen-2
Wet van Hooke voor isotrope materialen
[bewerken]Algemeen
[bewerken]Bij de bespreking van de evenwichtsvergelijkingen in functie van de spanning werd erop gewezen dat voor de oplossing van deze vergelijkingen meestal de vervormingen in rekening gebracht moeten worden. Er waren 6 onbekende spanningscomponenten en slechts 3 evenwichtsvergelijkingen.
Uit de bespreking van de ruimtelijke vervormingstoestand, blijkt dat de verplaatsingen en vervormingen beschreven worden door negen veranderlijken, namelijk de drie verplaatsingskomponten u, v en w en de zes vervormingscomponenten εx, εy, εz, γxy, γyz en γzx. Tussen deze 9 veranderlijken werden de zes geometrische betrekkingen opgesteld.
Het totaal aantal onbekenden bedraagt 15, waartussen we slechts 9 vergelijkingen hebben opgesteld, waardoor het stelsel vergelijkingen onbepaald zal zijn.
Om de onbepaaldheid van het stelsel op te heffen, worden zes verbanden opgesteld tussen de spanningen en de vervormingen. Deze verbanden zijn verschillend voor elk materiaal. De Britse wetenschapper Robert Hooke was in 1678 de eerste die een wiskundige formulering opstelde voor het spannings-vervormingsgedrag van een materiaal. Deze verbanden tussen spanning en vervormingen worden daarom ook wetten van Hooke of materiaalwetten genoemd.
De algemene afleiding van deze materiaalwetten, gebaseerd op principes uit de toegepaste materiaalkunde en de thermodynamica, wordt in dit boek sterkteleer niet behandeld. In dit boek beperken we ons tot homogene, lineair elastische, isotrope materialen. Deze begrippen zullen in de volgende paragrafen worden toegelicht.
Het begrip Elasticiteit
[bewerken]Een vast lichaam is opgebouwd uit moleculen, waartussen intermoleculaire krachten werken. Deze intermoleculaire krachten verzetten zich tegen elke vervorming van het lichaam. Nochtans blijkt dat geen enkel fysisch lichaam volmaakt onvervormbaar is. Onder de inwerking van uitwendige krachten worden de moleculen verplaatst en deze verplaatsing gaat door tot er een nieuw evenwicht ontstaat tussen de uitwendige en inwendige krachten. Het lichaam bevindt zich in een vervormde toestand.
Bij deze vervorming zullen de uitwendige krachten arbeid leveren. Deze arbeid is een vorm van energie en de arbeidsenergie wordt, geheel of gedeeltelijk, getransformeerd naar potentiële energie van de vervormingen, of kortweg vervormingsenergie. De veer in een speelgoedautootje of in een horloge zijn voorbeelden van een opstapeling van potentiële energie in een vervormd lichaam. Als de krachten die de vervorming veroorzaakten geleidelijk aan verminderd worden, dan zal het lichaam geheel of gedeeltelijk terug zijn oorspronkelijke vorm aannemen. Als de vervorming aanzienlijk was, dan zal het lichaam over het algemeen niet volledig zijn oorspronkelijke vorm terugkrijgen.
De eigenschap van een lichaam om na vervorming terug zijn oorspronklijke vorm aan te nemen, noemt men elasticiteit. Een lichaam is volmaakt elastisch als het bij het wegnemen van de belasting volledig zijn initiële vorm aanneemt. In het andere geval spreekt men van gedeeltelijke elasticiteit. In dit laatste geval zal een deel van de arbeidsenergie die door de uitwendige krachten bij vervorming geleverd worden, gedissipeerd worden onder de vorm van warmte of een andere energievorm.
De constructiematerialen zoals de meeste metalen, steen, beton, hout en dergelijke, kunnen als volmaakt elastisch beschouwd worden binnen zekere grenzen van de spanningen. Wil men een duurzame constructie ontwerpen, dan is het meestal noodzakelijk om alle blijvende vervormingen te vermijden. Hiertoe dient een ontwerper de afmetingen van alle structuurelementen zodanig te bepalen, dat de vormveranderingen onder alle mogelijke optredende belastingen, volmaakt elastisch blijven. Een zekere mate van niet-elastische vervorming wordt meestal enkel toegestaan bij zware accidentele belastingen zoals bijvoorbeeld aardbevingen.
Elasticiteitsmodulus
[bewerken]
De afbeelding rechts stelt een eenvoudige trekproef voor, waarin een staaf onderworpen wordt aan een normaalkracht volgens de aslijn. Het stuk ab met lengte L wordt verlengd naar a'b' met lengte L+δ.
Uit een dergelijke trekproef blijkt dat voor vele materialen de totale verlenging δ van het deelstuk ab met lengte L, recht evenredig is met de aangelegde axiale trekkracht N=P en met de lengte L, en omgekeerd evenredig is met de dwarsdoorsnede A. Wiskundig uitgedrukt geeft dit:
| met | δ = totale verlenging (m) |
| P = externe trekkracht (N) | |
| L = oorspronkelijke lengte voor vervorming (m) | |
| A = oppervlakte van de sectie (m2) | |
| E = evenredigheidsfactor afhankelijk van het materiaal (N/m2). |
We zijn geïnteresseerd in hoe deze verlenging kan ontstaan. Veronderstellen we dat de staaf oneindig lang is. We beschouwen de dwarsdoorsnede m, die voor vervorming vlak is. Na het aanbrengen van de belasting verdeelt de snede m de staaf in twee delen die geometrisch identiek zijn en ook op een identieke wijze belast worden. Om symmetrieredenen zullen deze 2 gedeelten op dezelfde wijze vervormen, op een zodanige manier dat door het tegen elkaar plaatsen van de twee delen terug de oorspronkelijke staaf wordt verkregen, zonder scheuren. De enige mogelijke manier van vervorming is degene die voorgesteld op "figuur 3." in bovenstaande afbeelding, waarbij de dwarsdoorsnede vlak blijft en loodrecht op de aslijn. Dit is de zogenaamde wet van het behoud der platte vlakken van de dwarsdoorsnede, die voor het eerst werd geformuleerd door de Zwitser Johan Bernoulli in 1705.
Deze wet blijft geldig bij stukken met eindige lengte, behalve in de buurt van het aangrijpingspunt van de uitwendigekrachten, waar een ingewikkelde spanningstoestand heerst. In de middenzone ondergaan alle vezels dus een zelfde verlenging, die beschreven wordt door de relatieve lengteverandering of de rek ε (verlenging per lengteëenheid):
Aangezien alle vezels dezelfde rek ondergaan, zullen de spanningen gelijkmatig verdeeld zijn over de doorsnede A. Uit het evenwicht van 1 deelstuk van de staaf volgt dan de normaalspanning:
Door substitutie van deze laatste uitdrukkingen voor de rek en de spanning in de uitdrukking voor δ vinden we:
De factor E, die het verband legt tussen de normaalspanning σ en de rek ε, bij een zuiver centrische belasting van een lange staaf, noemen we de Elasticiteitsmodulus. De elasticiteitsmodulus E (en enkele andere materiaaleigenschappen) van enkele veel gebruikte materialen is gegeven in onderstaande tabel:
| Materiaalconstanten van enkele contructiematerialen | |||
|---|---|---|---|
| Materiaal | Elasticiteitsmodulus E [N/mm2] |
Poisson-coëfficient ν [ ] |
Uitzettingscoëfficient α [1/K] |
| staal | 210.000 | 0,28 - 0,30 | 12,0 x 10-6 |
| gietijzer | 100.000 | 0,25 - 0,27 | 11,4 x 10-6 |
| koper | 110.000 | 0,33 | 16,8 x 10-6 |
| aluminum | 70.000 | 0,30 | 25,5 x 10-6 |
| lood | 16.000 | 0,43 | 29,4 x 10-6 |
| beton | 25.000 - 40.000 | 0,17 | 12 x 10-6 |
| baksteen | 10.500 | 0,1 - 0,2 | 5 x 10-6 |
| glas | 66.000 | 0,25 - 0,33 | 8,9 x 10-6 |
| hout (langsrichting) | 10.000 | 3 x 10-6 - 9 x 10-6 | |
De waarden van de elasticiteitsmodulus, zoals opgenomen in bovenstaande tabel, zijn gemiddelde waarden. Afhankelijk van de productiewijze of de specifieke samenstelling van de materialen, kunnen deze waarden lichtjes variëren.
In de formule is E onafhankelijk van de grootte van de rek of de spanningen. De rekken zijn dus proportioneel met de spanningen. Dergelijke materialen noemt men lineair elastisch. Alle verdere berekeningen in dit boek sterkteleer zullen uitgewerkt worden in de veronderstelling dat de materialen lineair elastisch zijn. De hierboven genoemde materialen kunnen allen als lineair elastisch beschouwd worden, zolang de spanning onder een materiaalafhankelijke bovengrens blijft, vloeigrens genaamd. Voor elk materiaal afzonderlijk moet (desnoods proefondervindelijk) onderzocht worden tot welke waarde van de spanningen een materiaal zich lineair elastisch gedraagt. Dergelijk onderzoek valt buiten het opzet van dit boek sterkteleer en hoort thuis in de Materiaalkunde of Toegeapste Materiaalkunde.
Superpositiebeginsel
[bewerken]We beschouwen een staaf waarop meerdere krachten gelijktijdig inwerken, zoals op de figuur hieronder:
We kunnen de totale verlenging δ van deze staaf bereken met de formule uit de trekproef:
Een beetje rekenwerk levert volgende formule op:
Het blijkt dat de verlenging δ een lineaire functie is van de uitwendige krachten. De eerste term is de de verlenging als alleen de kracht P1 inwerkt. De tweede en term geeft de verlenging onder invloed van enkel P2, en de derde deze onder invloed van P3. De totale verlenging is de som van de verlenging mochten deze krachten alleen inwerken.
In alle gevallen van samengestelde belastingen, waar de verplaatsingen lineaire functies van de uitwendinge belastingen, geldt dezelfde conclusie: De totale verplaatsing van elk punt wordt verkregen door de sommatie van de verplaatsingen van dit punt onder de afzonderlijke belastingen. Deze eigenschap noemt men het superpositiebeginsel. Het is geldig bij lineair elastische materialen en kleine verplaatsingen. Kleine verplaatsingen dient begrepen te worden als verplaatsingen die de interne krachtswerking niet (of quasi-niet) veranderen. Het superpositiebeginsel laat toe om problemen met ingewikkelde uitwendige krachtswerking om te zetten in een som van eenvoudigere deelproblemen.
Een voorbeeld waarbij de krachtswerking wel beïnvloedt wordt door de verplaatsing is getoond in onderstaande figuur:
Dit vakwerk bestaat uit twee staven AC en CB, gelegen in elkaars verlengde. Onder invloed van de vertikale last P zullen de staven uitgerekt worden, en ondergaat het punt C een verplaatsing δ naar C'. De staven roteren onder een hoek α. In de staven werken de inwendige staafkrachten S als gevolg van de externe kracht P. Wegens de symmetrie van het probleem gaan we ervan uit dat de staafkracht in beide staven gelijk is.
Het vertikaal krachtevenwicht in punt C' geeft:
In de driehoek ACC' geldt dat:
We kunnen, door elimininatie van sinα, S schrijven als:
Voor de relatieve verlenging van de staaf AC geldt (formules trekproef):
In de driehoek ACC' geldt voor de relatieve verlenging van de staaf AC eveneens hetvolgende:
Deze laatste formule kunnen we herwerken tot:
Gelijkstelling van de twee formules voor ε levert:
Enig rekenwerk levert:
Hoewel het materiaal van de staven voldoet aan de Wet van Hooke, neemt de verplaatsing δ niet lineair toe met de kracht. Het superpositiebeginsel is hier dus niet van toepassing. De krachtswerking kan hier slechts bepaald worden door de vervormingen in beschouwing te nemen. Dergelijke constructies noemt men statisch onbepaald of hyperstatisch. Op hyperstatische constructies wordt later in dit boek verder ingegaan.
Dwarscontractie
[bewerken]Bij een trekproef, zoals uiteengezet bij de elasticiteitsmodulus , stelt men vast dat de axiale verlenging (of verkorting in geval van druk) steeds gepaard gaat met een dwarse inkrimping (of uitzetting in geval van druk), zoals op de linkse figuur hieronder.
Deze inkrimping (of uitzetting) in de elastische zone, is zodanig dat de "verhouding " tussen de relatieve dwarse inkrimping en de relatieve axiale verlenging een constante is voor een gegeven materiaal.
Deze dimensieloze materiaalconstante "" wordt de poisson-coëfficiënt genoemd (zie ook Poisson-coëfficiënt op wikipedia). In dwarszin treed dus een rek op, ook al zijn er geen dwarse normaalspanningen. Deze dwarse rek heeft volgende grootte:
Dit betekent ook dat, indien in een punt een driedimensionale spanningstoestand heerst (zie rechtse bovenstaande figuur, waar de normaalspanningen getekend zijn) de rek in de x-richting tegengewerkt wordt door de spanningen in de y-richting en z-richting. Voor de drie richtingen kan dit, met behulp van het superpositiebeginsel, als volgt in formules worden uitgeschreven:
Uit deze vergelijkingen kan men een belangrijke eigenschap van de poisson-coëfficiënt afleiden. Beschouwen we de rechtse bovenstaande figuur het kubisch elementje dx dy dz en stel dat op alle vlakken een constante trekspanning σ=σx=σy=σz heerst. Onder deze alzijdige trekspanning zal een het lichaam dx dy dz een volumeverandering ondergaan, die we kunnen uitschrijven met de formule voor de kubische volumeverandering :
De rekken kunnen we uitschrijven in functie van de spanningen met de bovenstaande formules:
Dit geeft voor de kubische volumeverandering bij constante alzijdige trek:
Fysisch is het onmogelijk dat een lichaam dat aan een alzijdige trek onderworpen is, een volumevermindering zou ondergaan. De term moet daarom positief of nul zijn, waaruit volgt:
De waarde van de poisson-coëfficiënt voor enkele veel voorkomende constructiematerialen is opgegeven in de tabel in de paragraaf over de elasticiteitsmodulus.
Zuivere afschuiving - Glijdingsmodulus
[bewerken]Op de onderstaande linkse figuur werken op een vlak vierkant element de trekspanning σx en een de drukspanning σy = -σx.
In dit vlak bekijken we het vierkant ABCD, waarvan de zijden onder een hoek van 45° op de coördinaatassen staan. Op de zijnvlakjes van dit vierkant werkt een normaalspanning σ en een schuifspanning τ, zoals te zien in de middelste figuur (driehoek OBC).
In de driehoek OCB kunnen we het krachtenevenwicht uitschrijven, waarbij de notatie XY staat voor de oppervlakte tussen X en Y:
- er geldt:
- horizontaal evenwicht:
- vertikaal evenwicht:
- uitwerking levert:
De zijvlakjes van van het element ABCD worden dus uitsluitend belast door schuifspanningen. Men noemt deze spanningstoestand een toestand van zuivere afschuiving.
We gaan na hoe het vlakje ABCD vervormd. Omdat op de zijvlakjes geen normaalspanningen werken zullen de rekken ε gelijk zijn aan nul, volgens de formules afgeleid bij in de paragraaf over Dwarscontractie. Dit betekent dat de lengtes van de zijden AB, BC, CD en DA niet verandert. De diagonaal AC zal echter verlengen en de diagonaal BD verkorten, zodant het vierkant ABCD zal veranderen in een ruit A'B'C'D'. De hoek in A, die oorspronkelijk recht was, wordt nu kleiner met een hoeveelheid γ en wordt gelijk aan π/2-γ (zie de paragraaf over Glijding). De hoek in B wordt groter en zal na vervorming π/2+γ bedragen. γ is de eerder besproken glijdingshoek.
Een duidelijk beeld hiervan krijgen we door de vervormde zijde A'D' te laten samenvallen met de zijde AD (de lengtes blijven gelijk), en de figuur 45° te draaien (zie bovenstaande figuur rechts). Na de vervorming door de schuifspanningen krijgen we de figuur in de streeplijn. De hoek γ is quasi gelijk aan de glijding BB' gedeelde door de lengte van de zijde :
Als het materiaal lineair elastisch is, neemt de glijding lineair toe met de schuifspanning:
De evenredigheidsfactor G is een materiaalconstante en wordt glijdingsmodulus genoemd. Deze glijdingsmodulus is echter geen nieuwe materiaalconstante, omdat er een verband bestaat tussen de glijdingsmodulus G, de elasticiteitsmodulus E en de poisson-coëfficiënt ν . Dit verband kunnen we afleiden uit bovenstaande figuur.
De verlengde zijde OC' en de verkorte zijde OB' kunnen uitgeschreven worden in functie van de rekken:
In de driehoek OC'B' geldt:
Met inrekening van τ = σx = -σy kunnen we de rekken uitwerken (zie formules voor de rek in de paragraaf over Dwarscontractie ) :
Met behulp van de goniometrische hoekverschil-identiteit kunnen we de tangens ook uitwerken tot:
Voor zeer kleine hoeken geldt dat de tangens van een hoek (in radialen) quasi gelijk is aan die hoek zodat:
Gelijkstellen van de twee uitdrukkingen levert:
We kunnen dus concluderen dat de glijdingsmodulus G gelijk is aan:
Algemene elasticiteitswetten van Hooke voor isotrope materialen
[bewerken]Bij alle vorige afleidingen werd verondersteld dat E, ν en G materiaalconstanten zijn, welke in elk punt van dat materiaal onafhankelijk zijn van de richting. Dergelijke materialen noemt men isotroop. Niet alle materialen zijn isotroop: een duidelijk voorbeeld hiervan is bijvoorbeeld hout dat in de richting van de houtvezels een totaal verschillende stijfheid vertoont dan in de richting dwars op de houtvezels. Andere voorbeelden zijn gelaagde of vezelversterkte kunststoffen. Dergelijke niet-isotrope materialen worden bestudeerd in de elasticiteitsleer en worden in dit boek niet behandeld.
Voor isotrope materialen gelden dus de volgende elasticiteitswetten:
| Algemene elasticiteistwetten van Hooke voor isotrope materialen |
|---|
|
Indien in elk materiaalpunt de constanten E, ν en G dezelfde waarde hebben, noemt men het materiaal homogeen.
Verschil tussen Sterkteleer en Elasticiteitsleer
[bewerken]In de voorgaande paragrafen werden opeenvolgend volgende verbanden opgesteld:
- De evenwichtsvergelijkingen in functie van spanningen (link)
- De geometrische betrekkingen tussen verplaatsingen en vervormingen (link)
- De materiaalwetten van Hooke die het verband uitdrukken tussen spanningen en vervormingen (link)
Samen vormen deze vergelijkingen een stelsel van 15 differentiaalvergelijkingen in 15 onbekenden:
- De spanningen σx, σy, σz, τxy, τyz, τzx ;
- De vervormingen εx, εy, εz, γxy, γyz, γzx ;
- De verplaatsingen u, v, w.
In de elasticiteitsleer zal men trachten een exacte oplossing te vinden voor de 15 onbekenden in dit stelsel van 15 differentiaalvergelijkingen. Dit leidt meestal tot ingewikkelde en zeer omvangrijke wiskundige uitwerkingen. Tenzij voor zeer simpele gevallen zullen de wiskundige uitwerkingen te omslachtig en tijdrovend zijn om manueel uit te rekenen.
In de sterkteleer daarentegen vertrekt men meestal van een vereenvoudigde aanname voor de verplaatsingen u, v en w; waaruit dan verder op exacte wijze de vervormingen en de spanningen afgeleid worden. Dit heeft als gevolg dat de methodes van de sterkteleer enkel toepasbaar zijn voor structuren waar het vervormingsgedrag tamelijk doorzichtig blijft. Deze gevallen zullen in dit boek verder bestudeerd worden. Er wordt hierbij getracht om steeds te wijzen op de aard van de benadering, en de invloed ervan op de nauwkeurigheid van de resultaten.
Elastische vervormingsenergie in functie van spanningen en rekken
[bewerken]Arbeid geleverd door de uitwendige krachten
[bewerken]Bij de bespreking van het begrip "elasticiteit" werd reeds vermeld dat de arbeid, die tijdens de vervorming wordt verricht door de uitwendige krachten, in het lichaam wordt opgestapeld als vervormingsenergie.
Beschouwen we een balk waarop 1 kracht P werkt, zoals op de figuur hieronder, waarbij het materiaal de wet van hooke volgt:
Aangezien de doorbuiging δ volgens de werklijn van de kracht P recht evenredig toeneemt met de grootte van de kracht P, zal bij stijgende kracht P de doorbuiging proportioneel toenemen volgens de rechte in het diagramma rechts. Beschouwen we P1 als een tussenkracht waarmee de doorbuiging δ1 overeenstemt. Een elementaire toename dP van de kracht veroorzaakt een een aangroeiing dδ van de doorbuiging. De aanwezige kracht P1 levert op dit moment een arbeid P1.dδ, voorgesteld door het gearceerde deel van de figuur rechts. In de eindtoestand (kracht P, doorbuiging δ) zal de toegenomen kracht P een arbeid geleverd hebben, gelijk aan de oppervlakte van de volledige driehoek. Wiskundig kunnen we dit als volgt uitschrijven, waarbij Au de arbeid van de uitwendige kracht voorstelt:
Indien er meerdere uitwendige lasten Pi tegelijk inwerken, hoort bij elk van deze krachten een doorbuiging δi volgens de werklijn van deze krachten, zoals op de figuur hieronder.
We laten de uitwendige krachten gradueel toenemen van 0 tot hun uiteindelijke waarde, zodat ze op elk ogenblik in evenwicht zijn met de inwendige spanningen in de structuur. De arbeid die geleverd wordt door de uitwendige krachten, wordt als potentiële energie (vervormingsenergie) opgestapeld in de structuur. De grootte van deze arbeid is volledig bepaald door de eindtoestand, en wordt niet beïnvloed door de volgorde waarin de krachten werden aangebracht. Als we alle krachten tegelijkertijd gradueel laten toenemen krijgen we voor elke kracht een diagramma zoals in het geval er maar één kracht inwerkt . De totale arbeid van de uitwendige krachten kan dan neergeschreven worden als volgt:
De uitwendige arbeid is de som van de halve producten van elke uitwendige kracht met haar overeenkomstige verplaatsing. De reactiekrachten, welk ook uitwendige krachten zijn, worden in de uitdrukking voor de potentiële energie niet betrokken, omdat de structuur aan de opleggingen geen verplaatsing ondergaat en er dus ook geen arbeid geleverd wordt.
Inwendige potentiële arbeid (vervormingsenergie)
[bewerken]We kunnen ook de arbeid geleverd door de inwendige krachten op dezelfde manier benaderen. De inwendige vervormingsenergie Av kan uitgeschreven worden als volgt (de index v duidt op inwendig):
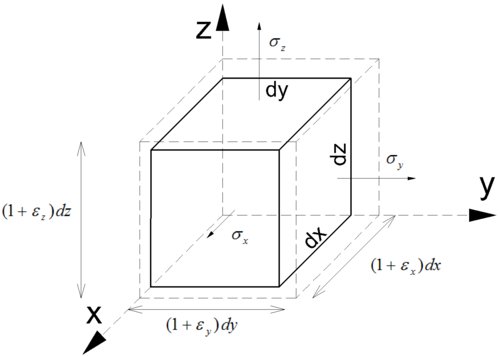
Beschouwen een elementair kubisch lichaam waarop de normaalspanningen σx, σy en σz inwerken met de rekken εx, εy, εz tot gevolg, zoals op onderstaande figuur:
De elementaire inwendige vervormingsenergie dAv van dit volume kan dan uitgeschreven worden als volgt:
Hieruit volgt dat de opgestapelde energie per volumeëenheid "U" gelijk is aan:
Indien ook de schuifspanningen inwerken op de zijvlakken van de kubus, dan zullen ook deze arbeid verrichten. Er kan aangetoond worden dat de arbeid per volumeëenheid geleverd door de schuifspanningen gelijk is aan:
Deze arbeid mag gewoon opgeteld worden bij de arbeid geleverd door de normaalspanningen. De totale inwendige arbeid (vervormingsenergie) per volumeëenheid "U" bedraagt dan:
Met de wetten van Hooke kan deze vervormingsenergie per volumeëenheid uitgeschreven worden in functie van de spanningen alleen:
Deze uitdrukking van de vervormingsenergie ligt aan de basis van de meeste theoriën voor de berekening van hyperstatische structuren. Men kan eenvoudig aantonen dat de vervormingsenergie per volemeëenheid U steeds positief of nul is.

















![{\displaystyle \delta =L.{\sqrt[{3}]{\frac {P}{EA}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d197a5032fd620b42d5b4aacceafdce27c3dd7f)





![{\displaystyle \varepsilon _{x}={\frac {\sigma _{x}}{E}}-\nu .{\frac {\sigma _{y}}{E}}-\nu .{\frac {\sigma _{z}}{E}}={\frac {1}{E}}[\sigma _{x}-\nu (\sigma _{y}+\sigma _{z})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c0d53817b47a2edb35ac6cd6e4a948bede21c88d)
![{\displaystyle \varepsilon _{y}={\frac {\sigma _{y}}{E}}-\nu .{\frac {\sigma _{z}}{E}}-\nu .{\frac {\sigma _{x}}{E}}={\frac {1}{E}}[\sigma _{y}-\nu (\sigma _{z}+\sigma _{x})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f18734705ee86ad78344dc2bd7da917f86bdca96)
![{\displaystyle \varepsilon _{z}={\frac {\sigma _{z}}{E}}-\nu .{\frac {\sigma _{x}}{E}}-\nu .{\frac {\sigma _{y}}{E}}={\frac {1}{E}}[\sigma _{z}-\nu (\sigma _{x}+\sigma _{y})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c51f6f6b04c74ebbe2499fa8300b103d0efa86d)






















![{\displaystyle \varepsilon _{x}={\frac {1}{E}}[\sigma _{x}-\nu (\sigma _{y}+\sigma _{z})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/723f817fbd4167b36b0e56f78757e84b3384af64)
![{\displaystyle \varepsilon _{y}={\frac {1}{E}}[\sigma _{y}-\nu (\sigma _{z}+\sigma _{x})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbdee01ffbfe6c6c3ce239d0db6692f14337a3fe)
![{\displaystyle \varepsilon _{z}={\frac {1}{E}}[\sigma _{z}-\nu (\sigma _{x}+\sigma _{y})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d4c846d9c685f35bc346818f16882355294e4fd)








![{\displaystyle {\begin{aligned}dA_{v}&={\frac {1}{2}}(\sigma _{x}.dy.dz).[(1+\varepsilon _{x}).dx-dx]+{\frac {1}{2}}(\sigma _{y}.dz.dx).[(1+\varepsilon _{y}).dy-dy]+{\frac {1}{2}}(\sigma _{z}.dx.dy).[(1+\varepsilon _{z}).dz-dz]\\&={\frac {1}{2}}(\sigma _{x}.dy.dz).\varepsilon _{x}.dx+{\frac {1}{2}}(\sigma _{y}.dz.dx).\varepsilon _{y}.dy+{\frac {1}{2}}(\sigma _{z}.dx.dy).\varepsilon _{z}.dz\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f46ef95aa27972fe56082dec9b80c7c02512bfcf)



