Wiskunde/Pythagoras
Uit Wikibooks
|
|
| Hoofdstukken | |
Inhoud |
[bewerk] De stelling van Pythagoras
De stelling van Pythagoras is waarschijnlijk de bekendste stelling in de wiskunde. De stelling dankt zijn naam aan de Griekse wiskundige Pythagoras. 'Zijn' stelling was overigens alleen maar nieuw voor de Grieken. In Soemerië was het resultaat al veel langer bekend. Belangrijker nog dan de kennis van de stelling was het leveren van een bewijs daarvoor; daarbij waren de Grieken (Pythagoras of een van zijn leerlingen) wel de eersten. De stelling zegt iets over de relatie tussen de rechthoekszijden en de schuine zijde van een rechthoekige driehoek.
In de rechthoekige driehoek ABC zijn de zijden a en b de rechthoekszijden. De zijde c noemen we de schuine zijde of hypotenusa.
De stelling van Pythagoras luidt:
- "In een rechthoekige driehoek is het kwadraat van de lengte van de hypotenusa gelijk aan de som van de kwadraten van de lengtes van de rechthoekszijden."
Anders geformuleerd:
- a2 + b2 = c2
De stelling van Pythagoras is een van de oudste stellingen uit de oudheid. Volgens de legende was Pythagoras zo in z'n nopjes met zijn ontdekking van de stelling dat hij een offer aan de goden bracht in de vorm van een paar ossen.
[bewerk] Bewijzen
|
|
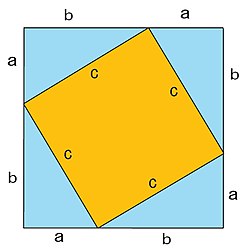
Er bestaan vele tientallen bewijzen van deze stelling. Een van de eenvoudigste vormen maakt gebruik van vier rechthoekige driehoeken, zoals in de afbeelding hiernaast. Telkens zijn een korte en een lange zijde in elkaars verlengde geplaatst. De lengte en breedte van de zijden van het vierkant zijn (a+b), dus de oppervlakte van het grote vierkant is (a+b)2. De oppervlakte is ook gelijk aan de som van de vier driehoeken (4 × ½ab) en de oppervlakte van het binnenste vierkant, dat oppervlakte c2 heeft. Dus (a+b)2=2ab + c2. |
Er is nog een makkelijk bewijs met behulp van de cosinusregel:
omdat je een rechthoekige driehoek hebt, is hoek γ altijd 90°.
[bewerk] Pythagorese drietallen
De kleinste gehele waarden die aan de stelling van Pythagoras voldoen zijn 3,4,5 (32 + 42 = 52). Uiteraard voldoet ook elk veelvoud hiervan, zoals 62 + 82 = 102.
Er zijn oneindig veel combinaties van gehele getallen die aan de vergelijking x2+y2=z2 voldoen. (5,12,13) is een andere combinatie. Deze combinaties worden ook wel Pythagorese drietallen genoemd.
[bewerk] Externe links
 |
Deze pagina is vrijgegeven onder de GNU Free Documentation License (GFDL) en nog niet onder CC-BY-SA. Klik hier voor meer informatie.
Wilt u deze tekst gebruiken onder de Creative Commons CC-BY-SA licentie? |
