Sterrenkunde van de Lokale Groep/02

Sterrenkunde van de Lokale Groep

Auteurs

Hansmuller

Even terug naar onze directe woonomgeving: ons eigen Zonnestelsel met Zon en planeten. Daarna gaan we verder van huis op reis in ons Melkwegstelsel.

Zonnestelsel

Ons Zonnestelsel lijkt op een raderwerk of klok. De verschillende planeten hebben hun eigen omlooptijd.
Hoe verder weg van de Zon (hier Sol, de Latijnse naam), hoe rustiger ze rondlopen.
Eerst de Zon (hier Sol, de Latijnse naam) en de binnenplaneten:
Mercurius (hier Mercury, de Engelse naam, omlooptijd 88 dagen ~ 1/4 jaar) en Venus (243 dagen ~ 2/3 jaar).
Dan de Aarde (Earth, 365,256 dagen = 1 jaar) en Mars (687 dagen = 1,9 jaar, bijna 2 jaar).

Nu nog de buitenplaneten Jupiter (omlooptijd 11,9 jaar ~ 12 jaar), Saturnus (Saturn, 29,5 jaar), Uranus (84 jaar) en Neptunus (Neptune, 164,9 jaar ~ 165 jaar):

Zon en planeten zien er in zichtbaar licht en op schaal ongeveer zo uit als hieronder (tussenafstanden kloppen hier niet):

Zon met zwarte, want minder hete zonnevlek
Dwergplaneten, van Sedna tot Pluto (met maantjes Charon, Styx, Nix, Kerberos en Hydra) ver weg
Gasreuzen: Neptunus, Uranus, Saturnus en Jupiter, met hun vele manen!
Aardachtige planeten: Mars met twee manen, Aarde met Maan, Venus en Mercurius.
- Tussen Jupiter en Mars loopt de schattige dwergplaneet Ceres (diameter 950 km, omlooptijd om de zon 4,6 jaar).

Nu Zon en planeten met wel de tussenafstanden op goede schaal (inner planets = binnenplaneten):

Draaiing van de aarde 's nachts

De aarde draait naar het oosten, eenmaal rond in 24 uur.
De sterrenbeelden Grote Beer (koekepan) en Cassiopeia (de W) lijken 's nachts om de stilstaande Poolster te draaien. De Poolster staat boven de Noordpool.
Bij lange belichting van een foto 's nachts zien we de schijnbare sporen van de sterren rond de Poolster, omdat wijzelf eronder door draaien. De twee rechte kruisende lijnen zijn langskomende satellieten zo te zien.

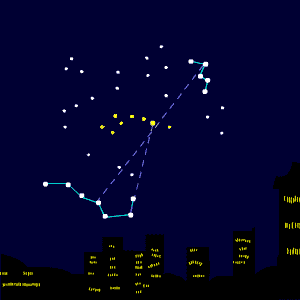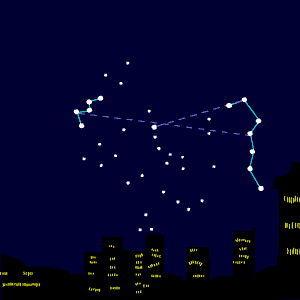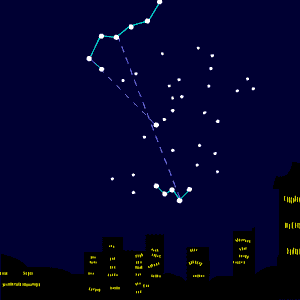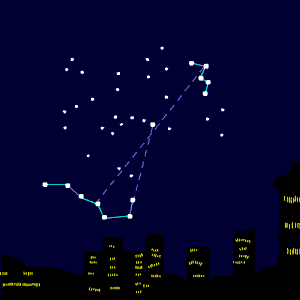
Meer sterrenbeelden

Als we sterren aan de hemel zien, zijn die van onze eigen Melkweg. Bijvoorbeeld sterrenbeeld Orion:

Wintersterrenbeelden

Afstanden in het heelal

Lichtsnelheid, lichtjaar en meetmethoden

Lichtsnelheid in luchtledig en lucht = 300.000 km/s.
Afstand Aarde-Zon = 150 miljoen km.

Licht doet hier 500 seconden over, 500/60 = 8 minuten en 20 seconden.
Dus we zien de zon zoals die er zolang geleden uitzag.

1 lichtjaar = afstand die licht aflegt in een jaar = 365,25 dagen x 24 uur/dag x 3600 seconden/uur x 300.000 km/s = 9467 miljard kilometer.
Vergelijk voor de grap:
- 1 wandeldag = 8 uur x 5 km/uur = 40 km (afgelegde afstand in 1 dag wandelen).
- 1 wandeljaar = zeg 350 wandeldagen = 350 x 40 km = 14.000 km (1 jaar wandelen).
- 1 lichtjaar = 9467 miljard km/14.000 km wandeljaren = 0,676 miljoen wandeljaren.
- 1 wandelleven = zeg 50 wandeljaar = 700.000 km (50 jaar wandelen)

Dus

1 lichtjaar = 9467 miljard km/700.000 km = 13,5 duizend levens wandelen.

Het bepalen van afstanden in het heelal kan op verschillende manieren: afstand tot de Maan met zon- en maansverduisteringen, en afstand tot de Zon met overgangen van planeten voor de Zon langs. Andere methoden zijn met opvallende veranderlijke sterren van bekende helderheden: de Cepheïden en RR Lyrae sterren. Door de waargenomen helderheid te vergelijken met de waargenomen helderheid vind je hun afstand. Verder kunnen grote afstanden berekend worden dankzij bekende helderheden van supernovae type 1A (SN1A), bolhopen, en met de Tully–Fisher-wet, de kosmologische roodverschuiving en voor dichterbij.... de methode van de parallax.
Als je een tweede keer schuin naar iets kijkt, vind je de afstand...

Afstanden meten met parallax: verspringing van de achtergrond

Als je kijkt waar een nabije ster aan de hemel staat met een halfjaar tussentijd, blijkt dat die verspringt tegen de vaste achtergrond.
(Dit zelfde effect gebruiken wij om met onze twee ogen tegelijk diepte te zien.)
Met de hoek van de verspringing van de ster tegen de achtergrond en de afstand Aarde-Zon kan de afstand Zon-ster bepaald worden.
De figuur geeft een Frans voorbeeld met een ster voor het sterrenbeeld de Grote Beer, waargenomen in december en juni.
Als de achtergrond van sterren toch beweegt, werkt deze methode natuurlijk niet...
En voor een verre ster wordt de hoek van de verspringing van de achtergrond te klein om goed te meten.

Een Frans plaatje. Als we dezelfde ster in december en juni waarnemen vanuit onze aardbaan om de Zon, blijkt de ster tegen de achtergrond van sterrenbeeld de Grote Beer verschoven te zijn. Met de grootte van dit effect - de parallax van de ster - kunnen we de afstand van de ster bepalen.

Afstand Aarde - Zon = 1 AU (Astronomical Unit, Astronomische eenheid = 150 miljoen kilometer).
D = Afstand Zon - Ster is onbekend en willen we weten.
Hoek P = Halve hoek van de verspringing van de achtergrond, kunnen we meten.
Dan weten we uit de goniometrie de verhouding van de driehoekszijden 1 AU en D:
Tangens (hoek P) = 150 miljoen km / D, dus antwoord wordt:
Afstand D = 150 miljoen kilometer / tangens (hoek P).
De afstand D wordt uitgedrukt in parsecs = 3,26 lichtjaar.
Met de Hubble Ruimtetelescoop kun je zo afstanden tot minstens 7500 lichtjaar bepalen.

Een Engels plaatje. **De verschuiving - parallax - gemeten met de Hubble Space Telescope kunnen we gebruiken om nog grotere afstanden te bepalen dan met kleine telescopen.**

Klik hier voor het vervolg