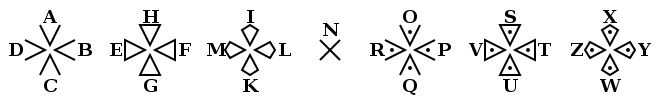Geheimschrift/Alfabetten
Er zijn veel soorten geheimschrift. In dit hoofdstuk kijken we naar wat we met een mooi woord "mono-alfabetische substituties" noemen. Dat wil zeggen dat elke letter door 1 ander symbool vervangen wordt.
Caesargeheimschrift
[bewerken]Een van de oudste geheimschriften is de substitutie van het Caesarcijfer.
In deze code wordt elke letter vervangen door een volgende letter uit het alfabet. Dus A wordt vervangen door B, B wordt vervangen door C, enzovoorts, tot en met de Z die vervangen wordt door de A.
Het is gemakkelijk en snel te doen. Sommige mensen gebruiken het voor hun dagboek. Als iemand een willekeurige bladzij open slaat, zal deze niet direct snappen wat er staat. Met wat oefening schijnen mensen dit (bijna) net zo snel te schrijven als normaal schrift.
Julius Caesar gebruikte dit systeem, maar dan met 3 plaatsen opschuiven. Dus A wordt D, B wordt E, etc. Dat wordt ook wel ROT-3 genoemd. ROT staat dan voor ROTeren. Een speciaal geval is ROT-13. Dan schuiven alle letters 13 plaatsen op. Dus twee keer uitvoeren levert de oorspronkelijke tekst op!
Ontcijferen
[bewerken]Wanneer je het bericht in geheimschrift binnenkrijgt, ga je zoveel plaatsen in het alfabet terug als de vercijferaar plaatsen vooruit is gegaan.
Cryptoanalyse
[bewerken]Wanneer je een bericht in handen krijgt waarvan je vermoedt dat de verzender het Caesargeheimschrift heeft gebruikt, kun je het bericht overschrijven. Vervolgens schrijf je voor elke letter in het bericht het alfabet naar beneden uit.
Voorbeeld: het bericht luidt: EMCB. Je schrijft dan op:
EMCB FNDC GOED HPFE IQGF etc
Op de derde regel verschijnt het woordje 'GOED', dus je weet dan dat je 2 plaatsen moet op schuiven.
Er zijn andere manieren om het bericht te 'kraken', daarover meer aan het einde van dit hoofdstuk.
Sleutelalfabet
[bewerken]Het Caesargeheimschrift werkt met het standaard alfabet. In deze variant gebruiken we een alfabet dat door een sleutelwoord wordt veranderd.
Het recept is eenvoudig: neem een woord, bijvoorbeeld “zandbak”. Haal daar de herhaalde letters uit. In ons voorbeeld houden we dan “zandbk” over. Schrijf dat op en zet de andere letters van het alfabet er achter. Schrijf het standaard alfabet er boven.
ABCDE FGHIJ KLMNO PQRST UVWXY Z ZANDB KCEFG HIJLM OPQRS TUVWX Y
Zoek nu in elke letter uit het te versleutelen bericht op in de bovenste regel en vervang het door de letter daaronder.
Dus:
“DIT BERICHT IS NIET MOEILIJK”
wordt dan:
"DFS ABQFNES FR LFBS JMBFIFGH"
Het woord “Zandbak” wordt het sleutelwoord genoemd. Door regelmatig het sleutelwoord te veranderen, wordt een bericht iets (een heel klein ietsje) lastiger te ontcijferen.
Ontcijferen
[bewerken]Degene voor wie het bericht bestemd is, schrijft het gewone alfabet en het sleutelalfabet onder elkaar, en zoekt elke letter uit het gecodeerde bericht op in het sleutelalfabet. De letter uit het gewone alfabet is dan de oorspronkelijke letter.
Cryptoanalyse
[bewerken]Het bericht ziet er misschien mysterieus uit, maar het kent veel zwakheden. Een aantal opvallende zwakheden zijn:
- a) Je ziet dat aan het eind van het alfabet de oorspronkelijke letter uit het bericht en de gecodeerde letter in het alfabet dicht bij elkaar staan. Doordat het woord ‘zandbak’ een ‘z’ bevat, verschillen ze nog iets, maar als dat niet het geval is, blijven de letters w, x, y en z vaak onveranderd.
Dus als je een gecodeerd bericht in handen krijgt, en je ziet een ‘w’, weet je dat dit waarschijnlijk een ‘v’, ‘w’ of ‘x’ is geweest. Dat is nog te verhelpen door de rest van het alfabet achterstevoren te schrijven, dus: zandb kyxwv utsrq pomlj ihgfe c Maar er zijn nog meer problemen.
- b) De lengte van de woorden is onveranderd gebleven. Vooral korte woorden zijn een aanwijzing. Als je vaak een woord van 2 letters voor een lang woord ziet staan, dan is ‘de’ een voor de hand liggende gok.
De standaard werkwijze om de ontsleutelaar dit voordeel te ontnemen, is om de woorden na het versleutelen te groeperen in groepjes van 5 letters.
- "DFSAB QFNESF RFLBS JMBFI FGH"
ziet er al lastiger uit dan:
- "DFS ABQFNES FR LFBS JMBFIFGH"
Het groeperen van gecodeerde berichten in groepen van 5 letters is in de loop van de eeuwen standaard werkwijze geworden. Iets anders wat in de loop der eeuwen gebruikelijk is geworden, is het weglaten van leestekens. Een punt ‘,’ geeft keurig aan waar een zin eindigt. En als je een komma (‘,’) ziet, weet je dat de kans groot is dat daarna een van de woordjes ‘en’, ‘of’ of ‘maar’ volgt. Door de leestekens weg te laten, ontnemen we de ontcijferaar dit kleine voordeeltje.
- c) Totdat de sleutel verandert, wordt een letter altijd door dezelfde letter vervangen. In het Nederlands en het Engels zijn de ‘e’ en de ‘n’ de meest voorkomende letters. Neem maar eens een paragraaf van vijf of meer regels en tel hoeveel a’s, b’s enzovoorts er in die tekst voorkomen. Je zult zien hoe snel de ‘e’ en de ‘n’ er uit springen.
Om zo’n bericht als hierboven te ontcijferen, kun je beginnen met te tellen hoe vaak elke letter voorkomt. Je haalt er dan al snel de ‘e’ en de ‘n’ uit.
Het Caesarschrift en bovenstaande sleutelalfabet zijn de bekendste voorbeelden van wat we een mono-alfabetische substitutie noemen.
Andere voorbeelden van monoalfabetische substituties zijn
Het Brailleschrift en het Morse alfabet zijn niet bedoeld als geheimschriften. Wel vallen ze onder de mono-alfabetische substituties.
- Kaderschrift of Rozenkruisersgeheimscrhift.
Rozenkruisersgeheimschrift
[bewerken]Het Rozenkruisersgeheimschrift, ook wel tempeliersgeheimschrift, of vrijmetselaarsalfabet genoemd, kent verschillende vormen. Het gemeenschappelijke is dat het uit gaat van een alfabet, dat is ingedeeld in verschillende vakjes. Bijvoorbeeld:
Met behulp van de voorbeeldsleutel, de gegeven diagram, kan de tekst "X marks the spot" als volgt in versleutelde tekst worden weergegeven:
De ridderorde van de tempeliers zou gebruik hebben gemaakt van een versleuteling gebaseerd op het Maltezer kruis[1]
Er zijn, zoals uit bovenstaande blijkt, verschillende vormen in gebruik geweest. Niets verhindert je om een eigen variant te bedenken. Als kleine extra moeilijkheid kun je ook hier, net als bij het caesargeheimschrift, het alfabet mengen op basis van een sleutelwoord:

Om dit format te gebruiken, geef met de positie van een punt aan of de linker, middelste of de rechter van de drie letters in het vakje moet worden gebruikt. De tekst "ZEG NIETS" wordt dan:
Atbash geheimschrift
[bewerken]Het Atbash geheimschrift neemt als sleutelalfabet het gewone alfabet maar achterstevoren geschreven. Het schijnt oorspronkelijk op het Hebreeuwse alfabet gebaseerd. Men neemt aan dat het ouder is dan Egyptische geheimschriften[2]).
Affine geheimschrift
[bewerken]Het ‘Affine geheimschrift’ gebruikt getallen, en gaat een stap verder dan a=1 b=2 … z=26. We beginnen daar wel mee:
- “geheim” wordt 7 5 8 5 9 13.
Vervolgens rekenen we hiermee volgens de formule:
- F(x)=(ax+b) mod 26.
Module 26 wil zeggen: trek er net zo vaak 26 van af totdat we lager dan 26 uitkomen, oftewel totdat we een getal tussen de 0 en de 25 over houden. De a en b vormen daarbij onze sleutel. Stel dat we zouden kiezen dat a = het nummer van de dag in de week (ma=1, zo=5) en b is de dag in de maand. Dus als we bovenstaande bericht zouden coderen op dinsdag de 18e, wordt de functie f(x)=(2x+18) mod 26.
- f(7) = (2*7 + 18) mod 26 = 32 mod 26 = 6
- f(5) = (2*5 + 18) mod 26 = 28 mod 26 = 2
- f(8) = (2*8 + 18) mod 26 = 34 mod 26 = 8
- f(5) = (2*5 + 18) mod 26 = 28 mod 26 = 2
- f(9) = (2*9 + 18) mod 26 = 36 mod 26 = 10
- f(13) = (2*13 + 18) mod 26 = 44 mod 26 = 18
De laatste stap is dan om deze getallen weer door een letter te vervangen:
- FBHBJR
Maar we zien hier gelijk al een probleempje opdoemen: alle verkregen getallen zijn even, dus er zijn maar 13 verschillende uitkomsten. f(a)=f(1)=2+18=20 f(n)=f(2*14+18 mod 26) = 28+18 mod 26 = 46 mod 26 = 20 Zo geven de letters a en n dezelfde gecodeerde waarde, dus degene die het bericht kent, zal voor elke letter uit twee verschillende bronletters moeten kiezen, ook degene voor wie het bericht kent. De letter ‘a’ in de formule zal dus in elk geval een oneven waarde moeten hebben.
Cryptonalayse
[bewerken]Cryptoanalyse is het woord dat we gebruiken voor het ontcijferen van berichten die niet voor ons bedoeld zijn. Degene die een geheimschrift probeert te 'kraken', wordt een cryptoanalist of codebreker genoemd.
Hoe ontcijfer je een mono-alfabetische substitutie?
De eerste stap van cryptoanalyse is het tellen van de frequentie van de letters. Komen de E en de N het meest voor? Dan is het bericht vrijwel zeker in het Nederlands, Engels of Duits, en is er geen substitutie maar een transpositie uitgevoerd. Zie daarvoor het volgende hoofdstuk. Steken er 2 andere letters met kop en schouders boven de anderen uit? Dan zal de crypto analist een gok voor de taal en de letters E en N maken.
De cryptoanalist zal de boodschap uitschrijven met een blanko regel er tussen. Daar zet hij de vermoedelijke E en de N onder de letters die letters die het vaakst voorkomen. Als er veel tekst beschikbaar is, kan hij nog een paar letters raden. Daarna is het handig als hij bepaalde woorden kan raden. Wat weet hij over de schrijver? Heeft die met zijn naam ondertekend? Begint er een bericht met iets als "beste Piet"? Als de oorspronkelijke woordlengte in tact is gelaten, dan maakt dat het gemakkelijk met korte woordjes als 'de', 'het', 'of', 'in', 'en' etc.
| Letter | Percentage |
|---|---|
| e | 18,91% |
| n | 10,03% |
| a | 7,49% |
| t | 6,79% |
| i | 6,50% |
| r | 6,41% |
| o | 6,06% |
| d | 5,93% |
| s | 3,73% |
| l | 3,57% |
| g | 3,40% |
| v | 2,85% |
| h | 2,38% |
| k | 2,25% |
| m | 2,21% |
| u | 1,99% |
| b | 1,58% |
| p | 1,57% |
| w | 1,52% |
| j | 1,46% |
| z | 1,39% |
| c | 1,24% |
| f | 0,81% |
| x | 0,040% |
| y | 0,035% |
| q | 0,009% |
Bron: https://onzetaal.nl/taalloket/letterfrequentie-in-het-nederlands[3]
Hoe veilig zijn deze geheimschriften?
[bewerken]De eerste wet van de cryptografie luidt: Een geheimschrift moet veilig genoeg zijn om het geheim te beschermen tot het moment dat het niet belangrijk genoeg meer is.
Het Caesargeheimschrift was in de tijd van Julius Caesar waarschijnlijk veilig genoeg tegen Gallische en Germaanse stammen. Daar was het analfabetisme hoog, al steeg het percentage mensen dat kon lezen en schrijven naarmate gebieden langer onder Romeinse controle stonden. En degenen die konden lezen en schrijven, hadden waarschijnlijk weinig kennis van geheimschriften.
Maar bij een Romeinse burgeroorlog lag dat anders. Daar waren aan beide kanten Legioenen betrokken waarvan de officieren mogelijk het geheimschrift kenden.
Al-Qalqashandi publiceerde in 1412 het laatste deel vanṢubḥ al-Aʿshá fī Ṣināʿat al-Inshā, waarin hij de methode publiceerde om op basis van letter frequenties elke mono-alfabetische substitutie aan te pakken. Hij baseerde zich daarbij deels op eerder werk van Ibn al-Durayhim (1312–1359). Sinds die tijd is elk geheimschrift dat zich baseert op een 1:1 vervanging van letters onveilig. Ze worden nog vaak gebruikt, maar dan als puzzel met de bedoeling om opgelost te worden, in tijdschriften, of in escape rooms.
Toch speelde een vorm van een eenvoudige substitutie rond 1900 nog een rol. Tijdens de w:Boerenoorlogen (1880-1881 en 1899-1902) hadden de Britse officieren het idee dat ze geen goede geheimschriften ter beschikking hadden. De officieren schreven daarom onderling hun berichten in het Engels, maar met Griekse letters. Omdat veel Britse officieren het Griekse alfabet meester waren, terwijl maar weinig Boeren dit kenden, ging dat vaak goed.
Tot slot nog een voorbeeld van hoe onveilig mono-alfabetische substituties zijn. Toen in Nederland de Binnenlandse Veiligheidsdienst nog bestond, hield deze open dagen. Het publiek was dan welkom. Bezoekers werden uitgedaagd een eenvoudige, niet te korte, boodschap overeenkomstig bovenstaande principes te coderen. Een van de cryptoanalisten van de BVD las ze bij het zien gewoon direct in het Nederlands op.
De logische vervolgvraag is dan: wat zijn dan wel veiliger methodes? De antwoorden hierop varieerden in de loop van de tijd:
- transposities in plaats van substituties
- polyalfabetische substituties
- substituties van 2-lettergroepen, 3- lettergroepen en van hele woorden
- onzichtbare geheimschriften
- combinaties van bovenstaande
- blokgeheimschriften
In Hoofdstuk 2 gaan we dieper in op de transposities, omdat ook die een heel oude vorm van geheimschriften vormen.