Sterkteleer/Bepaling van de snedekrachten

Algemeen

Uit de betrekkingen (2.1.3) en (2.1.4) halen we volgende verbanden voor de x-component:

$R_{1.inw.x}+\sum X_{1i}=0$

$\,R_{2.inw.x}=-R_{1.inw.x}$

$=>R_{2.inw.x}=\sum X_{1i}$

We stellen vast dat de som van de x-componenten van de krachten die inwerken op deel 1, gelijk is aan de x-component van snedekracht door deel 1 uitgeoefend op deel 2. Deze x-component van de snedekracht is de normaalkracht N op de snede. We kunnen voor elke compenent van de snedekracht analoge formules opstellen.

Bepaling van snedekrachten in een willekeurige snede (3.1)

• De snedekrachten inwerkend op het deel links van een willekeurige snede zijn gelijk (statisch gelijkwaardig) aan de som van uitwendige krachten die inwerken op het deel rechts van de snede. Rechts en links kunnen hier omgewisseld worden.

$N=\sum X_{i}$ $T_{y}=\sum Y_{i}$ $T_{z}=\sum Z_{i}$ $M_{t}=\sum M_{ix}$ $M_{y}=\sum M_{iy}$ $M_{z}=\sum M_{iz}$

Hierin is:

$N\,,T_{y}\,,T_{z}$ : de x, y en z-component van de snedekracht op het linkerdeel (N) $X_{i}\,,Y_{i}\,,Z_{i}$ : de x, y en z-component van de uitwendige krachten op het rechterdeel (N) $M_{t}\,,M_{y}\,,M_{z}$ : de x, y en z-component van het snedemoment op het linkerdeel (N.m) $M_{ix}\,,M_{iy}\,,M_{iz}$ : de x, y en z-component van de uitwendige momenten op het rechterdeel (N.m) linker- en rechterdeel kunnen omgewisseld worden

Voorstelling van de snedekrachten: N T M - diagramma's

In de sterkteleer is het niet zozeer de bedoeling om de snedekrachten in één willekeurige snede van een balk te kennen. Om constructies te berekenen is het aangewezen het verloop van de snedekrachten over de volledige balk te kennen. Hiervoor maakt men gebruik van zogenaamde "N T M - diagramma's", een grafische voorstelling van de normaalkracht N, de dwarskrachten T en de momenten M. Hoe deze NTM-diagramma's worden opgesteld wordt duidelijk gemaakt aan de hand van enkele voorbeelden. Aangezien de NTM-diagramma's een zeer belangrijk werkinstrument zijn in de sterkteleer die snel inzicht geven in de interne krachtswerking in een structuur, worden de voorbeelden zeer gedetailleerd uitgewerkt.

De lezer wordt ook uitgenodigd de bijhorende oefeningen uit te proberen om vertrouwd te raken met deze diagramma's en hun achterliggende betekenis.

Voorbeeld 1 - Normaalkrachten

We beschouwen een balk AB waarop 2 krachten F=10kN inwerken volgens de aslijn in de punten A en B, zoals op onderstaande figuur.
Merk op dat de staaf in evenwicht is, vermits de vectorsom van alle inwerkende krachten gelijk is aan 0 (zie formule 2.1.1).

Om de snedekrachten te bepalen maken we een willekeurige snede S, waardoor we de balk verdelen in een linker- en een rechterdeel.

We kunnen nu zowel het evenwicht voor het linker- als het rechterdeel uitschrijven volgens de formules (3.1).

Voor het linkerdeel geldt dat de snedekrachten statisch gelijkwaardig moeten zijn met de krachten die in werken op het rechterdeel. Op het het rechterdeel werkt enkel een kracht $\,F=10kN$, volgens de aslijn in het punt B.
De enige kracht die optreedt is een normaalkracht, aangezien alle andere componenten van de uitwendige krachten gelijk zijn aan 0. Er zijn geen dwarskrachten of momenten.
We stellen de normaalkracht in de snede inwerkend op het linkerdeel van de balk voor als $\,N_{L}$

Er geldt nu hetvolgende eenvoudige verband tussen de snedekracht inwerkend op het linkerdeel en de uitwendige krachten op het rechterdeel: $\,N_{L}=F=10kN$

Voor het rechterdeel gaat de dezelfde redenering op zodat $\,N_{R}=F=10kN$

Merk op dat vectorieel gezien geldt: $\,{\vec {N_{L}}}=-{\vec {N_{R}}}$, zoals vooropgesteld in formule (2.1.4). Wegens dit verband kunnen we ons beperken om enkel de snedekrachten op ofwel het linkerdeel, of wel het rechterdeel te berekenen. Hierbij zullen we trachten steeds dit deel uit te rekenen waarop de krachtswerking het minst ingewikkeld is.

We hebben nu de snedekrachten bepaald in Snede S. Het is eenvoudig in te zien dat deze zelfde snedekrachten niet enkel optreden in de getekende snede S, maar in ook in elke andere mogelijke snede in de balk AB.

Het NTM-diagramma is in dit geval enkel een normaalkrachten-diagramma of N-diagramma, aangezien de overige snedekrachten gelijk zijn aan 0. We tekenen dit diagramma door over de ganse balk aan te duiden dat de snedekracht gelijk is aan N = 10 kN.

Aangezien de optredende normaalkracht een trekkracht is (zie verder bij tekenconventies NTM-diagramma's), duiden we dit aan door een (+) te plaatsen in het N-diagramma en het N-diagramma aan de onderkant van de balk AB te tekenen.

We kunnen aan de hand van het N-diagramma in één oogopslag zien dat over de ganse lengte van de balk AB in elke snede een trekkracht N = 10 kN optreed.

Voorbeeld 2 - Ingeklemde balk

Als tweede voorbeeld beschouwen een balk AB, die ingeklemd is in punt A, en waarop een kracht F inwerkt in het punt B, zoals in de figuur hieronder. Gevraagd wordt de NTM-diagramma's te tekenen.

Stap 1: Bepaling van de uitwendige krachten - vrijmaken

Vooraleer we aan NTM-diagramma's denken, dienen we eerst alle uitwendige krachten te bepalen, volgens de regels van de statica. We maken hiervoor gebruik van de techniek van het vrijmaken.

• stap 1a: Referentie-assenkruis
  

Het is aangewezen vanaf het begin een refentie-assenkruis in te stellen. Zoals hoger vermeld leggen we de x-as evenwijdig met de aslijn en de y-as loodrecht naar beneden gericht. Aangezien dit een 2-dimensionaal probleem is een z-as niet echt noodzakelijk. Voor een goed begrip van wat volgt, beelden we ons toch een z-as in, loodrecht op het xy-vlak, naar de lezer toe gericht.

• stap 1b: Opzoeken en aanduiden van alle uitwendige krachten, inclusief de verbindingskrachten / reactiekrachten
  

Punt A
De balk is ingeklemd in het punt A. Een inklemming is een verbinding met de omgeving, die zowel horizontale krachten, vertikale krachten als een moment kan opnemen. Volgens de 3e wet van Newton (actie=reactie) zijn de krachten die de balk uitoefent op de inklemming, even groot en tegensteld aan de krachten die de inklemming uitoefent op de balk. Deze krachten uitgeoefend door de inklemming op de balk zijn zogenaamde verbindingskrachten (zie Structuren en krachten); en deze verbindingskrachten zijn te beschouwen als uitwendige krachten op de balk.

Een verbindingskracht met de omgeving of een ander structuuronderdeel wordt in de sterkteleer aangeduid met de term reactiekracht.

Vermits punt A een inklemming is, hebben we te maken met een reactiekracht en een reactiemoment. De reactiekracht kan ontbonden worden in een component volgens de x-as en een component volgens de y-as. Het reactiemoment moet een hoekverdraaiing in het xy-vlak tegengaan, en is dus een moment rond de z-as.

Punt B
In punt B hebben we te maken met een uitwendige kracht F = 10 kN, gelegen in een hoek θ ten opzichte van de x-as. We kunnen deze kracht ook ontbinden in een component volgens de x-as en de y-as:

$\,F_{x}=F_{H}=F\cos \theta =10\times 3/5=6kN$

$\,F_{y}=F_{V}=F\sin \theta =10\times 4/5=8kN$

• stap 1c: Schematische voorstelling - vrijmaken
  

We duiden alle externe krachten aan op een schematische voorstelling zoals hieronder.

• stap 1d: Berekenen uitwendige krachten
  

Door de evenwichtvergelijkingen van de statica (2.1.2) toe te passen kunnen we nu eenvoudig alle externe krachten bepalen:

Horizontaal evenwicht

$\,-R_{AH}+F_{H}=0\,=>R_{AH}=F_{H}=6kN$

Vertikaal evenwicht

$\,-R_{AV}+F_{V}=0\,=>R_{AV}=F_{V}=8kN$

Momentenevenwicht rond punt B

$\,-M_{A}+R_{AV}.L=0\,=>M_{A}=R_{AV}.L=8kN\times 10m=80kNm$

Stap 2: Bepaling van de snedekrachten - opstellen NTM-diagramma's

Nu alle uitwendige krachten zijn berekend, kunnen we overgaan tot het berekenen van de snedekrachten. We beschouwen hiertoe de willekeurige snede S, waarop de snedekrachten $\,N,T_{y}$ en $\,M_{z}$ werkzaam zijn. We beschouwen het rechterdeel, omdat hier maar 2 uitwendige krachten inwerken. De externe krachten inwerkend op het rechterdeel zijn statisch gelijkwaardig met de snedekrachten op het linkerdeel, en kunnen we berekenen met de formules (3.1)

Horizontaal evenwicht

$\,N=F_{H}=6kN$

Vertikaal evenwicht

$\,T_{y}=F_{V}=8kN$

Momentenevenwicht in de snede

$\,M_{z}=0\times F_{H}-(L-x)\times F_{V}=-F_{V}\times (L-x)$

Merk op dat de kracht $\,F_{V}$ een moment levert ten opzichte van de snede S met hefboomsarm (L-x) De hefboomsarm van de kracht $\,F_{H}$ is gelijk aan 0 aangezien de werklijn van de kracht $\,F_{H}$ door het zwaartepunt van de snede S loopt. Net zoals in voorbeeld 1 zijn de uitdrukkingen geldig voor alle mogelijke snedes S, zodat we met de berekende snedekrachten de NTM-diagramma's kunnen opstellen.

De buigmomenten worden in het M-diagramma steeds uitgezet aan de "uitgerokken zijde" van de balk, zoals op onderstaande figuur te zien is dit in dit geval de bovenzijde van de balk.

We kunnen op basis van de NTM-diagramma's onmiddellijk vaststellen dat:

• De normaalkracht N over de hele lengte van de balk gelijk is aan $\,F_{H}=6kN$.
• De dwarskracht T over de hele lengte van de balk gelijk is aan $\,F_{V}=8kN$.
• Het buigmoment M varieert lineair over de lengte van de balk volgens de formule $\,M_{z}=-F_{V}\times (L-x)$, met een maximum van -80 kNm in punt A (x=0 invullen in de uitdrukking voor M) en het moment is gelijk aan 0 in punt B (x=L invullen in de uitdrukking voor M).
• De balk wordt inwendig het zwaarst belast aan de inklemming ter hoogte van punt A.

Het opsporen van de zwaarst belaste snede in een structuur is één van de fundamentele zaken voor de berekening van structuren . Bij het ontwerp van een constructieonderdeel is één van de eerste vereisten dat het constructieonderdeel alvast in zijn zwaarst belaste snede sterk genoeg is om aan de inwendige krachten te weerstaan.

Een handigheidje voor een snelle eerste controle of de berekende uitdrukkingen voor de snedekrachten correct zijn: controleer de snedekrachten aan de opleggingen en vergelijk deze met de berekende reactiereactiekrachten in die opleggingen. In dit voorbeeld moeten de snedekrachten in punt A in grootte gelijk zijn met de overeenkomstige reactiekrachten in punt A. De snedekrachten in punt A zijn gelijk aan 6kN, 8kN en 80kNm, en dit zijn ook de waarden van de reactiekrachten in punt A.

Tekenconventies bij NTM-diagramma's

Zoals hoger uiteengezet zijn de snedekrachten op het linker en rechterdeel van de snede vectorieel tegengesteld. Om deze toch éénduidig in een NTM-diagramma te kunnen voorstellen, zijn afspraken betreffende tekenconventies noodzakelijk.

Opgelet: De tekenconventies hieronder hangen samen met hoe het assenkruis geplaatst wordt en zijn niet meer dan afspraken tussen auteur en lezer. Hoewel de hier gebruikte tekenconventies in de meeste literatuur en cursussen gebruikt worden, zijn ze niet universeel geldig. Dit sluit niet uit dat in andere literatuur andere tekenconventies voor NTM-diagramma's worden gebruikt.

Normaalkrachten

• Trek

- Het N-diagramma en de snedekracht zijn positief

- Het N-diagramma wordt aan de positieve y-as uitgezet.

• Druk

- Het N-diagramma en de snedekracht zijn negatief.

- Het N-diagramma wordt aan de negatieve y-as uitgezet.

Dwarskrachten

Een rotatie in positieve zin, is een rotatie waarbij de positieve x-as in de richting van de positieve y-as roteert. In het hier gebruikte assenkruis komt dit overeen met wijzerzin.

• De dwarskrachten willen het balkdeel een rotatie in positieve zin geven.

- Het T-diagramma en de snedekracht zijn positief

- Het T-diagramma wordt aan de positieve y-as uitgezet.

• De dwarskrachten willen het balkdeel een rotatie in negatieve zin geven.

- Het T-diagramma en de snedekracht zijn negatief

- Het T-diagramma wordt aan de negatieve y-as uitgezet.

Buigmomenten

• Een buigmoment wordt steeds uitgezet aan de uitgetrokken zijde van het balkdeel.
• Een buigmoment is positief als het balkdeel met positieve y-coördinaat uitgerokken wordt.
• Een buigmoment is negatief als het balkdeel met negatieve y-coördinaat uitgerokken wordt.

Wringmomenten

Wringmomenten veroorzaken een rotatie van een balkdeel in het yz-vlak, rond de x-as.

• Een positief wringmoment wil het balkdeel met positieve y-coördinaten een rotatie geven richting positieve z-coördinaat. Een positief wringmoment wordt uitgezet aan de positive y-as (of z-as).
• Een negatief wringmoment wil het balkdeel met negatieve y-coördinaten een rotatie geven richting positieve z-coördinaat. Een negatief wringmoment wordt uitgezet aan de negatieve y-as (of z-as).

Voorbeeld 3 - 3-dimensionale structuur met wringmoment

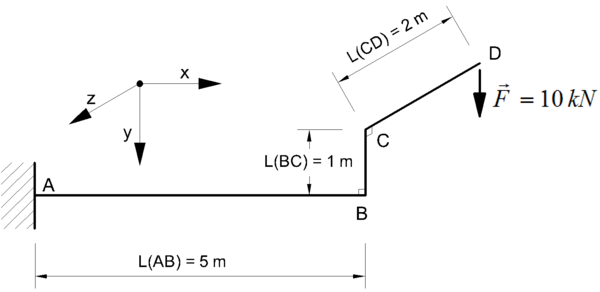
Als derde voorbeeld beschouwen een balk ABCD, die ingeklemd is in punt A, en waarop een kracht F van 10kN volgens de y-as inwerkt in het punt D, zoals in de figuur hieronder. Balkdeel AB ligt evenwijdig aan de x-as, balkdeel BC ligt evenwijdig aan de y-as, balkdeel CD ligt evenwijdig aan de z-as. Gevraagd wordt de NTM-diagramma's te tekenen.

Stap 1: Bepaling van de uitwendige krachten - vrijmaken

• stap 1a: Referentie-assenkruis
  

Het globaal referentie-assenkruis wordt geplaatst zoals in bovenstaande figuur. Bij de snedekrachten (stap 2) zullen we per balkdeel "lokale" assenkruizen vastleggen die mee varieren met de aslijn van de balk, zoals in hoofdstuk 2 werd uiteengezet.

• stap 1b: Opzoeken en aanduiden van alle uitwendige krachten, inclusief de verbindingskrachten / reactiekrachten
  

Punt A
De balk is ingeklemd in het punt A en de oplegging levert een reactiekracht ${\vec {R_{A}}}=(R_{Ax},R_{Ay},R_{Az})$ en een reactiemoment ${\vec {M_{A}}}=(M_{Ax},M_{Ay},M_{Az})$

Punt D
In punt D hebben we te maken met een uitwendige kracht ${\vec {F}}=(F_{x},F_{y},F_{z})=(0,10kN,0)$, gelegen volgens de positieve y-as en met positievector ${\vec {r}}_{AF}=(L_{AB},-L_{BC},-L_{CD})=(5m,-1m,-2m)$.

• stap 1c: Schematische voorstelling - vrijmaken
  

We duiden alle externe krachten aan op een schematische voorstelling zoals hieronder.

• stap 1d: Berekenen uitwendige krachten
  

Door de evenwichtvergelijkingen van de statica (2.1.2) in het globaal assenkruis toe te passen kunnen we nu eenvoudig alle externe krachten bepalen:

Horizontaal evenwicht

$\,-R_{Ax}+F_{x}=0\,=>R_{Ax}=F_{x}=0kN$

Vertikaal evenwicht

$\,-R_{Ay}+F_{y}=0\,=>R_{Ay}=F_{y}=10kN$

Evenwicht volgens de z-as

$\,-R_{Az}+F_{z}=0\,=>R_{Az}=F_{z}=0kN$

Momentenevenwicht in punt A rond de x-as

$\,-M_{Ax}-F_{y}.L_{CD}=0\,=>M_{Ax}=-F_{y}.L_{CD}=-10kN\times -2m=20kNm$

Momentenevenwicht in punt A rond de y-as

$\,-M_{Ay}=0kNm$

Momentenevenwicht in punt A rond de z-as

$\,-M_{Az}+F_{y}.L_{AB}=0\,=>M_{Az}=F_{y}.L_{AB}=10kN\times 5m=50kNm$

Stap 2: Bepaling van de snedekrachten - opstellen NTM-diagramma's

Voor het berekenen van de snedekrachten plaatsen we per balkdeel een lokaal assenkruis volgens de aslijn van dat balkdeel. We beschouwen het rechterdeel, omdat hier enkel de kracht F inwerkt. De externe krachten inwerkend op het rechterdeel zijn statisch gelijkwaardig met de snedekrachten op het linkerdeel, en kunnen we berekenen met de formules (3.1)

Balkdeel AB (lokaal assenkruis is gelijk aan globaal assenkruis)

Horizontaal evenwicht

$\,N=F_{x}=0kN$

Vertikaal evenwicht

$\,T_{y}=F_{y}=10kN$

Evenwicht volgens z-as

$\,T_{z}=F_{z}=0kN$

Wringmoment rond x-as

$\,M_{t}=(-L_{BC})\times F_{z}-(-L_{CD})\times F_{y}=-1\times 0-(-2)\times 10=20kNm$

Buigmoment rond y-as

$\,M_{y}=0$, aangezien F_x en F_z beiden 0 zijn.

Buigmoment rond z-as

$\,M_{z}=(-L_{BC})\times F_{x}-(L_{AB}-x)\times F_{y}=-1\times 0-F\times (L_{AB}-x)=-F\times (L_{AB}-x)$

Het buigmoment bereikt een maximum voor x=0 (punt A) en is gelijk aan 0 voor x=5 (punt B)

Balkdeel BC (lokaal assenkruis met lokale x-as van B naar C, lokale y-as van C naar D en lokale z-as volgens x-as van het globaal assenkruis). Enkel de snedekrachten verchillend van 0 worden uitgewerkt:

Evenwicht volgens lokale x-as (= negatieve globale y-as)

$\,N=-F_{y}=-10kN$

Buigmoment rond lokale z-as (= globale x-as)

$\,M_{z-lokaal}=M_{x}=(-L_{CD})\times F_{y}-(-L_{BC})\times F_{z}=(-2)\times 10-(-1)\times 0=-20kNm$

Balkdeel CD (lokaal assenkruis met lokale x-as van C naar D, lokale y-as is gelijk aan globale y-as en lokale z-as volgens x-as van het globaal assenkruis). Enkel de snedekrachten verchillend van 0 worden uitgewerkt:

Evenwicht volgens lokale y-as (=globale y-as)

$\,T_{y}=F_{y}=10kN$

Buigmoment rond lokale z-as (= globale x-as)

$\,M_{z-lokaal}=M_{x}=(-L_{CD}-z)\times F_{y}-(0)\times F_{z}=-(L_{CD}+z)\times F_{y}$

Het buigmoment bereikt een maximum voor z=0 (punt C) en is gelijk aan 0 voor z=-2 (punt D)

We kunnen op basis van de NTM-diagramma's vaststellen dat:

• De normaalkracht N over de hele lengte van balkdeel BC gelijk is aan een drukkracht van $\,-F_{y}=-10kN$.
• De dwarskracht T over de hele lengte van de balkdelen AB en CD gelijk zijn aan $\,F_{y}=10kN$.
• Het buigmoment M lineair varieert over de lengte van de balkdelen AB en CD met een maximum van -50 kNm in punt A.
• Het wringmoment $M_{t}$ over de hele lengte van balkdeel AB gelijk is aan $\,L_{CD}\times F_{y}=20kN$.

Voorbeeld 4 - verdeelde belastingen

Verdeelde belastingen

In alle voorgaande voorbeelden werden enkel puntlasten beschouwd, dit zijn krachten die aangrijpen in een punt. Deze puntlast kan zowel een kracht als een moment zijn.

Verdeelde lasten zijn belastingen die niet in 1 punt aangrijpen maar die aangrijpen over een zekere lengte. Deze belastingen worden met kleine letters aangeduid en kunnen een verdeelde kracht of een verdeeld moment zijn. Verdeelde lasten kunnen constant, lineair of een totaal willekeurige van vorm zijn. Ze worden meestal uitgedrukt als functie van een ruimtelijke veranderlijke.

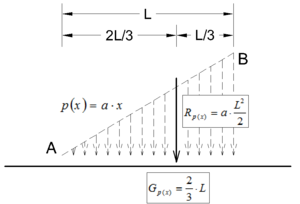
Voor het berekenen van de uitwendige krachten via de evenwichtsvergelijkingen, mogen we elke verdeelde kracht vervangen door de resulterende kracht R aangrijpend in het zwaartepunt G van de verdeelde kracht. Deze resultante door het zwaartepunt is immers statisch gelijkwaardig. Voor het berekenen van de resultante en het aangrijpingspunt kunnen we gebruikmaken van volgende formules:

• berekenen van de grootte van de resultante van een verdeelde kracht of moment:

$\,R_{p(x)}=\int _{A}^{B}p(x)dx$

• berekenen van het aangrijpingspunt van de resultante (zwaartepunt van de functie):

$G_{p(x)}={\frac {\int _{A}^{B}xp(x)\;dx}{\int _{A}^{B}p(x)\;dx}}$

• Tabel met veel voorkomende gevallen: constante en lineaire verdeelde last:

Benaming	Uitdrukking	Resultante $R_{p(x)}$		Aangrijpingspunt $G_{p(x)}$		Grafische voorstelling
		Formule	Resultaat	Formule	Resultaat
CONSTANTE verdeelde kracht van A tot B	p(x)=a	$R_{p(x)}=\int _{A}^{B}adx$	$\,a.L_{AB}$	$G_{p(x)}={\frac {\int _{A}^{B}x.a\;dx}{\int _{A}^{B}a\;dx}}$	$\,L_{AB}/2$
LINEAIR variërende kracht van A tot B	p(x)=a.x	$R_{p(x)}=\int _{A}^{B}a.xdx$	$\,a.L_{AB}^{2}/2$	$G_{p(x)}={\frac {\int _{A}^{B}a.x^{2}\ dx}{\int _{A}^{B}a.x\;dx}}$	$\,2.L_{AB}/3$

Opgave

Onderstaande balk CD is opgelegd in punten A en B. Bereken de snedekrachten en bepaal de NTM-diagramma's. De belastingen hebben volgende waardes:

Type	Aanduiding	Grootte	Aangrijpingspunt	Aanvullende info
Moment	M	8 kNm	punt C
Kracht	P	5 kN	punt E
Verdeeld moment	m1(x)	m1(x)=1 kNm/m	van punt F tot punt G	constant op 1 kNm/m
Verdeelde kracht	p1(x)	p1(x)=2x/3 kN/m	van punt K tot punt L	lineair variërend van p1(K)=0 kN/m tot p1(L)= 2kN/m
Verdeelde kracht	p2(x)	p2(x)=2 kN/m	van punt B tot punt D	constant op 2 kN/m

Stap 1: Bepaling van de uitwendige krachten - vrijmaken

We bepalen eerst de uitwendige krachten.

• stap 1a: Referentie-assenkruis
  

We leggen de de x-as volgens de aslijn van de bbalk van C naar D, met de y-as vertikaal naar beneden gericht.

• stap 1b: Opzoeken en aanduiden van alle uitwendige krachten, inclusief de verbindingskrachten / reactiekrachten
  

Naast de 5 uitwendige krachten M, P, m1, p1 en p2 hebben we ook nog verbindingskrachten in punt A en punt B.

Punt A
In punt A hebben we een roloplegging, deze oplegging kan enkel krachten loodrecht op de oplegging opnemen. We duiden deze kracht aan als $\,R_{Ay}$

Punt B
In punt B hebben we te maken met gewone oplegging die een horizontale en een vertikale kracht kan opnemen. We duiden de krachten aan als $\,R_{By}$ (vertikaal) en $\,R_{Bx}$ (horizontaal).

• stap 1c: Schematische voorstelling - vrijmaken
  

We duiden alle externe krachten aan op een schematische voorstelling zoals hieronder.

• stap 1d: Berekenen uitwendige krachten
  

Door de evenwichtvergelijkingen van de statica (2.1.2) toe te passen , kunnen we alle externe krachten bepalen.

Horizontaal evenwicht:

$\,-R_{Bx}=0\,=>R_{Bx}=0kN$

Vertikaal evenwicht:

$\,P-R_{Ay}+\int _{K}^{L}p_{1}(x)dx-R_{By}+\int _{B}^{D}p_{2}(x)dx=0$

met $\int _{K}^{L}p_{1}(x)dx=2/3[x^{2}/2]_{K}^{L}=2/3\times [3^{2}/2-0^{2}/2]=3kN$ = totale kracht p1 van punt K tot L = resultante p1;

$\,\int _{B}^{D}p_{2}(x)dx=2[x]_{B}^{D}=2\times [3-0]=6kN$ = totale kracht p1 van punt B tot D = resultante p2;

geeft dit:

$\,R_{Ay}+R_{By}=5+3+6=14kN$

Uit het momentenevenwicht halen we dat $\,R_{Ay}=4kN$, zodat $\,R_{By}=10kN$

Momentenevenwicht rond punt B

$\,M+(-L_{EB}).P+(-L_{AB}).(-R_{Ay})+\int _{F}^{G}m_{1}(x)dx+(-L_{G_{p1}B}).\int _{K}^{L}p_{1}(x)dx+(L_{G_{p2}B}).\int _{B}^{D}p_{2}(x)dx=0$

met $\,(-L_{EB}).P=-9\times 5=-45kNm$ = moment geleverd door de kracht P tov B.

$\int _{F}^{G}m_{1}(x)dx=[x]_{F}^{G}=[2-0]=2kNm$ = totaal moment m1 van punt F tot G = resultante m1;

$\,-L_{G_{p1}B}=-(L_{G_{p1}L}+L_{LB})=-(1/3\times 3+1)=-2m$ = hefboomsarm van resultante van p1 tov van B.

$\,L_{G_{p2}B}=1/2\times 3=1,5m$ = hefboomsarm van resultante van p2 tov van B.

geeft dit:

$\,8-45+8\times R_{Ay}+2-2\times 3+1,5\times 6=0\,=>8\times R_{Ay}=32\,=>R_{Ay}=4kN$

Stap 2: Bepaling van de snedekrachten - opstellen NTM-diagramma's

Nu alle uitwendige krachten zijn berekend, kunnen we overgaan tot het berekenen van de snedekrachten. Voor het berekenen van de snedekrachten moeten we gebruik maken van de werkelijk inwerkende krachten, en mogen we de verdeelde lasten niet vervangen door hun resultantes. We gebruiken een x-as met oorsprong in het punt C. We bouwen de formules op van punt C naar punt D en nemen een daartoe een snede die we laten "bewegen" over de x-as van C naar D. De krachten op dit deel zijn statisch gelijkwaardig aan de krachten die inwerken op het linkerdeel.

Snedekrachten tussen punt C en E
Er is op dit deel enkel het moment M=8knM in het punt C

• $\,T_{y}=0kN$
• $\,M_{z}=M=8kNm$

Snedekrachten tussen punt E en A
Er op dit deel enkel het moment M=8knM in het punt C en een kracht P=5kN in het punt E (Voor E geldt x=1m, voor A x=2m)

• $\,T_{y}=-P=-5kN$
• $\,M_{z}=M-L_{EX}.P=(8-5(x-1))=(13-5x)kNm$

voor punten E en A geldt: $M_{z}(E)=(13-5\times 1)=8kNm$ en $M_{z}(A)=(13-5\times 2)=3kNm$

Snedekrachten tussen punt A en F
We hebben een bijkomende kracht RAy=4kN in het punt A (voor A geldt x=2m, voor F x=3m)

• $\,T_{y}=-P+R_{Ay}=-5+4=-1kN$
• $\,M_{z}=M-L_{EX}.P+L_{AX}.R_{Ay}=(8-5(x-1)+4(x-2))=(5-x)kNm$

voor punten A en F geldt:$M_{z}(A)=(5-2)=3kNm$ en $M_{z}(F)=(5-3)=2kNm$

Snedekrachten tussen punt F en G
We hebben een bijkomende kracht m1 van het punt F tot G (voor F geldt x=3m, voor G x=5m)

• $\,T_{y}=-P+R_{Ay}=-5+4=-1kN$
• $\,M_{z}=M-L_{EX}.P+L_{AX}.R_{Ay}+\int _{F}^{x}m_{1}(x)dx=(8-5(x-1)+4(x-2)+(x-3))=2kNm$

voor punten F en G geldt:$M_{z}(F)=2kNm$ en $M_{z}(G)=2kNm$

Snedekrachten tussen punt G en K
We hebben geen bijkomende krachten van het punt G tot K (voor G geldt x=5m, voor K x=6m)

• $\,T_{y}=-P+R_{Ay}=-5+4=-1kN$
• $\,M_{z}=M-L_{EX}.P+L_{AX}.R_{Ay}+\int _{F}^{G}m_{1}(x)dx=(8-5(x-1)+4(x-2)+1\times 2)=(7-x)kNm$

voor punten B en F geldt:$M_{z}(G)=(7-5)=2kNm$ en $M_{z}(K)=(7-6)=1kNm$

Snedekrachten tussen punt K en L
We hebben een bijkomende kracht p1 van het punt K tot L (voor K geldt x=6m, voor L x=9m)

• $\,T_{y}=-P+R_{Ay}-\int _{K}^{x}p_{1}(x)dx=-5+4-{\frac {2}{3}}.{\frac {(x-6)^{2}}{2}}=(-1-{\frac {x^{2}-12x+36}{3}})=(-13+4x-{\frac {1}{3}}x^{2})kN$

voor punten K en L geldt:$T_{y}(K)=(-13+24-12)=-1kNm$ en $T_{y}(L)=(-13+36-27)=-4kNm$

• $\,M_{z}=M-L_{EX}.P+L_{AX}.R_{Ay}+\int _{F}^{G}m_{1}(x)dx-\int _{K}^{x}p_{1}(x)dx.{\frac {1}{3}}L_{KX}=8-5(x-1)+4(x-2)+1\times 2-{\frac {2}{3}}.{\frac {(x-6)^{2}}{2}}.{\frac {1}{3}}(x-6)=(31-13x+2x^{2}-{\frac {1}{9}}x^{3})kNm$

voor punten K en L geldt:$M_{z}(K)=(31-78+72-24)=1kNm$ en $M_{z}(L)=(31-117+162-81)=-5kNm$

Snedekrachten tussen punt L en B
We hebben geen bijkomende van het punt L tot B (voor L geldt x=9m, voor B x=10m)

• $\,T_{y}=-P+R_{Ay}-\int _{K}^{L}p_{1}(x)dx=-5+4-{\frac {2}{3}}.{\frac {(9-6)^{2}}{2}}=-4kN$

voor punten K en L geldt:$T_{y}(L)=-4kNm$ en $T_{y}(B)=-4kNm$

• $\,M_{z}=M-L_{EX}.P+L_{AX}.R_{Ay}+\int _{F}^{G}m_{1}(x)dx-\int _{K}^{L}p_{1}(x)dx.(L_{LX}+1)=8-5(x-1)+4(x-2)+1\times 2-{\frac {2}{3}}.{\frac {(9-6)^{2}}{2}}.(x-9+1)=(31-4x)kNm$

voor punten L en B geldt:$M_{z}(L)=(31-36)=-5kNm$ en $M_{z}(B)=(31-40)=-9kNm$

Snedekrachten tussen punt B en D
We hebben een bijkomende kracht RBy in B en een bijkomende kracht p2 van het punt B tot D (voor B geldt x=10m, voor D x=13m)

• $\,T_{y}=-P+R_{Ay}-\int _{K}^{L}p_{1}(x)dx+R_{By}-\int _{B}^{x}p_{2}(x)dx=-5+4-{\frac {2}{3}}.{\frac {(9-6)^{2}}{2}}+10-2(x-10)=(26-2x)kN$

voor punten K en L geldt:$T_{y}(B)=6kNm$ en $T_{y}(L)=26-26=0kNm$

• $\,M_{z}=M-L_{EX}.P+L_{AX}.R_{Ay}+\int _{F}^{G}m_{1}(x)dx-\int _{K}^{L}p_{1}(x)dx.(L_{LX}+1)+L_{BX}.R_{By}-\int _{B}^{x}p_{2}(x)dx.{\frac {1}{2}}L_{BX}=31-4x+10(x-10)-2(x-10).{\frac {x-10}{2}}=(-169+26x-x^{2})kNm$

voor punten B en D geldt:$M_{z}(B)=(-169+260-100)=-9kNm$ en $M_{z}(D)=(-169+338-169)=0kNm$

Relaties tussen belastingen en snedekrachten

Algemene relaties

Bij voorbeeld 4 - verdeelde belasting bleek dat de formules voor het opstellen van de snedekrachten al snel behoorlijk ingewikkeld kunnen worden.

Het opzoeken van dwarskrachten en buigmomenten in dergelijke balken kan sterk vereenvoudigd worden doordat er verbanden bestaan tussen de belastingen, de dwarskrachten en de buigmomenten. Om deze verbanden te bepalen beschouwen een elementair balkdeeltje met lengte dx, waarop diverse krachten inwerken zoals op de figuur hieronder.

De snede krachten op punt x zijn gelijk aan N(x), T(x) en M(x). In punt (x+dx) zijn deze gewijzigd in N(x+dx), T(x+dx), M(x+dx). Deze wijzigingen zijn het gevolg van de verdeelde lasten n(x), p(x) en m(x), die constant worden verondersteld over de elementaire lengte dx.

We kunnen nu het statisch evenwicht uitschrijven voor het elementair balkdeel dx:

• Horizontaal evenwicht:

$\!-N(x)+n(x).dx+N(x+dx)=0=>-N(x)+N(x+dx)=-n(x).dx$

We kunnen N(x+dx) uitschrijven in een Taylorontwikkeling rond het punt x:

$N(x+dx)=\sum _{n=0}^{\infty }{\frac {d^{n}N(x)}{dx^{n}}}{\frac {(x+dx-x)^{n}}{n!}}=N(x)+{\frac {dN(x)}{dx}}.dx+{\frac {d^{2}N(x)}{dx^{2}}}{\frac {(dx)^{2}}{2!}}+...$

Indien we de hogere termen van de reeksontwikkeling verwaarlozen (=lineaire benadering), krijgen we volgend verband:

$\,-n(x)={\frac {dN(x)}{dx}}$

• Vertikaal evenwicht:

$\!-T(x)+p(x).dx+T(x+dx)=0=>-T(x)+T(x+dx)=-p(x).dx$

We kunnen T(x+dx) uitschrijven in een Taylorontwikkeling rond het punt x:

$T(x+dx)=\sum _{n=0}^{\infty }{\frac {d^{n}T(x)}{dx^{n}}}{\frac {(x+dx-x)^{n}}{n!}}=T(x)+{\frac {dT(x)}{dx}}.dx+{\frac {d^{2}T(x)}{dx^{2}}}{\frac {(dx)^{2}}{2!}}+...$

Indien we de hogere termen van de reeksontwikkeling verwaarlozen (=lineaire benadering), krijgen we volgend verband:

$\,-p(x)={\frac {dT(x)}{dx}}$

• Uit het momentenevenwicht rond het zwaartepunt van de snede (x+dx) volgt:

$\!M(x)+T(x).dx-p(x).dx^{2}/2+m(x).dx-M(x+dx)=0=>M(x+dx)=M(x)+T(x).dx-p(x).dx^{2}/2+m(x).dx$

We kunnen M(x+dx) uitschrijven in een Taylorontwikkeling rond het punt x:

$M(x+dx)=\sum _{n=0}^{\infty }{\frac {d^{n}M(x)}{dx^{n}}}{\frac {(x+dx-x)^{n}}{n!}}=M(x)+{\frac {dM(x)}{dx}}.dx+{\frac {d^{2}M(x)}{dx^{2}}}{\frac {(dx)^{2}}{2!}}+...$

Indien we de hogere termen van de reeksontwikkeling (=lineaire benadering) en de tweede grootteorde in p(x) verwaarlozen, krijgen we volgend verband:

$\,T(x)+m(x)={\frac {dM(x)}{dx}}$

Indien er geen verdeelde uitwendige momenten m(x) aanwezig zijn, wordt dit herleid tot:

$\,T(x)={\frac {dM(x)}{dx}}$

opgelet:De tekens in bovenstaande uitdrukkingen worden bepaald door de keuze van het assenkruis en van de positieve zin van snedekrachten.

Uit de bovenstaande relaties tussen krachten volgen enkele interessante besluiten:

• In een onbelast stuk van de balk (p(x)=0) is de dwarskracht constant. Als p(x) een constante is varieert de dwarskracht lineair, als p(x) lineair is varieert de dwarskracht parabolisch, enzovoort.
• Als er geen verdeelde uitwendige momenten m(x) inwerken, geldt dat:
  • Het buigmoment bereikt zijn extreme maximale of minimale waarden in de punten waar de dwarskracht gelijk is aan 0.
  • Bij een positieve waarde van de dwarskracht, stijgt het buigmoment; bij een negatieve dwarskracht daalt het buigmoment.
  • Zolang de dwarskracht T(x) constant is, blijft de helling van de buigmomentenlijn dezelfde, als T(x) lineair is varieert de buigmomentenlijn parabolisch, enzovoort.

We bekijken enkele veel voorkomende vormen van belastingen en bijhorende NTM-diagramma's in enkele voorbeelden.

Voorbeeld 1: Tweezijdig opgelegde balk met gelijkmatig verdeelde last

Een balk opgelegd in A en B wordt belast door een gelijkmatig verdeelde last p.

• Uitwendige krachten:

Vertikaal evenwicht

$V_{A}+V_{B}=p.L$

Rotatie-evenwicht rond punt B

$V_{A}.L=p.L^{2}/2$

$=>V_{A}=V_{B}={\frac {p.L}{2}}$

• Snedekrachten:

$T(x)={\frac {p.L}{2}}-p.x=p({\frac {L}{2}}-x)$

$M(x)={\frac {p.L}{2}}.x-p.x.{\frac {x}{2}}={\frac {px}{2}}(L-x)$

• Uiterste waarden dwarskracht:

$T_{A}={\frac {p.L}{2}}\,\,\,;\,\,\,T_{B}=-{\frac {p.L}{2}}$

• de dwarskracht is gelijk aan nul voor x = L/2. Hier bereikt het buigmoment zijn maximale waarde:

$M_{max}=M_{\frac {L}{2}}={\frac {p}{2}}.{\frac {L}{2}}(L-{\frac {L}{2}})={\frac {p.L^{2}}{8}}$

• Men kan eenvoudig vaststellen dat de dwarskrachtenfunctie de afgeleide is van de buigmomentenfunctie:

${\frac {dM(x)}{dx}}={\frac {d}{dx}}({\frac {pLx}{2}}-{\frac {px^{2}}{2}})={\frac {pL}{2}}-{\frac {2px}{2}}=p({\frac {L}{2}}-x)=T(x)$

Voorbeeld 2: Tweezijdig opgelegde balk met willekeurige puntlast

Een balk opgelegd in A en B wordt belast door een puntlast P aangrijpend in het punt C op afstanden a en b van de steunpunten.

• Uitwendige krachten:

Vertikaal evenwicht

$V_{A}+V_{B}=P$

Rotatie-evenwicht rond punt B

$V_{A}.L=P.b$

$=>V_{A}={\frac {P.b}{L}}$

$=>V_{B}=P-V_{A}=P{\frac {L}{L}}-{\frac {P.b}{L}}={\frac {P}{L}}(L-b)={\frac {P.a}{L}}$

• Snedekrachten: er moet onderscheid gemaakt worden tussen de gebieden AC en CB. Als we een snede maken links van C werkt enkel de kracht $V_{A}$ op het linkerdeel van de balk. Bij een snede rechts van het punt C, werken de krachten $V_{A}$ en P.

in het balkdeel AC:	$T(x)=V_{A}={\frac {P.b}{L}}$
	$M(x)={\frac {P.b}{L}}.x$
in het balkdeel CB:	$T(x)=V_{A}-P={\frac {P.b}{L}}-P={\frac {P.(b-L)}{L}}=-{\frac {P.a}{L}}$
	$M(x)={\frac {P.b}{L}}.x-P(x-a)={\frac {P.a}{L}}(L-x)$

• De dwarskracht gaat over van positief naar negatief voor x = a. Hier bereikt het buigmoment zijn maximale waarde:

$M_{max}=M_{a}={\frac {Pab}{L}}$

• Als de last P aangrijpt in het midden van de balk geldt a=b=L/2. De maximale waarde van het buigmoment is in dit geval:

$M_{max}=M_{\frac {L}{2}}={\frac {PL}{4}}$

• Men kan vaststellen dat de dwarskrachtenfunctie de afgeleide is van de buigmomentenfunctie in zowel balkdeel AC als CB
• De buigmomentenlijn heeft een discontinue afgeleide in punt C: de buigmomentenlijn vertoont daar een knik. Deze knik komt steeds voor als de dwarskrachtenlijn een sprong vertoont. Dit is steeds het geval op de plaatsen waar een geconcentreerde kracht (puntlast) aangrijpt. De knik in de momentelijn is enkel een extreme waarde, als de dwarskracht in dat punt van teken verandert.

Voorbeeld 3: Tweezijdig opgelegde balk met willekeurig moment

Een balk opgelegd in A en B wordt belast door een moment M aangrijpend in het punt C op afstanden a en b van de steunpunten.

• Uitwendige krachten:

Vertikaal evenwicht

$V_{A}+V_{B}=0$

Rotatie-evenwicht rond punt B

$V_{A}.L+M=0$

$=>V_{A}=-{\frac {M}{L}}$

$=>V_{B}={\frac {M}{L}}$

• Snedekrachten: Voor het buigmoment moet er onderscheid gemaakt worden tussen de gebieden AC en CB. Als we een snede maken links van C werkt enkel de kracht VA op het linkerdeel van de balk. Bij een snede rechts van het punt C, werken de krachten VA en M. De dwarskrachten zijn constant over de ganse lengte L.

over de ganse balk:	$T(x)=V_{A}=-{\frac {M}{L}}$
in het balkdeel AC:	$M(x)=V_{A}.x=-{\frac {M}{L}}.x$
in het balkdeel CB:	$M(x)=V_{A}.x+M={\frac {M}{L}}(L-x)$

• De helling van de momentenlijn is dezelfde in de zone AC en de zone CB. Over de ganse balk is de afgeleide van de momentenlijn gelijk aan de dwarskrachtenlijn.
• De momentenlijn maakt een sprong in C. Deze sprong is het gevolg van het moment dat inwerkt in het punt C.

Oefeningen N T M - diagramma's

Oefening 2

---

<< Terug naar Evenwichtsvergelijkingen - Inwendige en uitwendige Krachten / Verder naar Basisbegrippen - Deel 1 >>