Klassieke Mechanica/Voorwerpendynamica

Het massacentrum

Bepaling van het massacentrum

In het vorige hoofdstuk werd de beweging bestudeerd van een puntmassa. Een puntmassa kan niet roteren omdat ze geen richting heeft. Reële voorwerpen zullen eerst beschouwd worden als een verzameling van puntmassa's, waarop men de conclusies uit het vorige hoofdstuk kan toepassen. Door te sommeren over alle puntmassa's, kan men dan specifieke wetten voor de rotatie afleiden.

In eerste instantie kan men zich de vraag stellen of er bij een voorwerp een punt is dat beweegt alsof alle uitwendige krachten daarop werken. Men onderstelt hiervoor een verzameling van puntmassa's m_i met posities ${\vec {r_{i}}}$ t.o.v. een vast punt. Op elk punt werken een aantal uitwendige krachten met resultante ${\vec {F_{i}^{ext}}}$ en inwendige krachten met resultante ${\vec {F_{i}^{int}}}$. Volgens de tweede wet van Newton kan men dan schrijven:

${\vec {F_{i}^{ext}}}+{\vec {F_{i}^{int}}}=m_{i}{\vec {a_{i}}}$

Wanneer men deze vergelijkingen lid aan lid optelt voor alle punten, dan verdwijnen de inwendige krachten uit deze som. Er blijft dus:

$\sum {\vec {F_{i}^{ext}}}=\sum {m_{i}{\vec {a_{i}}}}$      (1)

Stelt men $m=\sum {m_{i}}$, dan kan men zoeken naar een punt met coördinaat r_C zodat geldt:

$m{\vec {r_{C}}}=\sum {m_{i}{\vec {r_{i}}}}$

Een oplossing hiervoor is:

${\vec {r_{C}}}={\frac {\sum {m_{i}{\vec {r_{i}}}}}{m}}$      (2)

Men noemt dit punt het massacentrum van het systeem. Er geldt dan ook:

$m{\vec {v_{C}}}=\sum {m_{i}{\vec {v_{i}}}}$

$m{\vec {a_{C}}}=\sum {m_{i}{\vec {a_{i}}}}$

Wanneer men dit invult in de vergelijking (1), dan krijgt men:

$\sum {\vec {F_{i}^{ext}}}=m{\vec {a_{C}}}$

Of in woorden: het massacentrum beweegt alsof alle uitwendige krachten erop aangrijpen. Alles wat in vorig hoofdstuk gezegd werd over de beweging van een puntmassa, geldt voor de beweging van het massacentrum (anders had men waarschijnlijk niet zo veel aandacht besteed aan de beweging van een puntmassa).

Deze afleiding geldt zowel voor vervormbare als onvervormbare (of starre) systemen. Bij onvervormbare systemen zal het massacentrum een vaste plaats hebben in het voorwerp, bij vervormbare zal het zich binnen het systeem kunnen verplaatsen.

Men kan de coördinaten van het massacentrum uitrekenen door de uitdrukking (2) te projecteren op bv. de assen van een cartesisch assenkruis:

$x_{C}={\frac {\sum {m_{i}x_{i}}}{m}}\quad y_{C}={\frac {\sum {m_{i}y_{i}}}{m}}\quad z_{C}={\frac {\sum {m_{i}z_{i}}}{m}}$

Indien men een voorwerp beschouwt als opgebouwd uit een continue massaverdeling, dan moet de som vervangen worden door een integraal:

$x_{C}={\frac {\int {x.dm}}{\int {dm}}}\quad y_{C}={\frac {\int {y.dm}}{\int {dm}}}\quad z_{C}={\frac {\int {z.dm}}{\int {dm}}}$

Men ziet dat deze formules overeenkomen met de formules van het zwaartepunt voor zover de aantrekkingskracht van de aarde door evenwijdige krachten kan voorgesteld worden.

Eigenschappen van het massacentrum

1. Men kan zich bij de bepaling van het massacentrum ook laten leiden door het feit dat als het systeem een symmetrievlak of een symmetrieas heeft, het massacentrum dan in dat symmetrievlak of op die symmetrieas moet liggen.

Onderstelt men bv. dat het zx-vlak een symmetrievlak is dan betekent dit dat er voor elk punt met massa m_i en coördinaat y_i er ook een punt met massa m_j = m_i en coördinaat y_j = -y_i moet zijn. Bij sommeren over alle massa's vallen die tegen elkaar weg en eindigt men met een y_C=0, m.a.w. in het xz-vlak.

Op analoge manier kan men aantonen dat bij aanwezigheid van een symmetrieas het massacentrum op die symmetrieas moet liggen. Zij bv. de z-as een symmetrieas. Dan moet er voor elk punt met massa m_i en coördinaat x_i en y_i ook een punt zijn met massa m_j = m_i en coördinaat x_j = -x_i en y_j = -y_i. Bij sommeren over alle massa's zal men dus komen op een x_C=0 en y_C=0 d.i. op de z-as.

2. Het massacentrum wordt bepaald via een som (of integraal). Men kan die som opdelen in deelsommen. Dit betekent dat men een complex systeem eerst kan opsplitsen in eenvoudiger onderdelen waarvan het massacentrum gemakkelijk kan bepaald worden en dan die onderdelen kan combineren voor het massacentrum van het geheel. Hierbij beschouwt men de totale massa van elk onderdeel als geplaatst in het massacentrum van dat onderdeel. Voor een voorbeeld: zie bepaling van het zwaartepunt in het hoofdstuk over equivalente vectorsystemen.

3. Het massacentrum van een systeem hoeft niet noodzakelijk een materieel punt van dat systeem te zijn. Bij een holle bol zal het massacentrum samenvallen met het centrum van de bol maar daar is er geen massa aanwezig.

4. De aangrijpingspunten van de uitwendige krachten hebben dus geen belang voor de beweging van het massacentrum. Zij hebben nochtans wel belang voor de rotatie van het voorwerp of, meer algemeen, de beweging t.o.v. het massacentrum. Men zal verder de algemene beweging van een voorwerp splitsen in een beweging van het massacentrum, de translatiecomponent, en een beweging t.o.v. het massacentrum. Als het voorwerp roteert dan zal de verplaatsing van het aangrijpingspunt van de uitwendige krachten anders zijn dan indien het niet roteert. Men zal verder aantonen dat de som van de uitwendige krachten met de verplaatsing van het massacentrum bepalend is voor de kinetische energie van de translatie en de verplaatsing t.o.v. het massacentrum voor een tweede term. Bij een onvervormbaar voorwerp zal die de kinetische energie van de rotatie voorstellen.

5. Massacentrum en zwaartepunt worden bepaald met dezelfde formules voor zover men mag onderstellen dat de aantrekkingskrachten van de aarde op elk deeltje van een voorwerp evenwijdige krachten zijn. Als deze onderstelling niet meer klopt, zal het massacentrum niet samenvallen met het zwaartepunt.

Beweging t.o.v. het massacentrum

Men kan de positie van de samenstellende massa's ook bepalen t.o.v. het massacentrum zelf. Deze positievectoren zullen aangegeven worden met een accent. Wanneer men vertrekt van het massacentrum zelf als referentiepunt dan moet gelden :${\vec {r_{C}}}=0$. Men heeft dus ook:

$\sum {m_{i}{\vec {r_{i}^{'}}}}=0\quad \sum {m_{i}{\vec {v_{i}^{'}}}}=0\quad \sum {m_{i}{\vec {a_{i}^{'}}}}=0$

Deze betrekkingen zullen voortdurend terugkomen bij de studie van de rotatiebeweging en ervoor zorgen dat de formules sterk vereenvoudigen als men de beweging van een voorwerp beschrijft als een beweging van het massacentrum + een beweging t.o.v. het massacentrum.

Massacentrum en behoud van impuls

Wanneer er geen uitwendige krachten werken op een systeem, dan moet de totale hoeveelheid van beweging constant blijven. Als men de uitdrukking hiervoor vergelijkt met de uidrukking voor de snelheid van het massacentrum hierboven, dan blijkt dat ook de snelheid van het massacentrum dan constant is.

$\sum {m_{i}{\vec {v_{i}}}}={\vec {C}}\Leftrightarrow m{\vec {v_{C}}}={\vec {C}}$

Impulsmoment van een vrij bewegend voorwerp

Men kan de positie van een puntmassa opschrijven als de positie van het massacentrum + de relatieve positie van die massa t.o.v. het massacentrum. Dus:

${\vec {r}}_{i}={\vec {r}}_{C}+{\vec {r'}}_{i}$

Ook voor de snelheden kan men schrijven:

${\vec {v}}_{i}={\vec {v}}_{C}+{\vec {v'}}_{i}$

Wanner men dit invoert in de formule voor het impulsmoment bekomt men:

${\vec {L}}=\sum ({\vec {r}}_{C}+{\vec {r'}}_{i})\times m_{i}({\vec {v}}_{C}+{\vec {v'}}_{i})$

$={\vec {r}}_{C}\times (\sum m_{i}){\vec {v}}_{C}\,+\,{\vec {r}}_{C}\times (\sum m_{i}{\vec {v'}}_{i})\,+\,(\sum _{i}m_{i}{\vec {r'}}_{i})\times {\vec {v}}_{C}\,+\,\sum ({\vec {r'}}_{i}\times m_{i}{\vec {v'}}_{i})$

Daar $\sum m_{i}{\vec {r'}}_{i}=0\,en\,\sum m_{i}{\vec {v'}}_{i}=0$ zijn de tweede en de derde term = 0. Er blijft:

${\vec {L}}={\vec {r}}_{C}\times m{\vec {v}}_{C}\,+\,\sum ({\vec {r'}}_{i}\times m_{i}{\vec {v'}}_{i})$

In sommige landen is deze formule bekend als de eerste wet van König. De eerste term wordt ook wel het baanimpulsmoment genoemd en soms aangeduid als J. De tweede term is het impulsmoment t.o.v. het massacentrum. Bij een roterend onvervormbaar voorwerp zal dit ook wel met S van spin aangeduid worden. De formule wordt dan:

${\vec {L}}={\vec {J}}+{\vec {S}}$

Bij het berekenen van het impulsmoment t.o.v. het massacentrum mag men zowel met de absolute als met de relatieve snelheden rekenen. Gebruik van de absolute snelheden komt neer op het berekenen van het totale impulsmoment, baanimpulsmoment + spin, t.o.v. het massacentrum. Het baanimpulsmoment is dan ${\vec {r'}}_{C}\times m{\vec {v}}_{C}$ met r'_C de positie van het massacentrum t.o.v. het massacentrum. Die vector is natuurlijk nul en er blijft alleen een bijdrage van de relatieve snelheden.

Massacentrum en energie

Bij opsplitsen in een beweging van het massacentrum en een beweging t.o.v. het massacentrum vindt men voor de kinetische energie:

${\vec {v_{i}}}={\vec {v_{C}}}+{\vec {v_{i}^{'}}}$

$\sum {\frac {m_{i}.v_{i}^{2}}{2}}={\frac {(\sum {m_{i}})v_{C}^{2}}{2}}+\sum {\frac {m_{i}.v_{i}^{'2}}{2}}+(\sum {m_{i}{\vec {v_{i}^{'}}}})\cdot {\vec {v_{C}}}$

Hierin is de laatste term = 0 (zie hierboven), zodat er overblijft:

$E_{k}={\frac {mv_{C}^{2}}{2}}+\sum {\frac {m_{i}.v_{i}^{'2}}{2}}$

• De eerste term geeft de kinetische energie van het massacentrum alsof de hele massa daarin geconcentreerd is.
• De tweede term geeft de kinetische energie van de beweging t.o.v. het massacentrum.

Deze formule staat in de literatuur bekend als de (tweede) wet van König. Bemerk wel dat alleen bij een opsplitsen in beweging van het massacentrum en beweging t.o.v. het massacentrum de uitdrukking van de kinetische energie vereenvoudigt tot 2 termen i.p.v. 3.

König (1712 - 1757) publiceerde deze wetten in 1751 toen hij in Berlijn werkte. Voor meer over de figuur van König, zie John Samuel König en Samuel König

De arbeid van alle krachten van een systeem waarop zowel inwendige als uitwendige krachten werken, kan men berekenen door de verplaatsing van elk aangrijpingspunt samen te stellen uit een verplaatsing van het massacentrum en een verplaatsing t.o.v. het massacentrum:

$d{\vec {r_{i}}}=d{\vec {r_{C}}}+d{\vec {r_{i}^{'}}}$

Men bekomt dan:

$\sum {\vec {F_{i}^{ext}}}\cdot d{\vec {r_{i}}}+\sum {\vec {F_{i}^{int}}}\cdot d{\vec {r_{i}}}=(\sum {\vec {F_{i}^{ext}}})\cdot d{\vec {r_{c}}}+\sum {{\vec {F_{i}^{ext}}}\cdot d{\vec {r_{i}^{'}}}}+(\sum {\vec {F_{i}^{int}}})\cdot d{\vec {r_{c}}}+\sum {{\vec {F_{i}^{int}}}\cdot d{\vec {r_{i}^{'}}}}$

Omwille van de actie-reactiewet moet de som van de inwendige krachten = 0 zijn. De derde term valt dus weg. Vergelijkt men deze uitdrukking met de uitdrukking voor de kinetische energie, dan is het duidelijk dat:

• $(\sum {\vec {F_{i}^{ext}}})\cdot d{\vec {r_{c}}}={\frac {mv_{C}^{2}}{2}}$
• $\sum {{\vec {F_{i}^{ext}}}\cdot d{\vec {r_{i}^{'}}}}+\sum {{\vec {F_{i}^{int}}}\cdot d{\vec {r_{i}^{'}}}}=\sum {\frac {m_{i}.v_{i}^{'2}}{2}}$

Voor de berekening van de kinetische energie geassocieerd met het massacentrum moet men alleen rekening houden met de verplaatsing van het massacentrum, ongeacht het aangrijpingspunt van de krachten.

Voor de berekening van de kinetische energie van de beweging t.o.v. het massacentrum moet men rekening houden met de effectieve verplaatsing van de aangrijpingspunten t.o.v. het massacentrum. Als het voorwerp een onvervormbaar voorwerp is, dan kunnen de inwendige krachten geen netto arbeid leveren en valt de bijdrage van de arbeid van de inwendige krachten weg.

Rotatie rond as met vaste richting

Inleiding

Bij rotatie kan men een onderscheid maken tussen rotatie om een as met vaste richting en de algemene rotatie. De eerste beweging kan beschreven worden met vrij eenvoudige formules, die sterk parallel lopen met de formules voor de lineaire beweging. Het algemene geval speelt zich af in drie dimensies, doet beroep op vectoriële producten en matrixbewerkingen en is daardoor veel complexer.

Wanneer men met een fiets rechtdoor rijdt, eventueel over een vertragingsbult, valt de beweging van de wielen onder het eerste geval. De as beweegt wel, maar de richting ervan verandert niet. Wanneer men echter met een boog rond een putje in het fietspad rijdt, valt de beweging onder het algemene geval. De beweging van veel draaiende onderdelen in machines valt ook onder de eerste beschrijving.

Bij rotatie rond een as met vaste richting zijn de formules eendimensionaal. Men kan dus spreken van eendimensionale rotatie. Dikwijls wordt deze beweging ook vlakke beweging genoemd, omdat alle punten van het voorwerp blijven bewegen in een vlak loodrecht op de rotatieas. Meer algemeen is een vlakke beweging een beweging waarbij de baan van elk punt in een vlak blijft en banen van verschillende punten in een zelfde of evenwijdige vlakken liggen. Ook een driedimensionaal voorwerp kan dus een vlakke beweging uitvoeren.

We hebben het hier uitsluitend over onvervormbare of starre voorwerpen.

Nota: Misschien is het nuttig hier even te herhalen wat reeds in Kinematica gezegd werd. Er is een essentieel verschil tussen een cirkelbeweging en een rotatie. Bij een beweging op een cirkel gaat het over een punt, eventueel een punt van een voorwerp, dat een cirkelbaan volgt. Bij een rotatie gaat het over een voorwerp, waarvan de oriëntatie verandert. Waarschijnlijk staan de meeste elektrische motoren stil. Hun rotor, het draaiend deel ervan, blijft ter plaatse. Het enige verband is dat bij een roterend voorwerp elk punt van het voorwerp een cirkel beschrijft t.o.v. de rotatieas, in een vlak loodrecht op die as (of minstens een stukje van zo'n cirkel). Zie ook "Rotatie versus translatie" verderop

Grootheden

We zullen beginnen met het verduidelijken van een reeks termen. Wanneer een voorwerp kan draaien rond een as, men zijn positie vastleggen door een hoek θ gemeten vanuit een referentiepositie. Als het voorwerp draait, heeft het een hoeksnelheid ω. Als die snelheid verandert, is er sprake van een hoekversnelling α. Men krijgt dus de volgende parallel tussen lineaire beweging of translatie en rotatie:

	translatie	rotatie
positie	positievector ${\vec {r}}$	hoek θ eenheid: radialen
eerste afgeleide	snelheid ${\vec {v}}$ m/s	hoeksnelheid ω rad/s
tweede afgeleide	versnelling ${\vec {a}}$ m/s2	hoekversnelling α rad/s2

Daaruit volgen formules analoog aan de lineaire beweging. Voor een eenparige rotatie geldt: θ(t) = θ₀ + ω.t
Voor een eenparig versnelde rotatie: θ(t) = θ₀ + ω₀.t + α.t²/2

De hoeksnelheid ω wordt voorgesteld als een vector gericht langs de rotatieas. Bij rotatie rond een as met vaste richting zal ook α volgens deze as liggen. Er zijn dan maar 2 mogelijkheden voor de zin van beide. Volgens één richting zal men de waarden van ω en α als positief rekenen, volgens de andere als negatief. Zolang men geen vectoriële producten gebruikt, kan men vrij kiezen welke zin men positieve zin noemt.

Het moment van een kracht t.o.v. de as is gelijk aan het product van de component van de kracht in een vlak loodrecht op de as met de afstand van de as tot de drager van die component. In de meeste gevallen gaat het over krachten die werken in een vlak loodrecht op de rotatieas, zoals wanneer je op de pedalen van je fiets duwt, zodat de component hierboven in feite de volledige kracht is. Dan krijgen we dus het klassieke moment = kracht x krachtarm. Voor een uitgebreider bespreking van mogelijke manieren om een moment uit te rekenen zie het einde van Elementaire bewerkingen met vectoren in het eerste hoofdstuk.

In het algemeen kan men de beweging van een voorwerp (bv. een fietswiel) beschrijven als de beweging van een referentiepunt (bv. punt op de fietsas) en een rotatie van het voorwerp rond een as door dat referentiepunt. Het blijkt dat die rotatie onafhankelijk is van het referentiepunt, maar typisch voor het voorwerp. De formules voor het beschrijven van deze beweging worden sterk vereenvoudigd als men een as beschouwt die ofwel stilstaat ofwel door het massacentrum van het voorwerp gaat. In dat laatste geval zal men meestal de beweging moeten beschrijven als samengesteld uit twee bewegingen: een beweging van het massacentrum en een rotatie rond een as door het massacentrum. Voorbeelden vindt men hieronder.

Basiswet

Eenvoudigste geval

Nemen we een zeer eenvoudig voorbeeld van 1 massa m op een afstand r van een as. Die as wordt aan het draaien gebracht door een riem die over een schijf loopt. De riem trekt aan de schijf met kracht F op afstand d van de as. Volgens de wet van de hefbomen kan men stellen dat deze kracht zich zal laten voelen op de massa als een kracht F' volgens de formule F.d = F'.r . Dit is in feite een momentenvergelijking die zegt dat het moment van F t.o.v. de as hetzelfde moet zijn als het moment van F' t.o.v. de as. Anderzijds is de versnelling a van de massa te schrijven als r.α (r.alfa). De wet van Newton zegt nu: F' = ma . Vermenigvuldigen we beide leden met r dan bekomen we: r.F' = r.m.a . Gebruiken we nu de bovenstaande gelijkheden dan kunnen we dit schrijven als :

d.F = m.r².α

De grootheid m.r² heet het traagheidsmoment van m t.o.v. de as en wordt normaal voorgesteld als I (de I van "inertia"). Een gewoon voorwerp zal normaal beschouwd worden als opgebouwd uit meerdere puntmassa's of uit een continue massaverdeling. Het traagheidsmoment wordt dan gedefinieerd als:

traagheidsmoment t.o.v. een as:

$I_{as}=\sum m_{i}.r_{i}^{2}\quad \mathrm {of} \quad I_{as}=\int r^{2}dm$, met r = afstand van elk punt tot de as.

We kunnen de formule dus lezen als: het moment van de kracht t.o.v. de as moet gelijk zijn aan traagheidsmoment x hoekversnelling.

Voor een meer realistische situatie met een reëel voorwerp i.p.v. juist één massa, zal men dit voorwerp beschouwen als opgebouwd uit kleine massa's. We moeten dan de som nemen over al deze massa's en als er meerdere krachten zijn ook over de momenten van alle krachten. Dit levert dan de echte basisformule voor de rotatie (met M_asF het moment van F t.o.v. de as, I_as het traagheidsmoment t.o.v. dezelfde as):

 $\sum M_{as}{\vec {F}}_{i}=I_{as}.\alpha$

De som van de momenten van de krachten t.o.v. de as moet gelijk zijn aan het traagheidsmoment t.o.v. die as x hoekversnelling

Het bewijs hierboven is voor een stilstaande (vaste) as. De formule geldt ook voor een as door het massacentrum, zelfs als die beweegt. Het bewijs hiervoor kan men vinden bij de afleiding van de formules voor de algemene rotatie. In feite moet zich dus afvragen:

• Draait het voorwerp rond een vaste as? Dan kan men meestal volstaan met de momentenvergelijking zoals hierboven gegeven.
• Is er geen vaste rotatieas? Dan moet de beweging beschreven worden als een combinatie van een translatie van het massacentrum + een rotatie rond een as door het massacentrum. Men zal dan steeds zowel de wet van Newton als de momentenvergelijking moeten opschrijven.
  
  

---

Algemener bewijs
Men kan voor een meer algemeen bewijs vertrekken van de wet van Newton voor één massa. Men onderstelt de beweging in of evenwijdig aan het xy-vlak, zodat de momenten volgens de z-as liggen, en neemt het moment van beide leden t.o.v. de rotatieas:

$({\vec {r}}\times \sum {\vec {F}}_{i})_{z}=({\vec {r}}\times m{\vec {a}})_{z}$

Bij een roterend voorwerp kan de versnelling geschreven worden als de som van een normale en een tangentiële versnelling. Daar de normale versnelling door de as wijst, is haar moment t.o.v. de as = 0. Er blijft:

$({\vec {r}}\times \sum {\vec {F}}_{i})_{z}=mr^{2}\alpha$

Voor meerdere massa's past men deze formule toe op elke massa waarna men lid aan lid optelt:

$\sum _{j}({\vec {r}}_{j}\times \sum {\vec {F}}_{ij})_{z}=\sum m_{i}r_{i}^{2}\alpha$

De krachten kunnen nu uitwendige krachten zijn of inwendige, tussen twee massa's. Volgens de actie-reactiewet moeten de inwendige krachten in paren voorkomen die op dezelfde drager liggen, zodat de momenten tegen elkaar wegvallen. Er blijven dus alleen de uitwendige krachten over. Normaal formuleert men de som over de momenten van de krachten met één sommatie, waarbij sommige r_i dan dezelfde zullen zijn. Men krijgt dan:

$\sum ({\vec {r}}_{i}\times \sum {\vec {F}}_{i})_{z}=\sum m_{i}r_{i}^{2}\alpha =I_{as}\alpha$

of:

$\sum M_{as}F_{i}=I_{as}\alpha$

---

Enkele voorbeelden van traagheidsmomenten.
Voor een volle schijf is het traagheidsmoment t.o.v. een as door het centrum en loodrecht op de schijf: I_C = m.r²/2
Voor een dunne staaf met lengte L: I_C = m.L²/12
Voor een rechthoekige plaat met lengte L en breedte B:

• t.o.v. van een as loodrecht op de plaat: I₁ = m(L² + B²)/12
• t.o.v. van een as in het vlak van de plaat evenwijdig aan L: I₂ = m.B²/12

Voor schetsen van beide situaties: zie voorbeelden verder.

Voor tabellen van traagheidsmomenten van verschillende voorwerpen, zie traagheidsmoment.

Opmerking
Hierboven werd gesteld dat men de formules moet opschrijven t.o.v. een stilstaande as of t.o.v. een as door het massacentrum. Bij een as door het massacentrum moet men normaal ook de wet van Newton opschrijven, zodat men een stelsel vergelijkingen heeft (index C verwijst naar het massacentrum):

$\sum {\vec {F}}_{i}=m{\vec {a}}_{C}$

$\sum M_{as,C}{\vec {F}}_{i}=I_{as,C}.\alpha$

De verplaatsingsformule legt een verband tussen de linkerleden van deze formules. Hetzelfde verband moet dan ook gelden tussen de rechterleden. Als het in een bepaald geval zonder vaste as interessanter is om het moment uit te rekenen t.o.v. een ander punt dan het massacentrum, bv. P, dan kan men het rechterlid van de momentenvergelijking naar daar verplaatsen met de formule:

$\sum M_{as,P}{\vec {F}}_{i}=I_{as,C}.\alpha +({\overrightarrow {PC}}\times m{\vec {a}}_{C})_{z}$

Van het vectoriele product moet men natuurlijk alleen de component loodrecht op het bewegingsvlak gebruiken. Op deze manier heeft men feitelijk een grote vrijheid bij het opschrijven van de momentenvergelijking, tenminste voor ogenblikkelijke berekeningen.

Formule van Steiner

Als men een traagheidsmoment uitgerekend heeft t.o.v. een as en men heeft later het moment nodig t.o.v. een andere as, dan kan men zich afvragen of men volledig opnieuw moet beginnen met de berekening of men zijn vorig resultaat nog kan gebruiken. Een zekere Steiner vond dat dat laatste kan, op voorwaarde dat men vertrekt van een as door het massacentrum. Dan is het traagheidsmoment t.o.v. elke parallelle as door punt P gegeven door:

   $\displaystyle I_{P}=I_{c}+m.d^{2}$

met m de totale massa van het voorwerp en d de afstand tussen de 2 assen. Voorbeelden infra.

---

Bewijs

Formule van Steiner

Men onderstelt dat het traagheidsmoment gegeven is t.o.v. een z-as en gevraagd wordt t.o.v. een evenwijdige z'-as. Voor elke puntmassa in het systeem kan men dan schrijven dat, in een vlak loodrecht op de assen, de positie t.o.v. de z'-as gegeven is als:

${\vec {r'}}_{i}={\vec {d}}+{\vec {r}}_{i}$

Bemerk dat de vectoren r_i en r'_i alleen een x- en y-component hebben en geen z-component.

Het traagheidsmoment t.o.v. de z'-as is dan:

$I_{z'}=\sum m_{i}{r'}_{i}^{2}=\sum m_{i}({\vec {d}}+{\vec {r}}_{i})\cdot ({\vec {d}}+{\vec {r}}_{i})=(\sum m_{i})d^{2}+2{\vec {d}}\cdot (\sum m_{i}{\vec {r}}_{i})+\sum (m_{i}r_{i}^{2})$

$=(\sum m_{i})d^{2}+\sum (m_{i}r_{i}^{2})$

De term $\sum m_{i}{\vec {r}}_{i}=0$ indien de z-as door het massacentrum gaat. In projectie wordt dit immers $\sum m_{i}x_{i}=mx_{c}=0,\quad \sum m_{i}y_{i}=my_{c}=0$. Dit is typisch als de posities t.o.v. het massacentrum bepaald worden (cfr.supra beweging t.o.v. het massacentrum). De laatste term is het traagheidsmoment t.o.v. deze z-as. De formule wordt dus, met m de totale massa:

$\displaystyle I_{z'}=I_{z}+md^{2}$

Nota: in het Engels is de stelling van Steiner bekend als "the parallel axes theorem".

---

Voorbeelden

Kracht werkend op een wiel

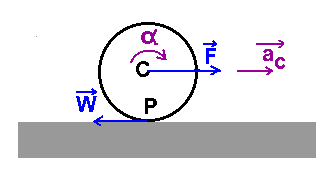
Als 1e voorbeeld wordt een wiel dat rolt zonder slippen behandeld

a. Eerste aanpak: rotatie rond as door massacentrum

De rotatie vergelijking: r.W = I_C.α

Bemerk dat F niet voorkomt in deze vergelijking omdat F door de as wijst en dus geen moment heeft t.o.v. de as. Men heeft nog aanvullende vergelijkingen nodig. Men moet ook de translatievergelijking opschrijven (Wet van Newton):

F - W = m.a_C

Er is een verband tussen a_C en α:

a_C = r.α

Als men het wiel als een volle schijf beschouwt, dan is I_C = m.r²/2

Men krijgt dan als oplossing:

$\alpha ={\frac {2F}{3mr}}$

Bemerk dat er duidelijk wrijving moet zijn om het wiel te doen draaien.

Nota: De wrijving die nodig is om het wiel te doen draaien levert geen energie aan het wiel of onttrekt geen energie eraan. Het punt waarop de kracht werkt staat immers stil (en het komt verticaal toe en vertrekt verticaal, dus loodrecht op de kracht). In de praktijk is er wel energie nodig om iets te doen rollen en weet men dat een hard opgpompte fietsband gemakkelijker rolt dan een bijna platte band. Dit komt omdat er in de praktijk altijd een contactvlak is i.p.v. alleen een contactpunt. Hierdoor zijn er verticale reactiekrachten van de grond die vóór het centrum van het wiel passeren en dus een tegenwerkend moment veroorzaken. Voor een grondiger behandeling, zie "Rollende wrijving" in "Aanvullingen: Wrijving"

b. Tweede aanpak: ogenblikkelijke rotatie rond het contactpunt met de grond

Het contactpunt P met de grond moet dezelfde snelheid hebben als de grond, anders is het wiel aan het slippen. P is dus een stilstaand punt en men kan de beweging ook beschrijven als een ogenblikkelijke rotatie rond P met zelfde α. We moeten nu echter met het traagheidsmoment t.o.v. P werken. Dit wordt berekendwe met de formule van Steiner:

I_P = I_C + m.r² = 3m.r²/2

De rotatie vergelijking wordt nu:

r.F = I_P.α

Dit levert rechtstreeks hetzelfde resultaat.

Bemerk echter dat deze aanpak niet kan gevolgd worden bij een slippend wiel, want dan staat het punt P van het wiel niet stil. De eerste aanpak blijft wel geldig, maar het verband tussen a_C en α vervalt.

Schijf in een lus

Tweede voorbeeld

Als 2e voorbeeld wordt een schijf in een lus van een touw beschouwd.

De beweging wordt beschreven als een beweging van het massacentrum en een rotatie rond een as door het massacentrum. Als men voor de momenten en de hoekversnelling linksdraaiend als positieve zin neemt, dan bekomt men:

r.F - r.S = I_C.α

T.o.v. een as door het middelpunt van de schijf, doet de kracht F de schijf immers naar links en de spanning in het touw de schijf naar rechts draaien. Het gewicht wijst door die as en levert dus geen moment t.o.v. die as. Als de schijf omhoog beweegt, zal de spanning S in het touw kleiner zijn dan F. Er moet immers een netto moment zijn dat linksdraaiend is.

Dit levert 1 vergelijking in 2 onbekenden. Er is nog bijkomende vergelijking nodig. Dit wordt weer de translatievergelijking. Met projectie op een as die omhoog gericht is krijgt men:

F + S - G = m.a_C

Er is een verband tussen a_C en α. Het touw links staat stil. We krijgen dus opnieuw:

a_C = r.α

De oplossing wordt:

$\alpha ={\frac {2(2F-G)}{3mr}}$

Men ziet dat F minstens de helft van het gewicht moet zijn om de schijf omhoog te laten bewegen.

$S={\frac {G+F}{3}}$

Bij F = G/2 is ook S = G/2 en is α = 0: de schijf hangt in evenwicht.

Men zou dit voorbeeld ook kunnen oplossen door de rotatievergelijking op te schrijven t.o.v. het punt waar het touw de schijf raakt, analoog aan de tweede aanpak hierboven. Dat is immers ook een stilstaand punt. Dan zullen F en G voorkomen in de rotatievergelijking, maar S niet.

Afgeleide wetten

Impulsmoment en Behoud van Impulsmoment

Bij translatie kent men grootheid mv die impuls of hoeveelheid van beweging heet. Bij rotatie heeft men een impulsmoment L (in het Engels "angular momentum", in het Duits "Drehimpuls", vandaar in het Nederlands ook soms "draaiimpuls"). Het impulsmoment is feitelijk gedefinieerd als de som van de momenten van de impulsen van alle punten van het voorwerp t.o.v. de rotatieas. Voor een puntmassa m_i geldt dat v_i = r_iω, met r_i de loodrechte afstand naar de rotatieas. Het impulsmoment t.o.v. de rotatieas is dan m_ir_i²ω. Voor het volledige voorwerp krijgt men:

$\displaystyle L_{as}\,=(\sum _{i}m_{i}r_{i}^{2})\omega \,=\,I_{as}\omega$   met zin als  ω

Door de basiswet van de rotatie te integreren in de tijd komt men tot de impulsmomentstelling, die men voor 1 voorwerp kan opschrijven als:

$\int _{t_{1}}^{t_{2}}\sum \mathrm {M_{as}} {\vec {F_{i}}}dt=\Delta \mathrm {I_{as}} .\omega$

waarbij het rechterlid te begrijpen is als de verandering van het impulsmoment, d.i. het impulsmoment op ogenblik t₂ - het impulsmoment op ogenblik t₁.

Voor meerdere voorwerpen moet men alleen rekening houden met de momenten van de uitwendige krachten:

$\int _{t_{1}}^{t_{2}}\sum \mathrm {M_{as}} {\vec {F}}_{i,uitw}dt=\sum \mathrm {I_{as,i2}} .\omega _{i2}-\sum \mathrm {I_{as,i1}} .\omega _{i1}$

Als de som van de uitwendige momenten nul is, dan zal het totale impulsmoment constant zijn. Dit is de wet van behoud va impulsmoment:

$\sum \mathrm {M_{as}} {\vec {F}}_{i,uitw}=0\Leftrightarrow \sum \mathrm {I_{as,i}} .\omega _{i}=constante$

In de praktijk berekent men het impulsmoment op een eerste ogenblik en op een tweede ogenblik en stelt dan dat beide moeten gelijk zijn. Een voorbeeld en tegenvoorbeeld vindt men verder hieronder.

Impulsmoment van een vrij bewegend voorwerp
Als men het impulsmoment moet berekenen van een voorwerp dat rond een bewegende as draait, t.o.v. van een punt P buiten de as door het massacentrum, dan geldt voor een vlak systeem:

L = M_P mv_C + I_C.ω

De eerste term noemt men ook wel het baanimpulsmoment. In sommige landen is dit bekend als de eerste formule van König. Het bewijs ervan kan men hierboven vinden bij de eigenschappen van het massacentrum onder Impulsmoment van een vrij bewegend voorwerp .

Voorbeeld: het impulsmoment van de schijf uit het 2e voorbeeld t.o.v. het bevestigingspunt van het touw:

L = r.mv_C + I_C.ω = 3mr²ω/2

want v_C = rω

Bemerk dat een bewegende puntmassa ook een impulsmoment heeft t.o.v. een bepaald punt of as buiten die puntmassa.
Er bestaat een vrij spectaculaire proef over het behoud van impulsmoment, waarvan men een filmpje kan zien in volgend hoofdstuk onder Behoud van impulsmoment.

Voorbeeld van behoud van impulsmoment

Satelliet

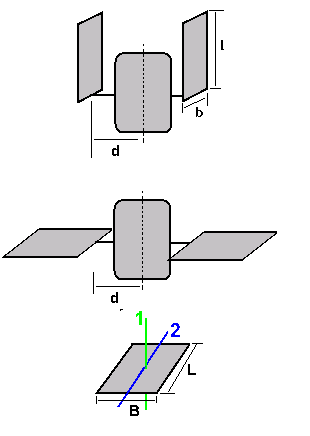
Als voorbeeld bij behoud van impuls beschouwt men een satelliet die uitgezet wordt met een hoeksnelheid ω₀ . De satelliet bestaat uit een centraal deel en twee zonnepanelen. Bij het uitzetten zijn de zonnepanelen opgevouwen langs de satelliet, na het uitzetten worden ze open geplooid. Het centrale deel van de satelliet heeft een gegeven traagheidsmoment I_C, de zonnepanelen hebben een massa m_p en afmetingen l x b.
Alhoewel de satelliet in een baan rond de aarde beweegt onder invloed van de aantrekkingskracht van de aarde, heeft deze aantrekkingskracht geen invloed op de rotatie van de satelliet rond zijn eigen as. De aantrekkingskracht op alle delen van de satelliet kunnen immers vervangen worden door één resultante die aangrijpt in het massacentrum en dat ligt op de rotatieas. Die kracht heeft dus geen moment t.o.v. die rotatieas, m.a.w. heeft geen invloed op de rotatie van de satelliet. De voorwaarde voor behoud van impulsmoment is dus voldaan.

Om het totale traagheidsmoment van de satelliet te berekenen, moet men het traagheidsmoment kennen van een vlakke plaat. Hiervoor zijn echter 2 mogelijkheden:

• ofwel t.o.v. van een as loodrecht op de plaat (as 1 in de figuur), als in de eindsituatie. Dan heeft men: I₁ = m(L² + B²)/12
• ofwel t.o.v. van een as in het vlak van de plaat (as 2 in de figuur), als in de beginsituatie. Dan heeft men: I₂ = mB²/12
  

Er wordt ook weer gebruik gemaakt van de formule van Steiner.

Beginsituatie

I_tot,begin = I_C + 2.(m_p.d²+ m_p.b²/12)

Eindsituatie:

I_tot,einde = I_C + 2.[m_p.(d + l/2)² + m_p.(b² + l²)/12]

Volgens het behoud van impulsmoment moet nu gelden:

I_tot,begin.ω₀ = I_tot,einde.ω_einde

--- Einde voorbeeld ---

Tegenvoorbeeld
Een cilinder A draait rond zijn as met hoeksnelheid ω₀. Een identieke cilinder B die stilstaat wordt tegen deze eerste cilinder geduwd zodat ze beiden uiteindelijk met dezelfde hoeksnelheid ronddraaien. Bereken deze nieuwe hoeksnelheid.

twee cilinders die tegen elkaar draaien

Uit de berekeningen zal blijken dat die eindhoeksnelheid de helft is van ω₀. Men zou dus kennen denken dat er hier behoud van impulsmoment speelt. Maar in de eindsituatie draaien beide cilinders in tegengestelde zin. Hun impulsmomenten moeten dus voorgesteld worden door tegengestelde vectoren waarvan de som 0 is. In het begin was er duidelijk een globaal impulsmoment, op het einde is er geen meer. Er is dus zeker geen behoud van impulsmoment. Er moet dus een uitwendig moment opgetreden zijn dat tegengesteld zin had van het oorspronkelijke impulsmoment van cylinder A.
Opmerking: het impulsmoment van beide cilinders moet in de eindtoestand bepaald worden t.o.v. dezelfde as om over het totale impulsmoment van het systeem te kunnen praten. Om het impulsmoment van de rol B te berekenen t.o.v. de as van de rol A, moet men de hoger gegeven formule L = baanimpulsmoment + I_C.ω gebruiken. Daar het massacentrum van B echter geen snelheid heeft is het baanimpulsmoment = 0 en blijft alleen I.ω_B over. Men kan het vergelijken met het moment van een koppel dat ook onafhankelijk is van het berekeningspunt. Men moet ook bedenken dat de impulsmomentvectoren thuishoren in de ruimte van de momenten, niet in de ruimte van de posities, waarin de rollen getekend zijn.

Om dit alles te begrijpen moet men een krachtenanalyse maken. De 2 cilinders worden iets uit elkaar getekend zodat men duidelijk kan aangeven welke kracht op welk voorwerp werkt. Wanneer de cylinder B tegen cylinder A geduwd wordt, zal deze laatste een kracht F uitoefenen op B. A zelf ondervindt hiervan de reactie. De krachten die door de as van A of B gaan werden niet getekend werden, nl. het gewicht van A en B, de reacties in de lagers en de druk tussen de twee rollen. Deze krachten hebben geen moment t.o.v. die as, m.a.w. ze beïnvloeden de rotatie van de rollen niet.
Men krijgt volgende rotatievergelijkingen, waarbij de positieve zin telkens gekozen werd in de zin van de hoeksnelheid:

• voor A:

$-r.F=I\alpha _{A}$

• voor B:

$r.F=I\alpha _{B}$

Wanneer men lid aan lid optelt en herschikt krijgt men:

$I\alpha _{A}=-I\alpha _{B}$

Men integreert beide leden in de tijd:

$\int _{t_{1}}^{t_{2}}\alpha _{A}.dt=-\int _{t_{1}}^{t_{2}}\alpha _{B}.dt$

$\omega _{A}-\omega _{0}=-(\omega _{B}-0)$

Wanneer op het einde beide cilinders zonder slippen tegen elkaar rollen, is natuurlijk

ω_A = ω_B = ω

Hieruit volgt dan dat ω = ω₀/2

Vanwaar komt nu het uitwendig koppel dat het oorspronkelijke impulsmoment vernietigd heeft? Onder invloed van de kracht F op de cylinder B zou deze naar rechts moeten bewegen. Dat wordt belet door een gelijke maar tegengestelde reactie R_B die aangrijpt op de as van B. Analoog zal er een kracht R_A optreden op de as van A. Deze beide reacties vormen een koppel dat tegengesteld is aan de zin van ω₀. De koppelarm is 2r zodat het moment 2x groter is dan rF en zo het oorspronkelijke impulsmoment teniet doet.

Nota
1. De cilinders moeten in het begin over elkaar slippen. Hierbij gaat energie verloren. De kinetische energie van het systeem is in de eindtoestand dan ook lager dan in de begintoestand:

• Begin: E_k = I.ω₀²/2
• Einde: E_k = 2(I.ω²/2) = I ω₀²/4

2. Als de twee cilinders op één as naast elkaar draaien en zijdelings tegen elkaar gedrukt worden, is er wel behoud van impulsmoment.

--- Einde tegenvoorbeeld ---

Arbeid, potentiële en kinetische energie

Men kan ook een arbeid W berekenen die een moment levert bij verdraaiing van het voorwerp:

$W=\int M.d\theta$

met M = moment van de kracht t.o.v. de rotatieas. Vergeet niet rekening te houden met de zin van moment en hoekverdraaiing. Als ze tegengestelde zin hebben, dan moet één van beide als negatief genoteerd worden. Bemerk ook dat een koppel van krachten geen arbeid levert bij een translatie (de som van beide krachten is 0).

En vermogen wordt dan natuurlijk P = M.ω

Kinetische energie:

- stilstaande as:

$E_{k}={\frac {1}{2}}I\omega ^{2}$

Deze formule volgt onmiddellijk uit:

$E_{k}={\frac {1}{2}}\sum m_{i}v_{i}^{2}={\frac {1}{2}}\sum m_{i}(d_{i}\omega )^{2}={\frac {1}{2}}(\sum m_{i}d_{i}^{2})\omega ^{2}={\frac {1}{2}}I\omega ^{2}$

- bewegende as:

E_k = mv_C²/2 + I_C.ω²/2

Dit is de (tweede) formule van König. De eerste term kan men zien als de bijdrage van de translatie kinetische energie. De afleiding van deze formule werd gegeven onder massacentrum en energie bij het begin van dit hoofdstuk. Alleen werd de kinetische energie van rotatie hier voor een onvervormbaar voorwerp geschreven in termen van ω en het traagheidsmoment.

Hoe kan men beroemd worden met zo'n eenvoudige formule? De uitwerking van (a+b)² levert 3 termen: a² + 2ab + b². Wanneer men de beweging van een voorwerp beschrijft als de beweging van een referentiepunt en een beweging t.o.v. dat referentiepunt, dan zou men in de kinetische energie normaal ook 3 termen aantreffen. Alleen als men als referentiepunt het massacentrum neemt, blijkt dat de kruistermen, van de vorm a.b, wegvallen en alleen de 2 zuivere kwadraten overblijven.

Voorbeeld: kinetische energie van het wiel uit het eerste voorbeeld
De beweging kan op 2 manieren beschreven worden:

• als een samenstelling van een translatie van het massacentrum met een rotatie rond een as door het massacentrum. Dan moet men de formule van König gebruiken met in dit geval I_C = m.r²/2:

E_k = mv_C²/2 + m.r².ω²/4

daar v_C = r.ω wordt dit:

E_k = 3.m.r².ω²/4

• als een zuivere rotatie rond het stilstaande punt P, het contactpunt met de grond. Dan moet men het traagheidsmoment t.o.v. P gebruiken. Dat werd hoger uitgerekend:

I_P = 3.m.r²/2

Hiermede vindt men dadelijk:

E_k = I_P.ω²/2 = 3.m.r².ω²/4

Potentiële energie kan door rotatie opgestapeld worden in bv. een spiraalveer:

E _p= C.θ²/2

met C een veerconstante, maar nu met dimensies Nm/rad

Men ziet dat er een perfect parallellisme is tussen de formules van translatie en rotatie. Samen met de hoger gegeven parallellen, ziet men dat de rol van massa overgenomen wordt door het traagheidsmoment, de rol van de kracht door het moment van de kracht.

Rotatie versus translatie

Er is een eenvoudige proef die op een duidelijk manier het verschil aantoont tussen een translerend en een roterend voorwerp. Bij deze proef wordt een fietswiel bevestigd in een vork die kan slingeren rond een as evenwijdig aan de as van het fietswiel en ongeveer boven het wiel.

Als het fietswiel tijdens het slingeren vrij kan draaien t.o.v. de vork, dan zal het wiel een translatie uitvoeren. Er is immers geen enkel moment dat het wiel een rotatie kan geven. Bij de translatie blijft het onderste punt dus altijd onderaan. Zorgt men dat het wiel niet kan draaien t.o.v. de vork (door een pin tussen de spaken te steken bv.), dan zal het wiel roteren rond het ophangpunt. Bij de rotatie blijft het onderste punt in het verlengde van de vork.

Bij een translatie wordt de beweging beschreven als de beweging van het massacentrum, waaraan het totale gewicht van het voorwerp wordt toegekend. Als het gewicht van de vork verwaarloosbaar is, dan valt dit slingerend wiel in feite onder de formule van de mathematische slinger. Men heeft dus:

$\omega ={\sqrt {\frac {g}{l}}}$

De tijd voor 1 periode is dan:

$T={\frac {2\pi }{\omega }}=2\pi {\sqrt {\frac {l}{g}}}$

Bij de rotatie is het een fysische slinger en moet de bewegingsvergelijking voor een roterend voorwerp gebruikt worden:

$I{\frac {d^{2}\theta }{dt^{2}}}=-r_{C}mg\,\sin \theta$

Met:

I = het traagheidsmoment van de slinger t.o.v.het ophangpunt (eventueel formule van Steiner gebruiken)

r_C = de afstand van het massacentrum tot het ophangpunt

Met de klassieke benadering voor kleine hoeken, waarbij men sin θ = θ stelt, krijgt men een eenvoudige differentiaalvergelijking, die een harmonische beweging voorstelt met

$\omega ={\sqrt {\frac {mgr_{C}}{I}}}$ ...en dat levert normaal een grotere periode.

Men kan beide periodes opmeten en op die manier duidelijk het verschil tussen de translatie- en de rotatiebeweging vaststellen.

Op de foto's is het wiel opgehangen in een vork die gemaakt is uit dunne repen aluminium, in een L-vorm geplooid voor een grotere stijfheid. Deze repen hebben maar een gewicht van 48 g. Dit is verwaarloosbaar t.o.v. 1,935 kg van het wiel zelf, vooral omdat men, voor het geval van een translerend wiel, het traagheidsmoment van deze stroken moet vergelijken met het traagheidsmoment van de totale massa van het wiel beschouwd als geconcentreerd op de as. Dan is de bijdrage van deze stroken minden dan 1%.

Gewicht van het wiel: 1,935 ± 0,003 kg
Afstand tussen as van het wiel en het ophangpunt: 40,8 ± 0,1 cm.

Voor de nauwkeurigheid wordt over verscheidene periodes gemeten (hier 6) en worden de metingen enkele malen herhaald. Dit leverde in dit geval een periode van:

voor de translatie: 1,28 ± 0,02 s

voor de rotatie: 1,53 ± 0,02 s

Dat is een zeer duidelijk verschil!.

De theoretische waarde voor de translatie is:

$\scriptstyle 2\pi {\sqrt {0,408/9,81}}\ =\ 1,28\,\pm \,0,005$ s, pal op de gemeten waarde.

Een theoretische berekening voor de rotatie is niet mogelijk omdat het traagheidsmoment van het wiel t.o.v. de as niet gekend is en niet eenvoudig te bepalen is. De gevonden waarde betekent een traagheidsmoment van het wiel t.o.v. zijn as, dat kan beschreven worden als een massa van 1,4 kg verspreid over de velg van het wiel (r = 31,2 cm). Als men het gewicht van de as (met kogellagers) aftrekt van het gewicht van het wiel, dan moet men inderdaad in de buurt van deze waarde komen.

Gevalstudie: het dynamisch gedrag van een auto

Vertragen en versnellen in rechte lijn

Als toepassing van wat tot nu toe gezien werd, zal het gedrag van een auto bij versnellen en vertragen in rechte lijn en in een bocht bekeken worden. Er wordt uitgegaan van een kleine middenklasse wagen met een massa van 1000 kg, een wielbasis van 2,5 m en aangedreven op de voorwielen. Er wordt gerekend met een (klassieke) gewichtsverdeling van 60% op de voorwielen en 40% op de achterwielen. Het massacentrum bevindt zich op 0,5 m boven de grond.

auto met gegevens

Voor 60% van het gewicht op de voorwielen moet de horizontale afstand van de vooras tot het massacentrum gelijk zijn aan 40% van de wielbasis, d.i. 1 m. De horizontale afstand van massacentrum tot de achteras is dan 1,5 m. Voor de eenvoud wordt g = 10 m/s² genomen (fout kleiner dan 2%). Hiermede wordt het gewicht 10 KN. Hiervan komt dus in rust of bij constante snelheid 6 KN op de vooras en 4 KN op de achteras.

versnellende auto

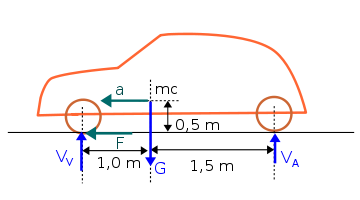
Wanneer de auto versnelt, is er een horizontale kracht F van de grond op de wielen nodig om deze versnelling te veroorzaken. Deze kracht heeft een moment in wijzerzin t.o.v. het massacentrum. Dat moment moet opgevangen worden door een nieuwe verdeling van het gewicht over de verticale reactiekrachten van de grond. Omwille van de elasticiteit van de vering resulteert dat ook in de neus van de wagen die omhoog gaat en de achterzijde die wat daalt. Voor een versnelling van 2 m/s² krijgt men volgende vergelijkingen:
- horizontaal:

$\textstyle F=ma=10^{3}.2=2.10^{3}\ \mathrm {N}$

- verticaal:

$\textstyle V_{V}+V_{A}-G=0$

- momentenvergelijking t.o.v. het massacentrum, positief in wijzerzin:

$\textstyle 1V_{V}-1,5V_{A}+0,5F=0$

Als men de laatste vergelijking van de vorige aftrekt, krijgt men:

2,5V_A = 1G + 0,5F = 10 000 + 1000 = 11 000

Of : V_A = 4 400 N en V_V = 5600 N
In feite moet men eerst de tweede vergelijking met 1 m vermenigvuldigen als men de dimensies wil laten kloppen. Numeriek is dat natuurlijk niet te zien. Er werd toch maar een coëfficiënt 1 voor G gezet.

Er is dus 400 N minder gewicht op de voorwielen en evenveel meer op de achterwielen. Dit is geen gelukkige situatie voor een voorwielaangedreven wagen. De horizontale kracht F moet immers geleverd worden via de wrijving met de weg. Minder druk is op de weg betekent ook kleinere F. Bij de legendarische Citroën Traction Avant (1934) had men het differentieel, vanwaar de aandrijfassen naar de wielen vertrekken, tussen het motorblok en de versnellingsbak geplaatst om meer druk op de voorwielen te hebben. Deze aanpak werd ook gevolgd in de 2CV, de Renault R4 en R5. Alhoewel er reeds in de jaren 30 door DKW gewerkt werd met een dwarsgeplaatste tweetaktmotor, was het vooral de revolutionaire Mini (1959), ontworpen door Alec Issigonis, die de dwarsgeplaatste motor populair maakte. De versnellingsbak zat bij deze in het motorcarter. Bij de huidige wagens is die op zijn normale plaats aan het einde van het motorblok bevestigd. Bij een dwarsgeplaatste motor zit het differentieel naast het motorblok, zo veel mogelijk naar het midden toe. Bij kleinere wagens staat de motor voor de (theoretische) vooras, bij grotere motoren ligt de motor iets schuin over de vooras.

schuin motorblok

motorblok in lijn

Bij het afremmen gebeurt het omgekeerde: de voorwielen worden zwaarder belast en de achterwielen minder. De remkracht moet evenredig hiermede verdeeld worden over de voor- en achterwielen. De remmen op de voorwielen zullen dus altijd het grootste werk moeten. Ze zijn dan ook altijd veel zwaarder uitgevoerd. Bij wagens met schijfremmen vooraan en trommelremmen achteraan is er nog het bijkomende probleem dat de remkracht bij schijfremmen lineair stijgt met de druk op het rempedaal, maar bij trommelremmen eerder exponentieel. In zulk een systeem zit er altijd een begrenzer op de druk naar de achterwielen om het slippen van de achterwielen te vermijden. Deze regelaar of begrenzer wordt meestal gestuurd door de afstand van achteras tot het chassis, als maat voor de helling van de wagen. Bij wagens die met ABS uitgerust zijn moet dat zorgen voor een correcte verdeling van de remkracht.

versnellende auto

Gaat men uit van een vertraging van opnieuw 2 m/s², dan krijgt men volgende vergelijkingen:
- horizontaal:

$F_{V}+F_{A}=ma=10^{3}.2=2.10^{3}\ \mathrm {N} \quad$ maar nu naar rechts gericht.

- verticaal:

$\textstyle V_{V}+V_{A}-G=0$

- momentenvergelijking t.o.v. het massacentrum, positief in wijzerzin:

$\textstyle 1V_{V}-1,5V_{A}-0,5(F_{V}+F_{A})=0$

Men krijgt nu:

2,5V_A = 1G - 0,5.2000 = 10 000 - 1000 = 9 000 N

Of : V_A = 3 600 N en V_V = 6 400 N

Het resultaat is dat de neus van de wagen nu naar beneden duikt.

In de bocht

bovenzicht van auto in bocht met krachten

Wanneer een auto een bocht neemt, dan moet niet alleen het massacentrum een boog beschrijven maar moet ook de wagen gedraaid worden om zijn eigen as. Wanneer de bocht mooi aangelegd is met een constante straal, dan gebeurt dit draaien met constante hoeksnelheid en is er geen moment nodig. Er moeten dan alleen middelpuntzoekende krachten geleverd worden, die zich samenstellen tot één resultante in het massacentrum. De grootte van deze resultante wordt bepaald door de massa van de wagen en de normale versnelling van het massacentrum. Als men onderstelt dat de wagen van hierboven door een bocht gaat met een straal van 125 m aan een snelheid van 90 km/u (= 25 m/s), dan blijkt er een normale versnelling nodig van v²/R = 25²/125 = 5 m/s². Dit vereist een wrijvingscoëfficiënt van 0,5, wat de grens is op een natte baan. Opdat de resultante in het massacentrum zou aangrijpen, moet er weer een 60/40 verdeling zijn over voor- en achterwielen. Voor beide voorwielen is dat dus 3000 N, voor de beide achterwielen 2000 N. Hierbij wordt ondersteld dat alle krachten evenwijdig zijn. Een wielbasis van 2,5 m op een straal van 125 m levert tenslotte maar een hoek van iets meer dan 1°.

Wanneer men hard gaat remmen, kan de situatie kritisch worden voor de achterwielen. Er moet dan immers ook nog een remkracht in de richting van het wiel geleverd worden, terwijl de druk op de achterwielen zal afnemen. Hierboven werd berekend dat bij een afremmen met 2 m/s² de achterwielen een druk van 3600 N zullen uitoefenen.

helling in bocht

Als de remkracht evenredig met de druk over voor- en achterwielen verdeeld wordt, is dit 2000 x (3600/10000) = 720 N voor beide achterwielen samen. Met de middelpuntzoekende kracht van 2000 N wordt dit een totale kracht van $\scriptstyle {\sqrt {2000^{2}+720^{2}}}=2126$ N. Hiervoor is een wrijvingscoëfficiënt nodig van 2126/3600 = 0,59 ! Indien de remverdeling niet optimaal is maar de 60/40 verhouding volgt, zit men aan een wrijvingscoëfficiënt van 0,6. Door hard te remmen verhoogt men dus de kans op uitbreken van de achterwielen. Daarom is de klassieke raad: remmen voor de bocht en eventueel lichtjes accelereren in de bocht. Dit laatste was vooral de raad bij de achterwielaangedreven wagens.

De situatie kan natuurlijk ontmijnd worden door de baan te laten hellen in de bocht. Dan is er een schuine reactie van de grond op de wagen. Bij een juiste keuze van de hoek kan men ervoor zorgen dat de verticale component hiervan het gewicht opvangt en de horizontale de middelpuntzoekende kracht levert. Voor het geval dat hier beschouwd wordt moet de hellingshoek gelijk zijn aan atan(ma/mg) = atan(a/g) = atan(5/10) = 26° 34' . Merk op dat het resultaat onafhankelijk is van de massa van de wagen.

Onderstuur, overstuur en ESP

Wanneer een bocht te snel genomen wordt, dan kan een wagen op twee manieren in de fout gaan. Ofwel breekt de achtertrein eerst uit. Dan gaat de wagen tollen in de zin van de bocht (in de figuur dus rechtsom). De wagen zal dus meer draaien dan nodig is. Daarom noemt men dit gedrag overstuur. Dit is het meest frequente gedrag. Ofwel breken de voorwielen eerst uit. Dan draait de wagen minder dan nodig is. Men noemt dit dan ook onderstuur.

voorbeeld van overstuur en ESP-reactie

Wanneer de achterwielen hun greep op de weg verliezen, zal waarschijnlijk ook de totale wrijvingskracht te klein zijn om het massacentrum in de gewenste baan te houden. De wagen begint dan naar de buitenkant van de bocht te schuiven. Het resultaat is dat een onervaren bestuurder de neiging heeft om de wagen meer naar de binnenkant van de bocht te sturen, dus voor de figuur rechtsom. Daarmee versterkt hij echter nog het tollen van de wagen en loopt de zaak volledig uit de hand. Wat moet gebeuren is tegensturen, d.i. tegen de zin van het tollen van de wagen in sturen, hier dus naar links. Daarmee zal men wel een beetje naar links opschuiven maar het is de enige manier om het tollen te stoppen. Om het eenvoudig te onthouden: als de achterwielen van uw wagen de voorwielen willen voorbijsteken, dan moet je de voorwielen terug voor achterwielen brengen. Of nog: men moet blijven sturen in de richting die men wil volgen.

Vele huidige wagens zijn uitgerust met een elektronisch systeem om het uitbreken te verhinderen. Dit systeem heet "Electronic Stability Program" of kortweg ESP. Dit systeem is gecombineerd met het ABS systeem, dat het slippen van de wielen bij hevig remmen moet vermijden. Het ESP systeem houdt de hoeksnelheid van de wagen continu in de gaten. Wanneer het systeem vaststelt dat de achterwielen willen uitbreken (rode gekromde pijl op de rechtse figuur), zal het de gasklep wat terugdraaien om de snelheid te minderen en het buitenste voorwiel afremmen. Op die manier ontstaat een moment t.o.v. het massacentrum (blauwe gekromde pijl) dat het tollen van de wagen tegengaat en de wagen op de voorzien koers houdt. Eventueel zal men op beide wielen aan de buitenkant van de bocht ingrijpen. Als het tollen veroorzaakt wordt door te hard remmen in de bocht, kan het systeem ook de remdruk op de wielen aan de binnenkant van de bocht verminderen.

Bij onderstuur verliezen de voorwielen hun greep op de weg en zou de wagen op figuur linksom beginnen tollen. In dat geval zal er op het achterwiel aan de binnenkant van de bocht geremd worden om een tegenwerkend moment te veroorzaken.

Door de elasticiteit van de band, treedt er in alle richting een zekere slip op tussen de theoretische en de werkelijke beweging van het wiel. Bij een snel genomen bocht zal het voorwiel niets meer gedraaid zijn dan de weg die het wiel effectief volgt. Dit komt omdat er een klein verschil is tussen de richting van de velg en de richting van het contactvlak met de baan. Bij het sterk versnellen zal de band voor dit contactvlak samengedrukt worden. De velg zal dus iets sneller draaien dan de omtrek van de band. Het omgekeerde gebeurt bij sterk remmen. Dan wordt de band uitgerokken voor het contactvlak en samengedrukt erachter, zodat de velg trager draait dan de omtrek van de band. Het zijn vooral de schommelingen in die slip die de elektronica toelaten om een kritieke situatie te herkennen voor het uit de hand loopt.

Gladde baan

Het is bekend dat een voorwielaangedreven wagen beter onder controle te houden is op een gladde baan dan de normale achterwielaangedreven wagen (er wordt hier niet gesproken over wagens met de motor in het midden). Om dit te begrijpen moet men beseffen dat, bij een achterwielaangedreven wagen, een kracht op de voorwielen in de richting van het wiel (loodrecht op de as), dat wiel alleen maar zal doen draaien maar voor de rest geen invloed heeft op de wagen. Alleen zijdelingse krachten zullen ook op de wagen overgedragen worden. Wanneer, door een ongelijke kracht van de achterwielen, de wagen zich schuin op zijn bewegingsrichting opstelt (zie figuur hieronder, onderste wagen), dan treedt er op elk voorwiel een kracht (paars) op die tegengesteld is aan de snelheid van de auto. Die kan ontbonden worden in een kracht volgens het wiel en een kracht loodrecht op het wiel. Deze laatste versterkt het tollen van de wagen. Door tegen te sturen doet men krachten ontstaan die het tollen tegenwerken (bovenste wagen). Bij een voorwielaangedreven wagen zullen de zijdelingse krachten op de achterwielen het tollen echter tegenwerken.

Slippende auto en tegenstuur