Klassieke Mechanica/Kinematica
De definities[bewerken]
In de kinematica bestudeert men de beweging van een punt door
alleen zijn positie in de loop van de tijd te beschouwen, zonder te zoeken naar de oorzaken van de beweging. De beweging is geheel beschreven als men de positie van het punt kan geven als functie van de tijd. Uit de positie kunnen grootheden als snelheid en versnelling afgeleid worden, die beide in het algemeen ook functies van de tijd zijn. In de kinematica treden dus vooral de volgende grootheden op :
- de positie
- de snelheid: dit is de verandering van de positie als functie van
de tijd, of, meer wiskundig, de afgeleide van de positie naar de tijd.
- de versnelling: de verandering van de snelheid als functie
van de tijd of de afgeleide van de snelheid naar de tijd.
De positie van een bewegend punt kan men echter op verschillende manieren vastleggen en dat geeft aanleiding tot verschillende vormen van "snelheid":
1. Als een punt een baan doorloopt, kan men de positie weergeven m.b.v. de afstand langs de baan voorgesteld door s(t). De grootheid s(t) stelt de afstand tot de positie op het tijdstip t voor, gemeten langs de baan, vanaf een gekozen referentiepunt O. Men moet hierbij nog een positieve richting kiezen voor het doorlopen van de baan. De tegenovergestelde richting is dan automatisch de negatieve richting. Men spreekt in dat geval ook over positieve en negatieve zin voor het doorlopen van de baan. De afstand langs de baan s(t) is een scalaire functie en ook de afgeleiden, zoals snelheid en versnelling langs de baan, zullen scalaire functies zijn. Voor de bepaling van snelheid en versnelling langs de baan hoeft de juiste vorm van de baan niet bekend te zijn.
Door s naar de tijd te differentiëren, krijgt men de snelheid langs de baan:
De afgeleide van deze snelheid levert de versnelling langs de baan:
De index t staat voor "tangentieel" omdat dit alleen de tangentiële component betreft van de versnellingsvector, zoals die hieronder gedefinieerd wordt.
Het aspect richting slaat bij al deze grootheden enkel op de zin die men voor het doorlopen van de kromme gekozen heeft. Zo zal het het teken van de snelheid en versnelling de richting van de beweging langs de baan aangeven, d.w.z.. in positieve of in negatieve zin.
Men heeft maar een beperkte informatie over de drie betrokken grootheden, maar deze is in vele gevallen voldoende.
2. Men verkrijgt alle informatie over de beweging, door de positievector , de plaats in de ruimte op het tijdstip t, als functie van de tijd te geven. De afgeleiden hiervan zullen nu ook vectoriële grootheden zijn. Zo is de snelheidsvector:
en de versnellingsvector:
Om deze formules te gebruiken voor berekeningen, zal men een of ander coördinatensysteem moeten kiezen (cfr. infra).
3. Bij een cirkelbeweging (met straal r) is het voldoende de hoek θ op te geven t.o.v. een referentielijn of -positie om de positie van een punt volledig te bepalen. I.p.v. een lineaire snelheid v krijgt men nu een hoeksnelheid:
en de hoekversnelling:
In de formules waarin θ, ω en α voorkomen moet de hoek in radialen uitgedrukt worden en niet in de meer bekende graden. Radialen zijn de enige coherente eenheid. ω wordt dan radialen per seconde (symbool: rad/s) en α radialen per seconde kwadraat (symbool: rad/s2)
Verbanden[bewerken]
De eerste vraag die hierbij rijst is natuurlijk wat het verband is tussen al deze grootheden.
Er is geen directe relatie tussen s en zelf. Wel blijkt . Hierdoor is er een verband tussen v = ds/dt en = , nl.:
Of: de grootte van de snelheid, berekend uit de positie langs de baan, is ook de grootte van de vectoriële snelheid
Wat de versnelling betreft, blijkt at enkel de tangentiële component van te zijn. Merk op dat |v| en |at| beide de grootte van de tangentiële componenten zijn van vectoriële grootheden. De snelheidsvector is echter zuiver tangentieel, zoals in d volgende paragraaf aangetoond wordt. |v| is dus meteen ook de grootte van . De versnellingsvector kan echter zowel een tangentiële component, at, als een normale component, an, loodrecht op de baan hebben.
Afleidingen[bewerken]
1. De snelheid is altijd rakend aan de baan.
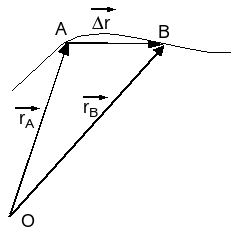
Dit is een zeer belangrijke eigenschap, die eenvoudig aan te tonen is. In de figuur hiernaast kan men zien hoe een punt op een eerste ogenblik t1 in A is en een tijdje later, op t2, in B. De snelheid van dat punt is:
De limietstand van de rechte door 2 punten van een kromme, als die 2 punten naar elkaar toekomen,is de raaklijn. Dus de snelheid ligt volgens de raaklijn.
2. De grootte van de snelheid, berekend uit de positie langs de baan, is ook de grootte van de vectoriële snelheid:
In elk orthonormaal assenstelsel geldt:
Hieruit volgt onmiddellijk:
3. Tangentiële versnelling
Uit beide voorgaande punten blijkt dat de snelheid ook kan geschreven worden als:
Als men deze uitdrukking differentieert naar de tijd krijgt men 2 termen:
De eerste term is een versnelling volgens de raaklijn, nl. de tangentiële versnelling. De tweede term zal de normale versnelling leveren, maar dat wordt verder uitgewerkt na het voorbeeld van de cirkelbeweging.
Eenparige en eenparig versnelde beweging[bewerken]
In de kinematica houdt men zich niet bezig met de oorsprong van de versnellingen. In de dynamica wordt door de wet van Newton een verband gelegd tussen krachten als oorzaak van een beweging en de versnelling. Als men de krachten kent die op een voorwerp werken, kan men zijn versnelling berekenen en zou men door integreren moeten komen tot de snelheid en de positie van dat voorwerp.
Dit "integreren" is echter een beetje sneller gezegd dan gedaan. In de praktijk komt dit neer op het oplossen van een differentiaalvergelijking.
Er zijn echter eenvoudige bewegingen, waarbij dit integreren eenvoudig is. Dit zijn bewegingen zonder versnelling, de eenparige bewegingen, en bewegingen met constante versnelling, de eenparig versnelde bewegingen.
Eenparige beweging[bewerken]
Men spreekt van een eenparige beweging als de beweging met constante snelheid verloopt, dus zonder versnelling. Als er geen versnelling is, moet de snelheid constant zijn. Men vertrekt dan hiervan voor het bepalen van de positie.
1. Als at = 0 is, heeft men een eenparige beweging langs een kromme. Uit v = ds/dt volgt dan:
Hierin is s0 de integratieconstante. Als t=0 staat er dat s(0) = s0. De index 0 (nul) slaat dus, hier en in alle volgende formules op het ogenblik t=0, niet op de oorsprong.
2. Als de vector is, volgt analoog uit
De baan is een rechte lijn gericht langs de snelheid, die vanaf het punt met constante snelheid gevolgd wordt.
3. Als de hoekversnelling α = 0 is, heeft men een eenparige cirkelbeweging met constante hoeksnelheid ω.
Eenparig versnelde beweging[bewerken]
Men spreekt van een eenparig versnelde beweging als de beweging met constante versnelling verloopt. Door integratie kan men formules voor de snelheid en voor de positie afleiden.
1. Als at constant is, volgt uit dv/dt = at dat de snelheid v(t) als primitieve functie moet beantwoorden aan:
en uit v=ds/dt dat:
- ,
2. Als de totale vector constant is (zowel in richting als in grootte!) dan volgt uit :
en uit voor de positie:
waarin de beginpositie (op t=0) en de beginsnelheid is.
De posities vormen een parabool. In drie dimensies ligt die in het vlak bepaald door de beginsnelheid en de versnelling en heeft de richting van de versnelling als symmetrie-as.
Enkel bij rechtlijnige beweging zijn bovengenoemde situaties gelijkwaardig en is zowel de eerste als de tweede reeks formules geldig. In dat geval is er geen normale versnelling, d.w.z.. een versnellingscomponent loodrecht op de baan, en is de tangentiële component ook de totale versnelling. In alle andere gevallen is of at niet constant of is de totale niet constant. Gezien de verbanden tussen deze grootheden is het onmogelijk dat beide constant zouden zijn bij een kromlijnige beweging.
3. Op volledig analoge manier krijgt men voor de cirkelbeweging met constante hoekversnelling α:
en
Remweg[bewerken]
Al deze formules geven snelheid of positie als functie van de tijd. Het is echter interessant om eens te zien hoe de snelheid evolueert in functie van de afgelegde weg. Dit is een toepassing voor de eerste reeks formules. Uit de formule voor de snelheid haalt men de tijd en substitueert die in de uitdrukking voor de afstand s. Dan lost men deze uitdrukking op naar v:
De grafiek hiervan is een liggende parabool. Als het over een vertraging gaat moet a negatief gerekend worden.
Als concrete toepassing wordt het afremmen van een auto bekeken. Onderstelt men een beginsnelheid van 30 m/s (108 km/u) en een vertraging van 5 m/s2, dan bekomt men de grafiek hieronder.

Bij een eenparig vertraagde beweging neemt de snelheid lineair af in de tijd, maar duidelijk niet evenredig met de afgelegde weg. Iedereen die ooit een noodstop heeft moeten uitvoeren aan een grote snelheid, weet hoe men in het begin de indruk heeft dat de remmen niet pakken. Men zou immers een afname willen zien evenredig met de afgelegde weg en dat gebeurt niet. In het begin is de snelheid nog groot zodat er in elke seconde meer weg afgelegd wordt dan op het einde. Als algemene regel geldt dat men steeds driekwart van de stopafstand nodig heeft om de snelheid te halveren. In bovenstaande grafiek is dat 67,5 m.
De stopafstand is de afstand om v=0 te bekomen (met s0=0):
waarbij v0 in m/s moet gegeven worden.
Een eenvoudige formule om de stopafstand te berekenen stelt dat men de snelheid in km/u moet delen door 10 en het resultaat kwadrateren. Bij 100 km/u levert deze formule een afstand van 10 x 10 = 100 m. Uit de bovenstaande formule kan men ook halen met welke vertraging deze formule rekent:
Een vertraging van 5 m/s2 wordt algemeen beschouwd als wat normaal is voor een nat wegdek. In ideale omstandigheden hangt de stopafstand af van het type wagen. Het blijkt dat kleinere wagens nauwelijks 9 m/s2 halen terwijl de zwaardere luxewagens bijna 11 m/s2 kunnen halen. Volgens gegevens van de ANWB heeft een Porsche iets meer dan 36 m nodig om te stoppen vanaf 100km/u (a=10,7 m/s2) en een kleine wagen 46 tot 47,5 m (a<=8,4 m/s2). Het verschil komt vermoedelijk van de bredere banden waarmee zware wagens uitgerust zijn, om de grotere trekkracht van de motor over te brengen zonder de wielen te doen slippen. Deze betere grip op de weg loont ook bij het remmen. Bij een noodstop met een kleine wagen kan men beter een Porsche achter zich hebben dan voor zich! Ook moderne vrachtwagens remmen even kort als personenwagens. Men kan hierover een verrassend filmpje zien op Youtube (zolang het beschikbaar blijft). Men moet echter bedenken dat alle parameters ideaal moeten zijn om deze grote vertragingen te halen: goede droge baan, goede banden met correcte spanning, goed onderhouden remmen.
Een meer nauwkeurige berekening van de stopafstand houdt rekening met een reactietijd van ongeveer 1 s. Als er plots geremd wordt, dan kan de 2e wagen pas reageren als hij de remlichten van zijn voorganger ziet oplichten. Hij moet dat verwerken, wat minstens een halve seconde duurt, en dan nog zijn voet van het gaspedaal naar het rempedaal brengen en dat induwen. Globaal rekent men hiervoor op 1 s. Gedurende die tijd blijft men met constante snelheid bewegen. Men kan zich afvragen of de kleinere vertraging van de simpele kwadratische formule misschien kan compenseren voor het weglaten van die 1e seconde. Het antwoord ziet men in de grafieken hieronder.
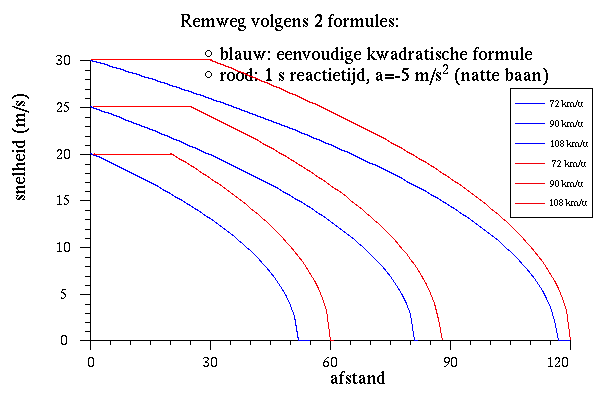
Men kan zien dat de eenvoudige formule bij lage snelheden te optimistisch is op een nat wegdek, rond 100 km/u echter vrij goed is.
Een andere vuistregel zegt dat men 2 s achter zijn voorganger moet blijven, wat ongeveer neerkomt op een aantal meter gegeven door de helft van de snelheid in km/u. Bij 100 km/u wordt dat 50 m, bij 120 km/u 60 m. Om een kop-staartbotsing te vermijden, voor zelfde vertraging van beide voertuigen, moet men minstens een afstand houden die overeenkomt met de afstand die afgelegd wordt tijdens de reactietijd. De "2 seconden regel" is dus aan de veilige kant. Voor een reactietijd van 1 s blijkt er een minimum afstand van 28 m nodig bij 100 km/u en 34 m bij 120 km/u. Rekent men dat de eerste wagen remt met 11 m/s2 en de tweede maar met 9 m/s2, dan worden die afstanden zelfs 36 m en 45 m. Minder dan die afstand achter zijn voorganger hangen is waanzin, of men moet rapper kunnen remmen dan zijn schaduw.
De vectoriële formules[bewerken]
Cartesische coördinaten[bewerken]
Er werd hierboven reeds opgemerkt dat men, om de vectoriële formules te gebruiken voor numerieke berekeningen, moet teruggrijpen naar een of andere coördinatenrepresentatie van de betrokken vectoren. Meest bekend is hier de cartesische voorstelling. Hierbij wordt een onbeweeglijk assenkruis gebruikt. De positievector heeft in 2 dimensies dan coördinaten die we meestal aanduiden met x(t) en y(t) (liever niet rx en ry!), de snelheid krijgt de coördinaten vx(t) en vy(t) en de versnelling krijgt de coördinaten ax(t) en ay(t). Voor de coördinaten van de snelheid gelden de betrekkingen:
en voor de versnelling:
Toepassing: beweging op een cirkel - Normale en tangentiële versnelling[bewerken]
Als toepassing wordt de beweging met constante snelheid van een punt op een cirkel beschouwd. Reeds vroeger, in het deel Elementaire bewerkingen met vectoren, werd aangetoond dat, als een vector constant is in grootte, de afgeleide loodrecht moet staan op die vector. Bij een cirkel is de straal constant en dat is de grootte van de positievector van een punt op de cirkel. De snelheid moet dus loodrecht staan op de positievector. Als de hoeksnelheid voorgesteld wordt door ω worden de projecties van de positievector gegeven door:
Na differentiëren naar de tijd krijgt men voor de snelheid:
Men kan gemakkelijk zien dat inderdaad
De grootte van de snelheid is
Men kan dus besluiten dat als een vector rond draait maar in grootte constant blijft, de afgeleide
- loodrecht staat op de oorspronkelijke vector in de richting van de toename van de hoek
- de grootte van de afgeleide ω maal de grootte van de oorspronkelijk vector is.
Alle eenheidsvectoren zijn voorbeelden van vectoren met een constante lengte. Ze kunnen alleen van richting veranderen, d.w.z. een beetje ronddraaien. Hun afgeleide volgt dus de regels hierboven.
Normale versnelling
Als men nu opmerkt dat ook de snelheid van het punt in dit voorbeeld een vector is die rond draait in de ruimte van de snelheden, dan volgt ogenblikkelijk dat men kan besluiten dat de versnelling van het punt bij constante hoeksnelheid
- zal gericht zijn naar het centrum van de cirkel
- in grootte gelijk zal zijn aan ω2R . Dit is de normale versnelling an.
Indien de hoeksnelheid niet constant is, zal er ook een tangentiële versnelling optreden. Men moet dan in de formules voor de positie de ωt + θ0 vervangen door een θ(t), een willekeurige functie van de tijd. Na een eerste maal differentiëren bekomt men analoge formules als hierboven:
Nu blijft ook ω een functie van de tijd met als afgeleide α. Na nogmaals differentiëren krijgt men:
Men herkent hierin de projecties van 2 vectoriële grootheden:
- at = R.α volgens de raaklijn (en dus ook de richting van de snelheid)
- an = R.ω2 volgens de normaal (naar het middelpunt gericht)
Beide componenten staan loodrecht op elkaar zodat men heeft:
- a2 = ax2 + ay2 = at2 + an2
wat men gemakkelijk kan controleren met de formules hierboven.
Nota: Er is een essentieel verschil tussen een cirkelbeweging en een rotatie. Bij een beweging op een cirkel gaat het over een punt, eventueel een punt van een voorwerp, dat een cirkelbaan volgt. Bij een rotatie gaat het over een voorwerp, waarvan de oriëntatie verandert. Waarschijnlijk staan de meeste elektrische motoren stil. Hun rotor, het draaiend deel ervan, blijft ter plaatse. Het enige verband is dat bij een roterend voorwerp elk punt van het voorwerp een cirkel beschrijft t.o.v. de rotatieas, in een vlak loodrecht op die as (of minstens een stukje van zo'n cirkel). In het hoofdstuk over Dynamica van voorwerpen wordt een proef beschreven die duidelijk aantoont dat bewegen op een cirkel en roteren totaal verschillende zaken zijn. Zie Rotatie versus translatie.
Normale versnelling bij een willekeurige kromme[bewerken]
Hoger werd gezien dat de versnelling kan geschreven worden als:
De eerste term is de tangentiële versnelling. Wat is in de tweede term ?
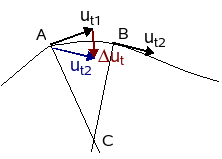
De afgeleide van een eenheidsvector is een vector die loodrecht staat op de oorspronkelijke vector en met grootte ω. De afgeleide van ut is dus een vector die loodrecht staat op deze vector, dus volgens de normaal i.p.v. volgens de raaklijn. Het wordt dus ω.un, met een un die naar de holle kant van de kromme gericht is, zoals blijkt uit de oriëntatie van Δut (zie figuur) en straks uit de zin van ω.
ω is de hoeksnelheid van ut. Hoe kan men die bepalen? Drie punten op een kromme definiëren een cirkel. Als deze 3 punten samenkomen in één punt, dan evolueert deze cirkel naar de raakcirkel of osculerende cirkel. De straal van deze cirkel wordt aangeduid met de Griekse letter ρ (rho) en heet de kromtestraal van de kromme in dat punt. Het centrum van de cirkel is het kromtemiddelpunt. Deze cirkel heeft als eigenschap dat de eerste en de tweede afgeleide in het beschouwde punt dezelfde zijn als van de kromme. Deze cirkel sluit dus veel nauwer aan bij de kromme dan de raaklijn.
Als men de loodlijn trekt op de eenheidsvectoren in A en B, dan snijden die elkaar in C. De hoek θ tussen de eenheidsvectoren ut1 en ut2 is dezelfde als de hoek tussen de normalen in C. Als B steeds dichter bij A gekozen wordt, dan evolueert het punt C naar het kromtemiddenpunt en de afstand AC naar de kromtestraal ρ. In de limiet, als B samenvalt met A, geldt exact dat de snelheid van het punt in A kan geschreven worden als v = ρ.ω, met ω de afgeleide van θ, dus ook de hoeksnelheid van ut. Men heeft dus ω = v/ρ. Invullen in bovenstaande formule levert:
De tweede term is dus de algemene formulering voor de normale versnelling. Men ziet dat de formule een sterke gelijkenis vertoont met de formule voor de cirkelbeweging. Alleen is R nu vervangen door ρ en werkt men liever met de v dan met ω.
Nota: men kan de afleiding wiskundig wat formeel sluitender maken als men beroep doet op één of andere eigenschap van ρ bv. 1/ρ = dθ/ds , maar dan zouden die eigenschappen ook nog moeten bewezen worden.
Valparabool[bewerken]
Wanneer men de luchtweerstand verwaarloost, dan is de valbeweging, het gooien van een steen of bal of het afschieten van een projectiel een eenparigversnelde beweging. Eens het voorwerp aan zichzelf overgelaten is, beïnvloedt alleen de zwaartekracht nog de beweging. Deze zorgt voor een versnelling naar beneden, die onafhankelijk is van de massa van het voorwerp. Deze valversnelling wordt aangeduid met de letter g (van gravitatie) en is in onze streken ongeveer 9,81 m/s2. Voor de praktische berekeningen wordt meestal 10 m/s2 gebruikt, wat een fout is van minder dan 2%. De fout door het verwaarlozen van de luchtweerstand is veel groter.
In vectoriële vorm wordt een valparbool gegeven door:
waarin de beginpositie is (op t=0) en de beginsnelheid is. Bemerk dat er in de vectoriële vorm overal een plusteken staat. De beginsnelheid kan men opschrijven in cartesische coördinaten in een klassiek verticaal-horizontaal assenkruis als (v0x,v0y). Zeer dikwijls wordt echter gewerkt met de grootte en de hoek. Dan worden diezelfde coördinaten geschreven als (v0cos α, v0sin α). Men krijgt dan voor de positie:
Men ziet dat de beweging in de horizontale richting (x-richting) gebeurt met constante snelheid.
Wanneer men de oorsprong van het assenkruis in de beginpositie kan kiezen, verdwijnt de beginpositie uit de vorige formules. Er blijft dan:
- (1)
- (2)
Draagwijdte van een worp
De draagwijdte d wordt bepaald door de plaats waar y opnieuw 0 wordt voor een t verschillend van 0. Men kan dan t wegdelen uit (2), die vergelijking oplossen naar t en die uitdrukking substitueren in (1). Als men dan nog weet dat 2.sin α.cos α = sin 2α dan krijgt men als resultaat:
- (3)
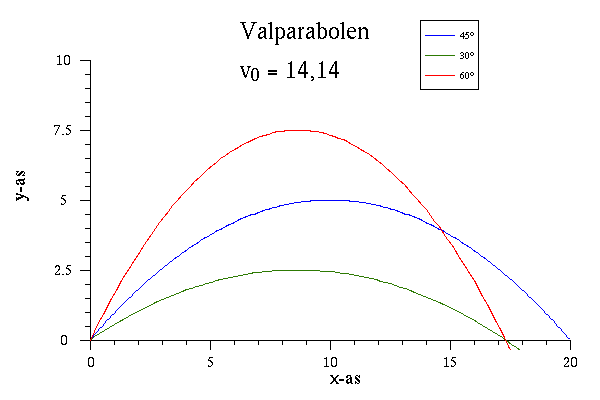
Uit deze formule kan men 2 besluiten trekken:
- De maximale afstand wordt bereikt voor α = 45°. Dan is 2α = 90° en is sin 2α = 1, de maximale waarde voor de sinusfunctie. Deze maximale draagwijdte is dan:
- (4)
- Met een beginsnelheid van 14,14 m/s (=10 x vierkantswortel 2) wordt deze maximale draagwijdte:
- Nota: om een extremum van een functie, een minimum of een maximum, te vinden moet men volgens de algemene theorie het punt zoeken waar de afgeleide van die functie 0 is. Volgens deze aanpak moet men dus (3) afleiden naar α en deze afgeleide gelijk 0 stellen. Uit die vergelijking volgt dan ook dat het maximum bereikt wordt voor 45°.
- Elke kleinere afstand kan bereikt worden door 2 complementaire hoeken. Als men de formule 3 oplost naar α moet men er immers rekening mee houden dat sin 2α en sin (180°- 2α) dezelfde waarde hebben. Dus als sin 2α = 0,5 ,dan zijn de oplossingen 2α = 30° en α=15° en ook 2α=150° en α=75°. Men spreekt van een lage en een hoge parabool waarmede hetzelfde punt kan bereikt worden.

De tijd die nodig is om het eindpunt te bereiken wordt bepaald door de eenparige beweging in x-richting. Als men de hoogte uitzet als functie van de tijd ziet men duidelijk dat de hoge parabool altijd de grootste tijd vraagt.
Hoogste punt
Naast de formules voor de positie zijn er ook nog de formules voor de snelheid. Deze zijn de afgeleiden van (1) en (2) (beginpositie komt er in elk geval niet in voor):
- (5)
- (6)
Het hoogste punt van de parabool wordt bereikt waar vy=0 is. Uit (6) volgt dan dat t=v0sin α/g . Dit invoeren in (2) levert
Het hoogste mogelijke punt bij gegeven v0 wordt natuurlijk bereikt voor α=90° en is
Voor het voorbeeld hierboven krijgt men:
Valparabool 2: hoek, omhullende of veiligheidsparabool[bewerken]
Hoek gevraagd
Wanneer men uit (1) de tijd haalt en die invoert in (2), krijgt men de vergelijking van de baan als y=f(x):
Door beide leden van de identiteit sin2α + cos2α = 1 te delen door cos2α bekomt men een nieuwe identiteit:
Wanneer men dit inbrengt in vorige functie, dan blijkt dit een kwadratische functie in tan α:
- (7)
Deze functie kan men gebruiken om uit te rekenen onder welke hoek men moet gooien of schieten als de coördinaten van het eindpunt en de beginsnelheid gegeven zijn.
Voor de overzichtelijkheid van de volgende afleidingen zullen we stellen:
Hiermede kan de vergelijking herschreven worden in de klassieke vorm voor een kwadratische vergelijking als:
- (8)
Opdat een oplossing mogelijk zou zijn moet de discriminant δ groter zijn of gelijk aan 0:
De grens van het gebied van de punten die kunnen bereikt worden, wordt gegeven door δ=0
Dit blijkt een vergelijking van de vorm y = kwadratische functie in x, m.a.w. een parabool:
Deze parabool noemt men in de ballistiek de veiligheidsparbool (groene stippellijn in de figuur hieronder).
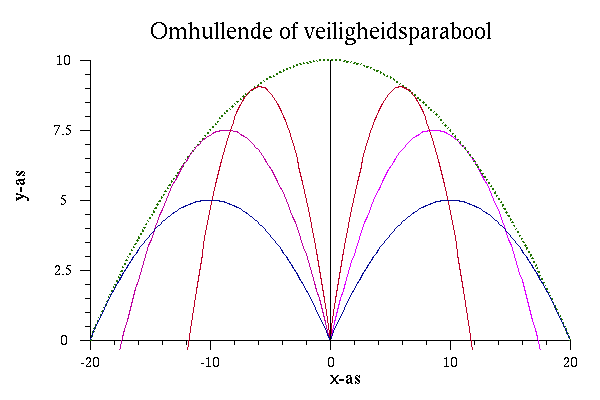
De snijpunten met de assen:
- snijpunten met x-as voor y=0: x = ±v02/g
Voor het voorbeeld hierboven: x = ±200/10 = 20 m ... zoals hierboven gevonden
- top: y = v02/2g
Voor het voorbeeld hierboven: y = 200/20 = 10 m ... zoals hierboven gevonden
Er is nog een andere manier om tot deze parabool te komen. Als men een reeks krommen kan genereren door een parameter te wijzigen, dan kan die familie krommen een omhullende hebben. Deze omhullende is een kromme zodanig dat
- door elk punt van de omhullende één kromme van de familie passeert
- de raaklijn in dat punt aan die kromme en aan de omhullende samenvallen.
Om deze omhullende te vinden moet men de vergelijking van een kromme afleiden naar de parameter, deze afgeleide = 0 stellen en de parameter elimineren tussen deze vergelijking en de oorspronkelijke vergelijking voor de kromme. Hier zou men α als parameter kunnen beschouwen in (7), maar men kan evengoed tan α als parameter nemen. Men krijgt dan als 2e vergelijking door afleiden van (8):
Dit oplossen naar tan α en substitueren in (8) levert opnieuw de vergelijking van de veiligheidsparabool.
Valparabool 3: maximale afstand op helling, luchtweerstand[bewerken]
Maximale afstand op een helling
Als men de vraag stelt onder welke hoek men moet schieten om een pijl zo ver mogelijk op een helling te laten neerkomen, is dit een probleem dat sterk verschilt van het bepalen van de maximale horizontale reikwijdte. Zij β de hoek van de helling met de horizontale en d de gezochte maximale afstand. Men kan de vectoriële formule
nu projecteren op een klassiek verticaal-horizontaal assenkruis of op een schuin assenkruis.
1. In een klassiek verticaal-horizontaal assenkruis
Hierbij moet de hoek tegenover een horizontale x-as uitgedrukt worden:
Uit de eerste vergelijking haalt men de tijd en substitueert die in de tweede. Na heel wat rekenwerk en toepassen van goniometrische som- en verschilformules kan dit herwerkt worden tot:
Deze uitdrukking moet men nu partieel differentiëren naar α en deze afgeleide = 0 stellen:
Of cos(2α + β) = 0
Dit heeft als oplossing 2α + β = 90° of
- t.o.v. de helling.
Voor een helling van 20° krijgt men als optimale hoek: α = 45° - 20/2 = 35° t.o.v. de helling of 35° + 20° = 55° t.o.v. de horizontale.
2. In een schuin assenkruis
De x-as wordt langs de helling gelegd en de y-as staat daar loodrecht op. In eerste instantie krijgt men hier een complicatie omdat de valversnelling g nu 2 componenten heeft en moet geschreven worden als (-g.sinβ, -g.cosβ). Het blijkt echter dat de verdere uitwerking eenvoudiger uitvalt doordat men nu opnieuw kan stellen dat y=0 is in het eindpunt. De hoek α is nu de hoek met de x-as.
In de laatste vergelijking kan t eenmaal weggedeeld worden, waarna men hieruit t haalt en substitueert in de eerste vergelijking. Dit levert uiteindelijk:
Partieel differentiëren en het resultaat = 0 stellen leidt tot
en zo opnieuw tot cos(2α + β) = 0 zoals bij de vorige aanpak.

Nota: didactisch belang
Didactisch gezien zijn valparabolen een interessante topic. De theorie bevat 2 vectoriële vergelijkingen (voor snelheid en positie) in 1 scalaire variabele (de tijd) en 4 vectoriële variabelen: . Voor het tweedimensionale geval levert dit 4 vergelijkingen in 9 veranderlijken. Van die 9 moeten er dus 5 gegeven worden, de andere 4 kan men dan uitrekenen. Dit geeft de mogelijkheid om een zeer grote verscheidenheid aan vraagstellingen te maken. Hierdoor is het niet mogelijk om pasklare formules te maken voor elke situatie, maar moet men leren van basisformules te vertrekken en die om te werken volgens de vraag van het ogenblik.
3. Luchtweerstand
De beschrijving van de valparabool, zoals hierboven gegeven, houdt geen rekening met de luchtweerstand. Een werkelijke worp verloopt dus anders. De oplossing voor de beweging met luchtweerstand is spijtig genoeg niet eenvoudig. Men moet dan vertrekken van een toepassing van de wet van Newton van de vorm:
In woorden: de versnelling wordt bepaald door de aantrekkingskracht van de aarde en door een tegenwerkende kracht die afhankelijk is van de snelheid en tegen de snelheid in gericht is. De horizontale snelheid wordt nu ook vertraagd door die luchtweerstand. Daardoor is de baan geen parabool meer. Men kan een gebied onderscheiden van lage snelheid waarin de weerstand evenredig is met de snelheid. Dit levert nog een eenvoudige differentiaalvergelijking. Bij een penalty schot of bij tennis of golf zijn de snelheden echter te hoog voor deze eenvoudige formules. Men komt dan in een gebied waar de weerstand evenredig is met het kwadraat van de snelheid. Dit geeft een veel ingewikkelder differentiaalvergelijking. De speciale oppervlakte structuur van een golfbal of de donzige bekleding van een tennisbal zorgen voor complexe fenomenen die als gevolg hebben dat de luchtweerstand bij hoge snelheden vermindert. Wie hierover meer wil weten kan zijn zoektocht beginnen met de paragraaf over viskeuze wrijving
4. Simulaties
Nota: sinds begin 2017 ondersteunen veel browsers geen Java meer. Daardoor kunnen veel applets niet meer uitgevoerd worden in een browser. Sommige auteurs hebben hun applets omgewerkt naar HTML5, zoals bv. Walter Fendt. HTML5 zou op alle media (pc's, tablets, smart phones) moeten werken. Een andere mogelijkheid is het applet omvormen tot een zuiver Java programma, dat men dan moet downloaden en uitvoeren op zijn computer m.b.v. de "Java run time engine"(JRE). Op https://www.walter-fendt.de/ph14d/ worden beide mogelijkheden aangeboden. De onderstaande links verwijzen naar simulaties die geen Java applets zijn.
Er zijn veel applets beschikbaar over de valparabool zonder luchtweerstand.
Schuine worp zonder luchtweerstand (Flash)
Uit de boom vallende aap raken Klein spelletje!
Voor wie zelf wat wil experimenteren kan dat met elk programma dat toelaat een willekeurige functie van de vorm y=f(x) te plotten.
Poolcoördinaten[bewerken]
Het assenkruis voor snelheid en versnelling[bewerken]
Een andere voorstelling in twee dimensies, die voor de technische toepassingen zeer dikwijls interessanter is, is door middel van poolcoördinaten. Na de keuze van een referentiepunt, de pool, en een referentierichting, wordt de positie weergegeven door een koppel van twee parameters: de afstand r tot de pool en de hoek θ tussen de voerstraal en de referentierichting. De afstand r is hier een strikt cartesische afstand, dus nooit negatief. Er moet een positieve zin afgesproken worden voor θ. Dit is meteen ook de positieve zin voor de afgeleiden van θ. Dikwijls kiest men hiervoor de draairichting linksom, de tegenwijzerzin, de richting tegen de klok in, omdat dat overeenkomt met de positieve zin in een tweedimensioneel cartesisch assenkruis met x-as naar rechts en y-as omhoog. Dit is echter geenszins verplicht en men mag de zin kiezen die het best bij de gegeven situatie past. B.v. bij het probleempje van de auto die een brug oprijdt juist op het ogenblik dat die begint te draaien (cfr.infra), is het logisch om de zin van de hoekversnelling van de brug als positieve zin te nemen.
Merk op dat r en θ geen componenten zijn van een vector.

De snelheid en de versnelling worden wel op de gebruikelijke manier als vector beschreven. Deze componenten worden beschouwd t.o.v. een assenkruis waarvan
- de oorsprong normaal in het beschouwde punt gekozen wordt;
- de r-as wijst in de richting van toenemende r (dus steeds van de pool weg)
- de θ-as staat loodrecht op de r-as, 90° gedraaid in de
zin van toenemende θ (of: in de positieve zin voor θ )
De componenten van de snelheid zijn (de afleidingen zullen later toegevoegd worden):
- : de radiale component
- : de transversale of θ component.
Bemerk dat beide gewone snelheden zijn, die in m/s uitgedrukt worden. In het voorbeeld hierboven is vr positief maar vθ negatief.
Men kan gemakkelijk de betekenis zien van de termen: vr is de snelheid van de radiale verplaatsing, vθ komt overeen met de omtreksnelheid van een punt op een cirkel met straal r.
De componenten van de versnelling:
en
Bemerk dat men op niveau snelheid telkens 1 term heeft voor elke component en op niveau versnelling telkens 2 termen. De betekenis van de versnellingstermen is ook eenvoudig: ar bestaat uit de versnelling van de radiale verplaatsing + de normale versnelling van de cirkelbeweging. aθ bestaat uit wat de tangentiële versnelling zou zijn bij een cirkelbeweging en een speciale term die verder verklaard wordt.
Afleiding van de formules[bewerken]
Men kan de positie van een punt beschrijven als:
Er zal nu beroep gedaan worden op wat hoger in de bespreking van de cirkelbeweging aangetoond werd, nl.dat de afgeleide van een eenheidsvector loodrecht staat op die vector in de richting van toenemende hoek en ω maal de vector is. Dat levert hier:
Hiermede vallen de snelheid en versnelling eenvoudig uit te rekenen:
En analoog voor de versnelling:
Na invullen van de uitdrukkingen voor de afgeleiden van de eenheidsvectoren en hergroeperen krijgt men:
Praktisch gebruik van poolcoördinaten[bewerken]
Voor het bepalen van de radiale en transversale componenten van snelheid en versnelling bij gebruik van poolcoördinaten r en θ speelt de hoek θ zelf geen rol. Wel de voerstraal r, en van beide parameters de eerste en tweede afgeleide. De voorkomende grootheden zijn dus:
Wanneer men snelheid en versnelling in poolcoördinaten moet gebruiken, moet men dus beginnen met zich eerst af te vragen wat men over deze 5 grootheden weet. Als men voor deze elementen numerieke waarden kent, dan kan men alle componenten van snelheid en versnelling berekenen en indien nodig de versnelling ook omrekenen naar normale en tangentiële versnelling.
Voorbeeld

Nemen we als voorbeeld het probleem van de auto op de brug. Op het ogenblik
dat een auto een brug oprijdt, begint deze te draaien met een hoekversnelling van 1/6 rad/s2 De snelheid van de auto op de brug is 5 m/s . Bereken de snelheid en versnelling van de auto als de auto 15 m ver is op de brug.
Dit is een goed probleem voor poolcoördinaten omdat de beweging een combinatie
is van een draaiende drager met daarop een beweging door het centrum van de
rotatie (radiale beweging). Als pool moeten we een stilstaand punt hebben. Dat
wordt dus het midden van de brug. Als positieve zin voor de hoekgrootheden kiezen we de zin van de hoekversnelling α, wijzerzin dus.
Wat weten we over de 5 basiselementen?
r = 15 - 11 = 4 m voorbij 't midden.
vr = +5 m/s (snelheid van de wagen op de brug, volgens de positieve
zin van de r-as)
De afgeleide, d2r/dt2, hiervan is nul daar vr constant is.
De hoeksnelheid ω is niet rechtstreeks gegeven, wel de hoekversnelling
α . ω moet dan volgen uit de betrekking: ω(t) = ω0 + αt = 0 + 1/6 x 3 = ½ rad/s
α = 1/6 rad/s2.

Hieruit volgen dan door eenvoudig invullen in de formules van poolcoördinaten
de verschillende componenten van snelheid en versnelling:
vθ = r. ω = 4.1/2 = 2 m/s
ar = d2r/dt2 - r.ω2 = 0 -
4.(1/2)2 = -1 m/s2
aθ = r.α + 2.vr.ω =
4.1/6 + 2.5.1/2 = 5 2/3 m/s2 = 5,667 m/s2
Snelheid en versnelling staan bijna loodrecht op elkaar. Met de formules hieronder zal men een grote normale versnelling en een kleine tangentiële versnelling bekomen.
De meest voorkomende fout is dat men een functie maakt voor de positie van de
auto op de brug:
r = 11- v.t want op t = 0 moet r = 11 m zijn.
Voor t = 3 levert deze functie echter een negatieve waarde voor r, nl. - 4 m,
wat onaanvaardbaar is. Deze functie is enkel geldig vóór de auto het midden
van de brug bereikt heeft. Eens de wagen voorbij het midden is moet men schrijven r = v.t - 11.
Bemerk dat de eerste functie voor vr de waarde -5 m/s levert. Dit is de correcte waarde vooraleer de auto het midden bereikt. Controleer
dit door het assenkruis te tekenen als de wagen nog voor het midden is! (r-as
moet naar buiten wijzen, vr is naar het centrum van de brug)
De term 2.vr.ω[bewerken]
De fysische betekenis van deze term kan gemakkelijk worden aangetoond. Hij treedt alleen op als iemand zich in een draaiend systeem bevindt EN zijn afstand tot het rotatiecentrum verandert. Dit is feitelijk een vorm van Coriolisversnelling.

Kijken we hiervoor naar de figuur hiernaast. Als iemand in het punt P1 staat (afstand r1), dan heeft hij een omtreksnelheid vθ1. Als hij in P2staat (afstand r2) heeft hij een evenredig grotere omtreksnelheid vθ2.
Veronderstellen we nu dat iemand op het ogenblik t0 in P1 vertrekt en met een constante vr naar P2 marcheert. Na een tijd Δt komt hij dan in P2 . Doordat zijn afstand tot
het rotatiecentrum van r1 toegenomen is tot r2, is zijn
omtreksnelheid toegenomen van vθ1 tot vθ2
. Voor deze toename met Δvθ is er een versnelling in de
richting van vθ nodig geweest. Voor constante vr
en ω kan deze berekend worden als
Δvθ/Δt = ((r2 - r1)*ω)/((r2 - r1)/vr) = vr*ω
Dit is dus het effect van de verandering van r.
Als de man van buiten naar binnen komt, moet vr negatief gerekend worden en wordt deze term negatief. De omtreksnelheid van de man moet dan kleiner worden, hij moet afgeremd worden. Hiervoor is een versnelling nodig die tegengesteld is aan vθ .
De term vr*ω komt echter nog een tweede maal voor. Op het ogenblik dat de man in P2 toekomt, zal het systeem gedraaid zal zijn t.o.v. de vertrekpositie. Op dat ogenblik marcheert de man niet meer in de oorspronkelijke richting van P2, maar misschien in de richting van P'2. De richting van vr verandert dus voortdurend. Ook dit vraagt een versnelling loodrecht op vr en gelijk aan vr*ω (de top van vr beschrijft een cirkel in de ruimte van de snelheden). Zo komt men aan 2*vr*ω.
Normale en tangentiële versnelling[bewerken]
De versnelling kan niet alleen ontbonden worden in componenten volgens verschillende assenkruisen, ze kan ook ontbonden worden in een normale en tangentiële component. De tangentiële component is rakend aan de baan, parallel met de snelheid. De normale component is gericht naar het kromtemiddenpunt van de baan. Hieronder volgt een overzicht van de formules om van een de componenten in een orthogonaal assenkruis over te gaan naar normale of tangentiële versnelling.
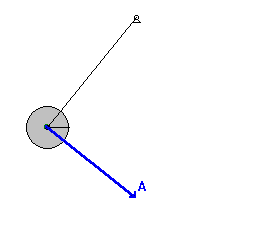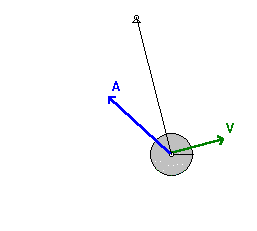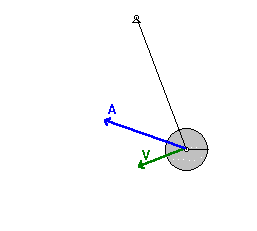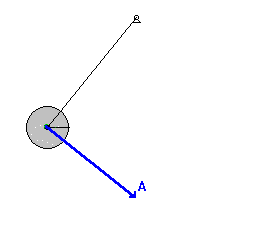
In de uiterste standen van de slinger is er alleen een tangentiële component at van de versnelling en in de laagste stand alleen een normale component an.
Tangentiële versnelling[bewerken]
1 - Volgens de definitie:
In 2 dimensies kan hiervoor geschreven worden:
Alhoewel de richting van de assen veranderlijk is bij poolcoördinaten, mag deze formule ook gebruikt worden met poolcoördinaten omdat de grootte van een vector een invariant is voor rotatie.
2 - Door projectie op de raaklijn aan de baan
De tangentiële component van de versnelling is de projectie van de versnelling op de raaklijn aan de baan, die gegeven is door de snelheid. De projectie kan men bepalen door het scalaire product van de versnelling met een eenheidsvector volgens de raaklijn. Die kan men construeren door de snelheid te delen door de norm ervan. In een orthogonaal assenkruis is een scalair product eenvoudig uit te rekenen.
Dit is een interessante formule wanneer de componenten van a en v al bekend zijn in een orthogonaal assenkruis. De formule is ook bruikbaar voor numerieke waarden op een bepaald ogenblik. En als in twee dimensies een van de componenten van a of v nul is, staat er in de teller nog hoogstens één term.
3 - Volgens de stelling van Pythagoras:
4 - Voor een cirkelbeweging:
Normale versnelling[bewerken]
1 - Volgens de definitie:
waarin ρ de kromtestraal van de baan in het beschouwde punt is. Voor een cirkel is dat de straal r. Deze betrekking wordt echter meestal gebruikt om ρ te bepalen, waarbij an via een andere weg bekend moet zijn.
2 - door projectie op de normaal
De normaal is een eenheidsvector loodrecht op de snelheid. Voor de projectie op de normaal moet men a vermenigvuldigen met de sinus van de hoek tussen snelheid en versnelling. Deze sinus kan men uit het vectoriëel product halen gedeeld door de norm van a en v. Hierdoor valt a onder en boven weg. In een vlak systeem heeft dit vectoriëel
product maar één component, die men dan ook gemakkelijk kan uitschrijven:
De indices 1 en 2 mogen vervangen worden door x en y of door r en θ. Dit is weer een zeer interessante formule om dezelfde redenen als vermeld bij de tangentiële versnelling.
3 - Volgens de stelling van Pythagoras:
4 - Voor een cirkelbeweging:
Steeds geldt volgens de stelling van Pythagoras:
Dit kan men eventueel als controle gebruiken bij het omrekenen. De grootte van de versnelling moet dezelfde blijven, in welke coördinaten die ook uitgedrukt wordt.
Voorbeeld[bewerken]
Toegepast op het voorbeeld van de auto op de brug met in poolcoördinaten
v(5; 2) en a(-1; 5,667), telkens met de 3e formule:
(i lopend over r en θ)
(met index 1 = r en index 2 = θ )
Ter controle: de grootte van a moet in alle ontbindingen dezelfde zijn:
O.K.

Bemerk dat het kromtemiddelpunt van de baan in de richting van an
ligt, niet in het midden van de brug.








































































































