Elektronica/Logische Basispoorten
Logische basispoorten[bewerken]
Inleiding[bewerken]
In dit onderdeel zullen de meest voorkomende basis logische poorten (dit zijn blokken die een logische functie realiseren waarvan de uitgang enkel afhangt van de ingang) aanraken. In dit onderdeel zal enkel gebruik gemaakt worden van de positieve logica, dus waar een logische 1 voorgesteld zal worden door een 1 en een logische 0 zal voorgesteld worden door een 0 (alternatieven zijn hoog/laag, waar/vals, ...). Elke logische poort zal op vijf verschillende manieren geïllustreerd worden:
- Via een waarheidstabel die ingangen mapt op uitgang
- Via het IEC (International Electrotechnical Commission) symbool
- Via het ANSI symbool (welke het meest frequent gebruik wordt in Amerikaanse databladen)
- Via het DIN (Deutsche Institut für Normung) symbool
- Via diens logische functie.
Alle poorten zullen in hun eenvoudigste mogelijke vorm geïllustreerd worden, zo zijn bvb EN poorten met meerdere ingangen mogelijk maar twee ingangen volstaat om het principe te illusteren. De ingangen zullen A en B (indien aanwezig) heten, de uitgang Q
Buffer[bewerken]
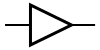
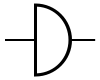
De buffer geeft op de uitgang wat op de ingang aanwezig is.
Waarheidstabel[bewerken]
| A | Q |
|---|---|
| 0 | 0 |
| 1 | 1 |
Symbolen[bewerken]
| IEC | ANSI | DIN |
|---|---|---|
 |
 |
|
Logische vergelijking[bewerken]
NIET-poort (NOT)[bewerken]
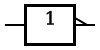
De NIET-poort is de inverse functie van de buffer.
Waarheidstabel[bewerken]
| A | Q |
|---|---|
| 0 | 1 |
| 1 | 0 |
Symbolen[bewerken]
| IEC | ANSI | DIN |
|---|---|---|
 |
 |

|
Logische vergelijking[bewerken]
EN-poort (AND)[bewerken]
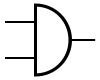
De EN-poort geeft enkel 1 als alle ingangen 1 zijn; in andere gevallen is de uitgang 0
Waarheidstabel:[bewerken]
| A | B | Q |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Symbolen:[bewerken]
| IEC | ANSI | DIN |
|---|---|---|
 |
 |
|
Logische vergelijking[bewerken]
NEN-poort (NAND)[bewerken]
De NEN-poort geeft enkel 1 indien minstens één ingang 0 is, dit is de inverse van de EN-poort.
Waarheidstabel:[bewerken]
| A | B | Q |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Symbolen:[bewerken]
| IEC | ANSI | DIN |
|---|---|---|
 |
 |

|
Logische vergelijking:[bewerken]
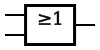
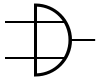
OF-poort (OR)[bewerken]
De OF-poort geeft enkel 1 indien minstens één ingang 1 is.
Waarheidstabel:[bewerken]
| A | B | Q |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Symbolen:[bewerken]
| IEC | ANSI | DIN |
|---|---|---|
 |
 |
|
Logische vergelijking:[bewerken]
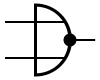
NOF-poort (NOR)[bewerken]
De NOF-poort geeft enkel 1 indien geen enkele ingang 1 is. Dit is de inverse van de OF-poort.
Waarheidstabel:[bewerken]
| A | B | Q |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Symbolen:[bewerken]
| IEC | ANSI | DIN |
|---|---|---|
 |
 |
|
Logische vergelijking:[bewerken]
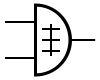
Exclusieve OF-poort (EXOR)[bewerken]
De exclusieve OF-poort (EXOF) geeft 1 indien exact één ingang 1 is. Noot: Bemerk dat wanneer men in de dagelijkse omgang het woord of gebruikt dit typisch in deze exclusieve context gebruikt wordt. In een restaurant kan men kiezen uit schotel nummer 1 OF schotel nummer 2 voor een bepaald bedrag. Indien men dan de logische of zou gebruiken zal de eigenaar dit niet appreciëren.
Waarheidstabel:[bewerken]
| A | B | Q |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Symbolen:[bewerken]
| IEC | ANSI | DIN |
|---|---|---|
 |
 |
|
Logische vergelijking:[bewerken]
Exclusieve NOF-poort (EXNOR)[bewerken]
De exclusieve NOF-poort (EXNOF) geeft 1 indien beide ingangen gelijk zijn aan elkaar. Dit is het inverse gedrag van de exclusieve OF-poort.
Waarheidstabel:[bewerken]
| A | B | Q |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Symbolen:[bewerken]
| IEC | ANSI | DIN |
|---|---|---|
 |
 |

|
Logische vergelijking:[bewerken]
NAND logica[bewerken]
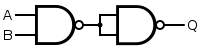
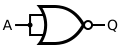
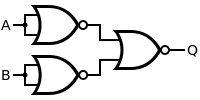
Praktisch gezien kan men bij het bekijken van bovenstaande waarheidstabellen concluderen dat een aantal poorten overbodig zijn. Zo kan men bijvoorbeeld stellen dat XNOR perfect kan uitgedrukt worden in functie van NIET-, OF- en EN-poorten: De hierboven gebruikte vorm heet de disjunctieve normaalvorm, maar hierover later meer. Nu is het zo dat men in een productieproces bij voorkeur maar één type poort gaat gebruiken. Zo kan men aantonen dat men elke logische functie kan bekomen louter door gebruik te maken van NEN- en NOF-poorten. Zo is de NIET poort niets anders dan een NEN-poort waarvan de ingangen met elkaar verbonden zijn. Vervolgens kan men zo makkelijk een EN en een OF poort maken:
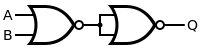
Hetzelfde is mogelijk met louter NOF-poorten:
Productterm[bewerken]
Gegeven een logische functie van n veranderlijken (A tem N) dan is een productterm een willekeurige combinatie van een aantal logische veranderlijken (al dan niet gecomplementeerd) gecombineerd met een logische EN-functie. Voorbeelden zijn: .
Somterm[bewerken]
Gegeven een logische functie van n veranderlijken (A tem N) dan is een somterm een willekeurige combinatie van een aantal logische veranderlijken (al dan niet gecomplementeerd) gecombineerd met een logische OF-functie. Voorbeelden zijn: .
Standaardproduct[bewerken]
Een standaardproduct is een productterm waarin elke logische veranderlijke voorkomt. In geval van een functie met vier logische veranderlijken zijn volgende uitdrukkingen voorbeelden van standaardproducten: . Een logische functie van n veranderlijken heeft dus een standaardproduct dat uit n factoren bestaat.
Disjunctieve normaalvorm[bewerken]
Een disjunctieve normaalvorm (Disjunctive Normal Form of DNF) van een logische functie is deze logische functie herschreven als een somterm van standaardproducten waarvoor deze logische functie waar is. Deze kan makkelijk geconstrueerd worden vertrekkende van de waarheidstabel, zo werd eerder reeds geïllustreerd wat de disjunctieve normaalvorm was van de XNOF-poort. Een disjunctieve normaalvorm kan zo maximaal uit 2n termen bevatten van standaardproducten die op hun beurt uit n factoren bestaan.
Praktische toepassing in PALs[bewerken]
PAL (Programmable Array Logic) zijn een familie halfgeleiders die toestaan om een willekeurige logische functie te programmeren, hiervoor bestaan verscheidene technologieën waarvan PROM (Programmable Read Only Memory) er één van is. Een simpele voorstelling van een PROM chip is te zien in volgend schema:
Links bevinden zich twee ingangen (de redenering laat zich makkelijk uitbreiden naar n ingangen en m logische functies), van deze ingangen worden net als hun inverse via een zekering verbonden met een EN-poort (elke EN poort heeft ingangen). Door zekeringen te vernietigen (tijdens het programmeren) kunnen zo standaardproducten geprogrammeerd worden, de uitgangen van de EN-poorten worden verbonden met een OF poort met meerdere ingangen, het aantal EN-poorten (en dus ook het aantal ingangen van de OF-poort) bepaalt het aantal standaardproducten welke een 1 als resultaat kunnen hebben. Het is duidelijk dat dit een directe toepassing is van de disjunctieve normaalvorm.
In GALs (Generic Array Logic) kunnen meerdere logische functies tegelijk gerealiseerd worden, daar deze uit een configureerbare EN- en een configureerbare OF-matrix bestaan. Alhoewel er ook PALs bestaan die deze functionaliteit voorzien.